高中数学选修2-2课件1_7 定积分在几何中应用（1） 12页

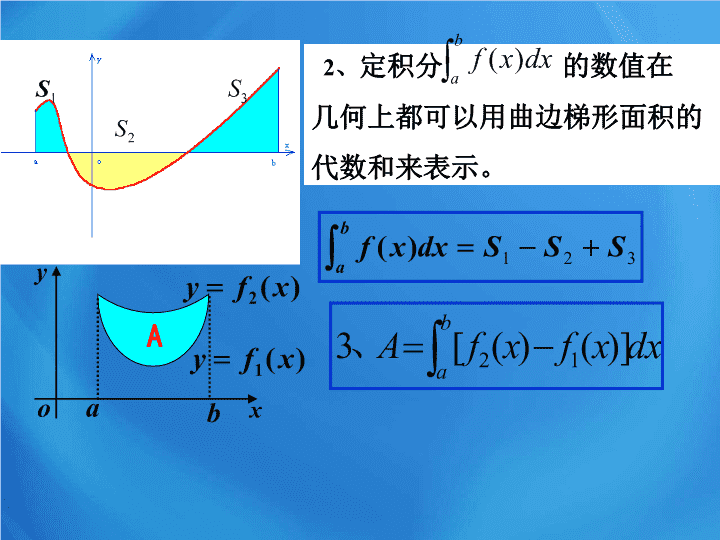
1.7.1 定积分在几何中的应用 定积分的简单应用： 一 . 定积分的几何意义是什么？ A 1 、 如果函数 f （ x ）在 [a ， b] 上连续且 f （ x ）≥ 0 时，那么： 定积分 就表示以 y=f （ x ）为曲边的曲边梯形面积 。 曲边梯形的面积 复习引入 曲边梯形的面积的负值 2 、 定积分 的数值在 几何上都可以用曲边梯形面积的 代数和来表示。 A 二、 微积分基本定理内容是什么？ 设函数 f ( x ) 在区间 [ a,b ] 上连续，并且 F’(x) ＝ f （ x) ，则， 这个结论叫 微积分基本定理 （ fundamental theorem of calculus) ，又叫 牛顿－莱布尼茨公式 （ Newton-Leibniz Formula). 解 : 作出 y 2 =x,y=x 2 的图象如图所示 : 即两曲线的交点为 (0,0),(1,1) o x y A B C D O 直线 y=x-4 与 x 轴交点为 (4,0) 解 : 作出 y=x-4, 的图象如图所示 : S 1 S 2 点评： 求两曲线围成的平面图形的面积的一般步骤 : (1) 作出示意图 ;( 弄清相对位置关系 ) (2) 求交点坐标 ;( 确定积分的上限 , 下限 ) (3) 确定积分变量及被积函数 ; (4) 列式求解 . 定积分在几何中的应用 1. 求下列曲线所围成的图形的面积 : (1)y=x 2 ,y=2x+3; (2)y=e x ,y=e,x=0. 解 : 求两曲线的交点 : 8 2 思考题： 在曲线 y=x 2 (x≥0) 上某点 A 处作切线 , 使之与曲线及 x 轴围成图形的面积为 1/12 。 求过点 A 的切线方程 . A x y o y=x 2 三 . 小结 求两曲线围成的平面图形的面积的一般步骤 : (1) 作出示意图 ;( 弄清相对位置关系 ) (2) 求交点坐标 ;( 确定积分的上限 , 下限 ) (3) 确定积分变量及被积函数 ; (4) 列式求解 . 四 . 作业 :