【推荐】专题07 不等式（第01期）-2016-2017学年高三数学（文）期末优质试卷 19页

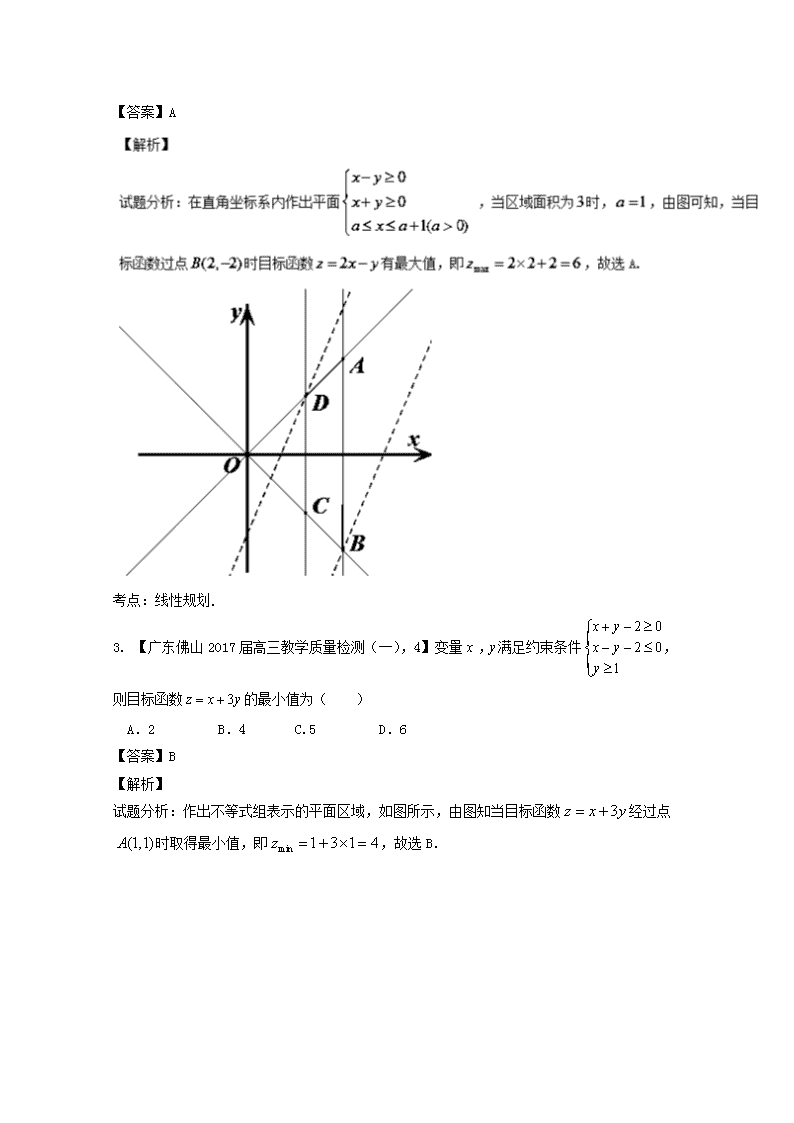
www.ks5u.com 一．基础题组 ‎1. 【河南豫北名校联盟2017届高三上学期精英对抗赛，6】已知实数满足不等式组，若目标函数的最大值不超过4，则实数的取值范围是（ ）‎ A． B． C. D．‎ ‎【答案】D 考点：线性规划.‎ ‎2. 【河北衡水中学2017届高三上学期五调，7】已知为平面区域内的任意一点，当该区域的面积为3时，的最大值是（ ）‎ A．6 B．3 C.2 D．1‎ www.ks5u.com 一．基础题组 ‎1. 【河南豫北名校联盟2017届高三上学期精英对抗赛，6】已知实数满足不等式组，若目标函数的最大值不超过4，则实数的取值范围是（ ）‎ A． B． C. D．‎ ‎【答案】D 考点：线性规划.‎ ‎2. 【河北衡水中学2017届高三上学期五调，7】已知为平面区域内的任意一点，当该区域的面积为3时，的最大值是（ ）‎ A．6 B．3 C.2 D．1‎ ‎【答案】A 考点：线性规划.‎ ‎3. 【广东佛山2017届高三教学质量检测（一），4】变量满足约束条件，则目标函数的最小值为（ ）‎ A．2 B．4 C.5 D．6‎ ‎【答案】B ‎【解析】‎ 试题分析：作出不等式组表示的平面区域，如图所示，由图知当目标函数经过点时取得最小值，即，故选B．‎ 考点：简单的线性规划问题．‎ ‎4. 【广东汕头2017届高三上学期期末，3】若实数满足，则使得取得最大值的最优解为（ ）‎ A． B． C． D．‎ ‎【答案】C 考点：简单的线性规划问题．‎ ‎5. 【山东枣庄2017届高三上学期期末，12】已知实数满足，则的最大值为 ．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：作出不等式组表示的平面区域，如图所示，求的最大值，即求平面区域内任一点与点连线的斜率的最大值，由图可知点与点连线的斜率 最大，即．‎ 考点：简单的线性规划问题．‎ ‎6. 【天津六校2017届高三上学期期中联考，2】设变量满足条件，则目标函数的最小值为(　)‎ ‎ A．2  B．3  C．4  D．5‎ ‎【答案】C ‎7. 【贵州遵义2017届高三上学期期中联考，6】已知，给出下列四个结论：‎ ‎①②③④‎ 其中正确结论的序号是（ ）‎ A．①② B．②③ C．②④ D．③④‎ ‎【答案】C ‎【解析】‎ 试题分析：，因此选C.‎ 考点：不等式性质 ‎8. 【四川2016年普通高考适应性测试，8】实数，满足不等式组，则的最大值为（ ）‎ A． B．0 C.2 D．4‎ ‎【答案】D ‎9. 【广东2017届高三上学期阶段性测评，5】若实数满足，则的最大值为（ ）‎ A． B． C.1 D．2‎ ‎【答案】C ‎【解析】‎ 试题分析：由图可知，当时，取到最大值1.选C.‎ 考点：线性规划 ‎【易错点睛】线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一，准确无误地作出可行域；二，画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三，一般情况下，目标函数的最大或最小值会在可行域的端点或边界上取得.‎ ‎10. 【山西运城2017届高三上学期期中，4】若，，则一定有（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 试题分析：根据，有，由于，两式相乘有，故选B.‎ 考点：不等式的性质.‎ ‎11. 【山西运城2017届高三上学期期中，11】某工厂生产甲、乙两种产品，生产甲产品1件需消耗原料1千克，原料2千克；生产乙产品1件需消耗原料2千克，原料1千克；每件甲产品的利润是300元，每件乙产品的利润是400元，公司在生产这两种产品的计划中，要求每天消耗，原料都不超过12千克，通过合理安排计划，从每天生产的甲，乙两种产品中，公司共可获得的最大利润是（ ）‎ A．1800元 B．2400元 C．2800元 D．3100元 ‎【答案】C 考点：线性规划.‎ ‎【思路点晴】本题主要考查线性规划来解实际应用问题.考查目标函数在线性约束条件下的最大值和最小值问题. 线性目标函数（不全为）中，当时，，这样线性目标函数可看成斜率为，且随变化的一组平行线，则把求的最大值和最小值的问题转化为直线与可行域有公共点，直线在轴上的截距的最大值最小值的问题.因此只需先作出直线，再平行移动这条直线，最先通过或最后通过的可行域的顶点就是最优解.特别注意，当时，的值随着直线在轴上的截距的增大而增大；当时，的值随着直线在轴上的截距的增大而减小.通常情况可以利用可行域边界直线的斜率来判断.‎ ‎12. 【广东湛江市2017届高三上学期期中，15】设满足不等式组，则 的最大值为 ．‎ ‎【答案】‎ ‎13. 【云南大理2017届高三上学期第一次统测，13】设满足约束条件，则的最小值为______________．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：作出不等式组表示的平面区域，如图所示.目标函数表示可行域内的点到原点的距离的平方，显然顶点到原点的距离最大，所以 ‎ 考点：简单的线性规划．‎ ‎14. 【山东潍坊2017届高三上学期期中联考，12】若变量满足约束条件，则目标函数的最小值为 ．‎ ‎【答案】‎ 考点：1、可行域的画法；2、最优解的求法.‎ ‎15. 【贵州遵义2017届高三上学期期中联考，14】已知满足，则目标函数的最大值为___________．‎ ‎【答案】‎ ‎16. 【天津六校2017届高三上学期期中联考，12】设均为正数，且，则的最小值为 .‎ ‎【答案】9‎ ‎17. 【河北唐山2017届高三上期期末，14】设实数满足约束条件，则 ‎ 的最大值等于 ．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：作出不等式组表示的平面区域，如图所示，由图知，当目标函数经过点时取得最大值，所以．‎ 考点：简单的线性规划问题．‎ ‎18. 【四川凉山州2017届高三上学期一诊，14】若，满足不等式则的取值范围是 ．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：在直角坐标系内作出不等式组所表示的可行域如下图所示，由图可知目标函数取得最小值时的最优解为点，即，取得最小值的最优解为点，即，所以的取值范围是.‎ 考点：线性规划.‎ ‎19. 【河南豫北名校联盟2017届高三上学期精英对抗赛，14】已知当时，恒成立，则实数的取值范围是____________.‎ ‎【答案】‎ 考点：函数与不等式恒成立.‎ 二．能力题组 ‎1. 【湖南郴州市2017届高三第二次教学质量监测，9】已知实数，满足不等式组，若目标函数的最大值不超过，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎【答案】D 考点：线性规划.‎ ‎2. 【安徽“皖南八校”2017届高三第二次联考，11】设满足约束条件，则的最小值是（ ）‎ A．9 B．6 C.15 D．‎ ‎【答案】B ‎【解析】‎ 试题分析：可行域为一个三角形ABC及其内部，其中,因此，从而直线过点B时取最小值6，选B.‎ 考点：线性规划 ‎【易错点睛】线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一，准确无误地作出可行域；二，画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三，一般情况下，目标函数的最大或最小值会在可行域的端点或边界上取得.‎ ‎3. 【广西柳州2017届高三上学期10月模拟，10】不等式组（）所表示平面区域的面积为，则的最小值等于（ ）‎ A． B． C． D．‎ ‎【答案】C ‎4. 【中原名校豫南九校2017届上学期第四次质量考评，8】已知实数满足，若目标函数的最小值的7倍与的最大值相等，则实数的值为（ ）‎ A．2 B．1 C. D．‎ ‎【答案】A ‎【解析】‎ 试题分析：过点取最小值5，联立方程，解得，代入 ‎，得.选A.‎ 考点：线性规划 ‎【易错点睛】线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一，准确无误地作出可行域；二，画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三，一般情况下，目标函数的最大或最小值会在可行域的端点或边界上取得.‎ ‎5. 【湖南五市十校教研教改共同体2017届高三上学期12月联考，15】某工厂制作木质的书桌和椅子，需要木工和漆工两道工序，已知木工平均四个小时做一把椅子，八个小时做一张书桌，该工厂每星期木工最多有8000个工作时，漆工平均两小时漆一把椅子，一个小时漆一张书桌，该工厂每星期漆工最多有1300个工作时，又已知制作一把椅子和一张书桌的利润分别是15元和20元，试根据以上条件，生产一个星期能获得的最大利润为___________元．‎ ‎【答案】21000‎ ‎6. 【河北衡水中学2017届高三上学期五调，15】若，则的最小值为 ．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：由得，即，所以 ，，当且仅当 时取等号，所以的最小值为.‎ 考点：1.对数的性质；2.基本不等式.‎ ‎【名师点睛】本题考查对数的性质、基本不等式，属中档题；利用基本不等式求最值时，首先是要注意基本不等式的使用条件，“一正、二定、三相等”；其次在运用基本不等式时，要特别注意适当“拆”、“拼”、“凑”.‎ 三、拔高题组 ‎1. 【天津六校2017届高三上学期期中联考，16】（本题13分）某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大，对某月即将出售的空调和冰箱进行了相关调查，得出下表：‎ 资金 每台空调或冰箱所需资金（百元）‎ 月资金最多供应量（百元）‎ 空调 冰箱 进货成本 ‎30‎ ‎20‎ ‎300‎ 工人工资 ‎5‎ ‎10‎ ‎110‎ 每台利润 ‎6‎ ‎8‎ 问：该商场如果根据调查得来的数据，应该怎样确定空调和冰箱的月供应量，才能使商场获得的总利润最大？总利润的最大值为多少元？‎ ‎【答案】空调和冰箱的月供应量为4台和9台，才能使商场获得的总利润最大，总利润的最大值为9600元 ‎ ‎