2018届二轮复习立体几何中的平行和垂直学案（江苏专用） 6页

热点问题6 立体几何中的平行和垂直 一、填空题 ‎1. 设为两两不重合的平面，m,n,l为两两不重合的直线，给出下列命题： ‎ ‎(1)若；(2)若；‎ ‎(3)若；(4)若 其中真命题是__________ ‎ 答案：(3) (4)‎ ‎2．如图，是平面的斜线段，为斜足．若点在平 面 内运动，使得的面积为定值，则动点的轨迹是__________．‎ ‎(填“圆”“椭圆”“一条直线”“两条平行直线”)‎ 答案：椭圆 解析：考虑到三角形面积为定值，底边一定，从而P到直线AB的距离为定值，若忽略平面的限制，则P轨迹类似为以AB为轴的圆柱面，加上后者平面，轨迹为圆柱面与平面的交集，轨迹为椭圆。‎ ‎3．棱长为a的正四面体(侧棱长等于底面边长的正三棱锥)ABCD的四个顶点均在同一个球面上，则此球的半径R＝________．‎ 答案：a 解析：相关组合体的转化和计算，借助球内接正方体 ‎4．如图，已知三棱锥A—BCD的底面是等边三角形，三条侧棱长都等于1，且∠BAC＝30°，M、N分别在棱AC和AD上，则 BM＋MN＋NB的最小值为 ．‎ 答案： ‎ 解析：多面体(旋转体)表面上两点间的最短路径与展开图将三棱锥A—BCD的侧面沿AB“展开”在同一平面上．‎ ‎5．正三棱锥中，，，分别是棱上的点，为边的中点，，则三角形的面积为 ．‎ 答案：‎ 解析：由为边的中点得，又得且交于点，另由，可求得为 的中点，从而，则的面积为。‎ ‎6．已知三棱锥的所有顶点都在球的球面上，是边长为的正三角形，为球的直径，且；则此棱锥的体积为 ．‎ 答案：‎ 解析： 的外接圆的半径，点到面的距离,为球的直径点到面的距离为， 此棱锥的体积为．‎ ‎7．设m、n是异面直线，则 ‎(1)一定存在平面，使m⊂且n∥； ‎ ‎(2)一定存在平面，使m⊂且n⊥；‎ ‎(3)一定存在平面γ，使m、n到γ的距离相等；‎ ‎(4)一定存在无数对平面与，使m⊂，n⊂，且∥. ‎ 上述4个命题中正确命题的序号为________．‎ 答案：（1）（3）‎ ‎8．已知正四棱锥中，，那么当该棱锥的体积取最大时，高为 . 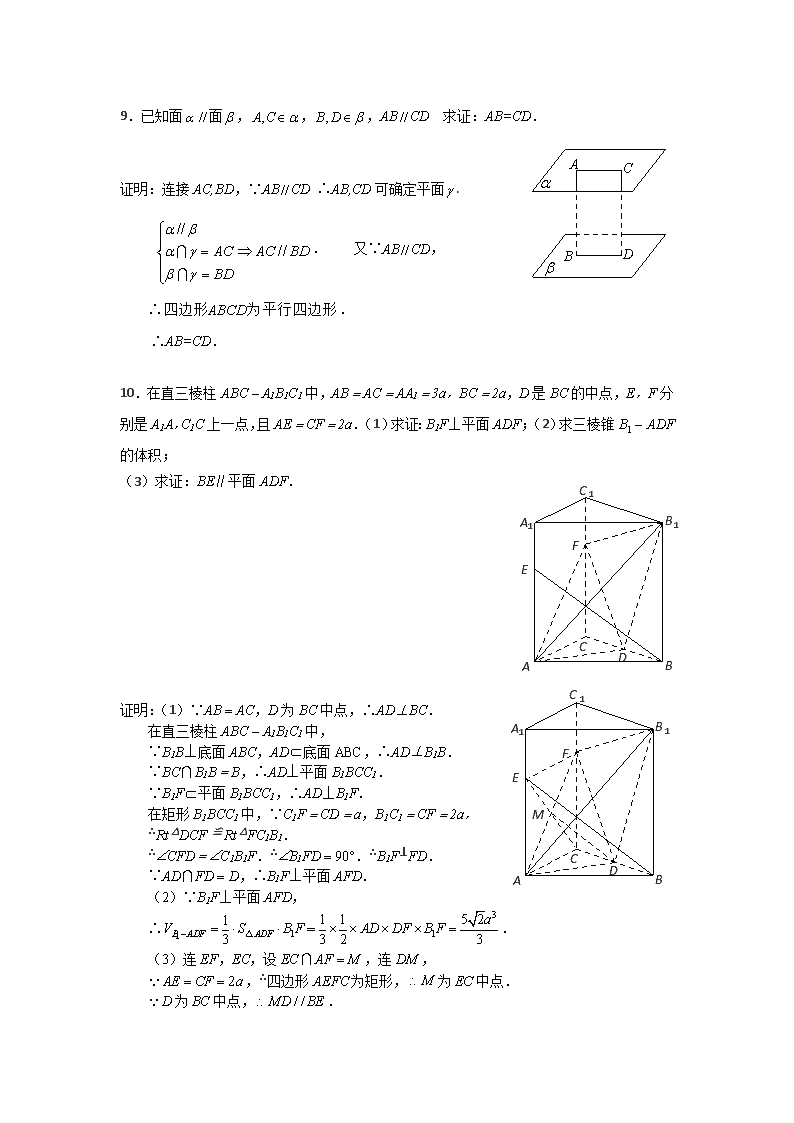‎ 答案：2‎ 解析：考察锥体的体积，考察函数的最值问题.设底面边长为a，则高所以，设，则，当y取最值时，，解得或时，体积最 大，此时 二、解答题 ‎9．已知面面，，，ABCD 求证：AB=D C B A CD．‎ 证明：连接AC,BD，∵ABCD ∴AB,CD可确定平面.‎ ‎． 又∵ABCD，‎ ‎∴． ‎ ‎∴AB=CD．‎ ‎10．在直三棱柱ABC - A1B1C1中，AB = AC = AA1 = 3a，BC = 2a，D是BC的中点，E，F分别是A1A，C1C上一点，且AE = CF = 2a．（1）求证：B1F⊥平面ADF；（2）求三棱锥B1 - ADF的体积；‎ A ‎ F ‎ C ‎ B ‎ D ‎ C ‎ B ‎ ‎1 ‎ ‎1 ‎ ‎1 ‎ E ‎ ‎1 ‎ ‎1 ‎ ‎1 ‎ A ‎ ‎（3）求证：BE∥平面ADF．‎ A ‎ F ‎ C ‎ B ‎ D ‎ C ‎ B ‎ ‎1 ‎ ‎1 ‎ ‎1 ‎ E ‎ ‎1 ‎ ‎1 ‎ ‎1 ‎ A ‎ M ‎ ‎ ‎ 证明：（1）∵AB = AC，D为BC中点，∴AD⊥BC． ‎ 在直三棱柱ABC - A1B1C1中，‎ ‎∵B1B⊥底面ABC，AD底面ABC，∴AD⊥B1B． ‎ ‎∵BCB1B = B，∴AD⊥平面B1BCC1．‎ ‎∵B1F平面B1BCC1，∴AD⊥B1F． ‎ 在矩形B1BCC1中，∵C1F = CD = a，B1C1 = CF = 2a，‎ ‎∴Rt△DCF ≌ Rt△FC1B1．‎ ‎∴ÐCFD = ÐC1B1F．∴ÐB1FD = 90°．∴B1F⊥FD．‎ ‎∵ADFD = D，∴B1F⊥平面AFD． ‎ ‎（2）∵B1F⊥平面AFD，‎ ‎∴=．‎ ‎（3）连EF，EC，设，连，‎ ‎，∴四边形AEFC为矩形，为中点．‎ 为中点，． ‎ 平面，．平面，平面 ‎ ‎11．如图，平面PAC平面ABC，ACBC,PECB,M是AE的中点.‎ ‎(1)若N是PA的中点，求证：平面CMN平面PAC;‎ ‎(2)若MN平面ABC，求证：N是PA的中点.‎ N M E P C B A 证明（1）∵平面PAC平面ABC, 平面PAC平面ABC=AC, ACBC, ‎ 平面ABC ∴BC平面PAC ‎∵M是AE的中点, N是PA的中点 ∴MNPE 又∵PEBC ∴MNBC ∴MN平面PAC ‎ 又∵MN平面CMN ∴平面CMN平面PAC ‎(2)设平面PAE平面ABC=l 又∵MN平面ABC, MN平面PAE ∴MNl ‎∵PEBC, PE平面ABC,BC平面ABC ∴PE平面ABC ‎∵PE平面PAE, 平面PAE平面ABC=l ∴PEl ∴PEMN ‎∵M是AE的中点 ∴N是PA的中点.‎ ‎12．如图，在直三棱柱ABCA1B1C1中，ACBC，CC1= 4，是棱CC1上的一点．‎ ‎（1）求证：BCAM ； ‎ ‎（2）若N是AB的中点，且CN∥平面，求CM的长．‎ C ‎【解】（1）因为是直三棱柱，所以平面，‎ 因为平面，所以． ‎ 因为，，平面，所以平面．‎ C 图1‎ 因为平面，所以． ‎ ‎（2）证法一：如图1，取的中点，连结，．‎ 因为是的中点，所以， ‎ 因为，所以，所以与共面． ‎ 因为∥平面，平面平面，所以． ‎ C 图2‎ 所以四边形为平行四边形，所以 证法二：如图2，设与确定的平面交于点，‎ 连结，．‎ 因为∥平面，平面，‎ 平面平面，所以． ‎ 因为，平面，平面，所以平面． ‎ 又平面，平面平面，所以，‎ Q C 图3‎ 所以，所以四边形为平行四边形．因为是的中点，‎ 所以． ‎ 证法三：如图3，取的中点，‎ 连结，．‎ 因为是的中点，所以，‎ 因为平面，平面，所以平面． ‎ 因为CN∥平面，，平面，‎ 所以平面平面． ‎ 因为平面平面，平面平面，‎ 所以． ‎ 因为，所以四边形是平行四边形，‎ 所以． ‎ 证法四：如图4，分别延长，设交点为S，连结AC．‎ C 图4‎ 因为∥平面，平面，‎ 平面平面，‎ 所以∥AS．由于AN=NB，所以BC=CS．‎ 又因为∥，同理可得，， ‎ 所以． ‎