数学文卷·2018届湖北省孝感市八所重点高中教学协作体高二7月联合考试（2017-07） 9页

孝感市八所重点高中教学协作体2016—2017学年联合考试 高二文科数学试卷 命题学校：云梦一中 ‎ 考试时间：‎2017年7月1日上午10:00——12:00 试卷满分：150分 一、选择题：本大题共12个小题,每小题5分,在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.复数的共轭复数是 （ ）‎ ‎ A. B. C. D. ‎ ‎2. 下列说法中错误的是 （ ）‎ ‎ A. 若命题，则 ‎ B.“”是“”的充分不必要条件 ‎ C. 命题“若”的逆否命题为:“若，则‎0”‎ ‎ D. 若为假命题，则均为假命题 ‎3. 若集合，B={x|x2﹣5x+6=0}，则A∩B=（　　）‎ A．[2，3] B． C．2 D．{2，3}‎ ‎4. 若 则 A． B． C． D．‎ ‎5. 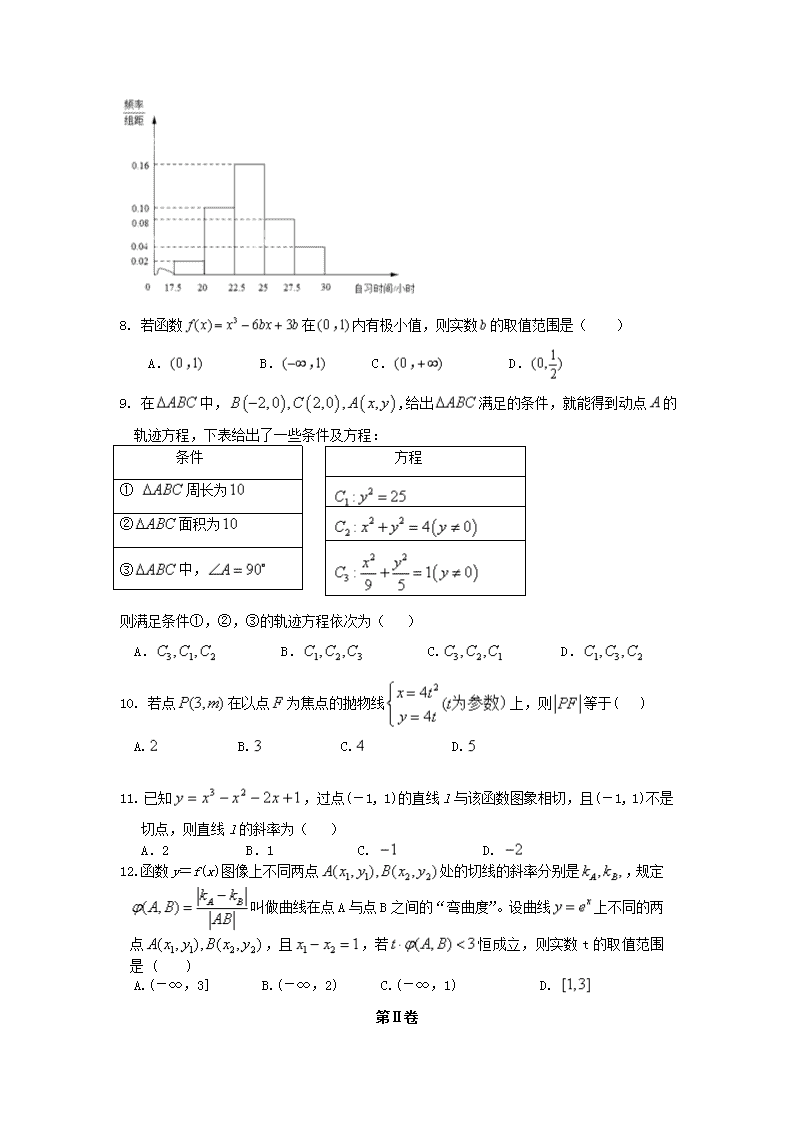已知a1＝3，a2＝6，且an＋2＝an＋1－an，则a2017＝( 　)‎ ‎ A． 3 B．－3 C．6 D．－6‎ ‎6. 某高校调查了200名学生每周的自习时间（单位：小时），制成了如下图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20)， [20，22.5)， [22.5,25)，[25，27.5)，[27.5，30).根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是（ ）‎ A. 56 B. ‎60 ‎ C. 120 D. 140‎ ‎7. 阅读如下图的程序框图. 若输入, 则输出的值为（ ）‎ ‎ A. B. C. D.‎ ‎8. 若函数在内有极小值，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎9. 在中，,给出满足的条件，就能得到动点的轨迹方程，下表给出了一些条件及方程：‎ 条件 ‎① 周长为 ‎②面积为 ‎③中，‎ 方程 则满足条件①，②，③的轨迹方程依次为（ ）‎ ‎ A． B． C. D．‎ ‎10. 若点在以点为焦点的抛物线上，则等于( )‎ ‎ A. B. C. D.‎ ‎11. 已知，过点(－1, 1)的直线l与该函数图象相切，且(－1, 1)不是切点，则直线l的斜率为（ ） ‎ A．2 B．1 C. D. ‎ ‎12. 函数y＝f(x)图像上不同两点处的切线的斜率分别是，规定叫做曲线在点A与点B之间的“弯曲度”。设曲线上不同的两点，且，若恒成立，则实数t的取值范围是 ( )‎ A.(－∞，3] B.(－∞，2) C.(－∞，1) D. ‎ 第Ⅱ卷 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 从这四个数中随机取出两个数组成一个两位数,则组成的两位数是的倍数的概率是_______ _．‎ ‎14. 观察下列等式： ‎ ‎ 1＝1‎ ‎ 2＋3＋4＝9‎ ‎ 3＋4＋5＋6＋7＝25‎ ‎ 4＋5＋6＋7＋8＋9＋10＝49‎ ‎ ……‎ ‎ 照此规律，第n个等式为_______ _．‎ ‎15. 不等式的解集为 。‎ ‎16. 函数与的图象上存在关于轴对称的点， ‎ ‎ 则实数的取值范围是 。‎ 三、解答题 （解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17．（本小题满分10分）‎ 已知直线l的极坐标方程为2ρsin＝，点A的极坐标为A，‎ 曲线C的参数方程为(t为参数)．‎ ‎ （1）求点A到直线l的距离;‎ ‎ （2）设直线l与曲线C相交与P, Q两点，求P, Q两点之间的距离。‎ ‎18．（本小题满分12分）‎ 已知函数f(x)＝|2x－1|＋|x－‎2a|.‎ ‎（1）当a＝1时，求f(x)≤3的解集；‎ ‎（2）当x∈[1,2]时，f(x)≤3恒成立，求实数a的取值范围。‎ ‎19. （本小题满分12分）‎ 已知函数 ‎ （1）求的单调区间；‎ ‎ （2）若在[0，1]上单调递增，求a的取值范围。‎ ‎20. （本小题满分12分）‎ ‎ 全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续天监测空气质量指数，数据统计如下：‎ 空气质量指数 空气质量等级 空气优 空气良 轻度污染 中度污染 重度污染 天数 ‎ （1）根据所给统计表和频率分布直方图中的信息求出的值，并完成頻率分布直方图：‎ ‎ （2）由頻率分布直方图，求该组数据的平均数与中位数；‎ ‎ （3）在空气质量指数分别为和的监测数据中，用分层抽样的方法抽取 ‎ 天，从中任意选取天，求事件“两天空气都为良”发生的概率.‎ ‎21. （本小题满分12分）‎ ‎ 已知，函数的最小值为2．‎ ‎ （1）求的值；‎ ‎ （2）证明：与不可能同时成立．‎ ‎22. （本小题满分12分）‎ 已知函数的图像C在点处切线的斜率为，函数 为奇函数，且其图像为.‎ (1) 求实数的值;‎ ‎(2) 当时，图像C恒在的上方，求实数的取值范围;‎ ‎(3) 若图像C与有两个不同的交点A，B，其横坐标分别是设 ‎ 求证：‎ 高二数学（文科）参考答案 一、选择题（本大题共12小题，每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D D B A D B D A C C ‎ A 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13. 14. ‎ ‎15. 16. ‎ 三、解答题：本大题共6小题，共70分.‎ ‎17．解：(1)由2ρsin＝，‎ 得2ρ＝，所以y－x＝1，‎ 故直线l的直角坐标方程为x－y＋1＝0，‎ 而点A对应的直角坐标为A(2，－2)，‎ 所以点A(2，－2)到直线l：x－y＋1＝0的距离为＝ …………5分 ‎(2)曲线C的直角坐标方程是：x2＋y2＝2，圆心到直线距离 所以弦长PQ= …………………10分 ‎18. 解：(1)当a＝1时，由f(x)≤3，可得|2x－1|＋|x－2|≤3，‎ ‎∴①或②‎ 或③‎ 解①求得0≤x＜；解②求得≤x＜2；解③求得x＝2.‎ 综上可得，0≤x≤2，即不等式的解集为[0,2]．……………………6分 ‎(2)∵当x∈[1,2]时，f(x)≤3恒成立，‎ 即|x－‎2a|≤3－|2x－1|＝4－2x，‎ 故2x－4≤‎2a－x≤4－2x，即3x－4≤‎2a≤4－x.‎ 再根据3x－4的最大值为6－4＝2，‎ ‎4－x的最小值为4－2＝2，‎ ‎∴‎2a＝2，∴a＝1，‎ 即a的取值范围为{1}……………………12分 ‎19解：（I）‎ ‎ 1、‎ ‎ 当且仅当时取“=”号，单调递增。 ……………3分 ‎ 2、‎ ‎ 单调增区间：‎ ‎ 单调减区间： ……………6分 ‎（II）当 则是上述增区间的子集：‎ ‎1、时，单调递增 符合题意 ‎2、， ‎ 综上，a的取值范围是[0，1]。 ……………12分 ‎20. 解：(1),‎ ‎. ‎ ‎………4分 ‎(2)平均数 ，中位数. ………8分 ‎(3) 在空气质量指数为和的监测天数中分别抽取天和天，在所抽収的天中，将空气质量指数为的天分别记为；将空气质量指数为的天记为，从中任取天的基本事件分别为：共种，其中 事件“两天空气都为良”包含的基本事件为共种，所以事件“两天都为良”发生的概率是. ………12分 ‎21. 解：（1）∵，‎ ‎∴，‎ ‎∴．‎ 由题设条件知， ‎ ‎∴． ……………6分 ‎（2）由（1）及基本不等式，得，∴． ‎ 假设与同时成立，则由及，得．‎ 同理，∴，这与矛盾．‎ 故与不可能同时成立． ………12分 ‎22. 解：.（1） 2分 为奇函数， 3分