高一数学（人教A版）必修2能力强化提升：2-3-2 平面与平面垂直的判定 12页

一、选择题 ‎1．下列命题中：①两个相交平面组成的图形叫做二面角；②异面直线a，b分别和一个二面角的两个面垂直，则a，b所成的角与这个二面角相等或互补；③二面角的平面角是从棱上一点出发，分别在两个面内作射线所成角的最小角；④二面角的大小与其平面角的顶点在棱上的位置没有关系，其中正确的是(　　)‎ A．①③ B．②④‎ C．③④ D．①②‎ ‎[答案]　B ‎[解析]　对①，显然混淆了平面与半平面的概念，是错误的；对②，由于a，b分别垂直于两个面，所以也垂直于二面角的棱，但由于异面直线所成的角为锐角(或直角)，所以应是相等或互补，是正确的；对③，因为不垂直于棱，所以是错误的；④是正确的，故选B.‎ ‎[点评]　根据二面角的相关概念进行分析判定．‎ ‎2．以下三个命题中，正确的命题有(　　)‎ ‎①一个二面角的平面角只有一个；②二面角的棱垂直于这个二面角的平面角所在的平面；③分别在二面角的两个半平面内，且垂直于棱的两直线所成的角等于二面角的大小 A．0个 B．1个 C．2个 D．3个 ‎[答案]　B ‎[解析]　仅②正确．‎ ‎3．正方体ABCD－A1B‎1C1D1的六个面中，与平面BC1垂直的面的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ ‎[答案]　D ‎[解析]　与平面BC1垂直的面有：平面AC，平面A‎1C1，平面AB1，平面CD1.‎ ‎4．自二面角内任意一点分别向两个面引垂线，则两垂线的夹角与二面角的平面角的关系是(　　)‎ A．相等 B．互补 C．互余 D．无法确定 ‎[答案]　B ‎[解析]　如图，BD、CD为AB、AC所在平面与α、β的交线，则∠BDC为二面角α－l－β的平面角．且∠ABD＝∠ACD＝90°，∴∠A＋∠BDC＝180°.‎ ‎5．已知α，β是平面，m、n是直线，给出下列表述：‎ ‎①若m⊥α，m⊂β，则α⊥β；‎ ‎②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；‎ ‎③如果m⊂α，n⊄α，m，n是异面直线，那么n与α相交；‎ ‎④若α∩β＝m，n∥m，且n⊄α，n⊄β，则n∥α且n∥β.‎ 其中表述正确的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ ‎[答案]　B ‎[解析]　①是平面与平面垂直的判定定理，所以①正确；②中，m，n不一定是相交直线，不符合两个平面平行的判定定理，所以②不正确；③中，还可能n∥α，所以③不正确；④中，由于n∥m，n⊄α，m⊂α，则n∥α，同理n∥β，所以④正确．‎ ‎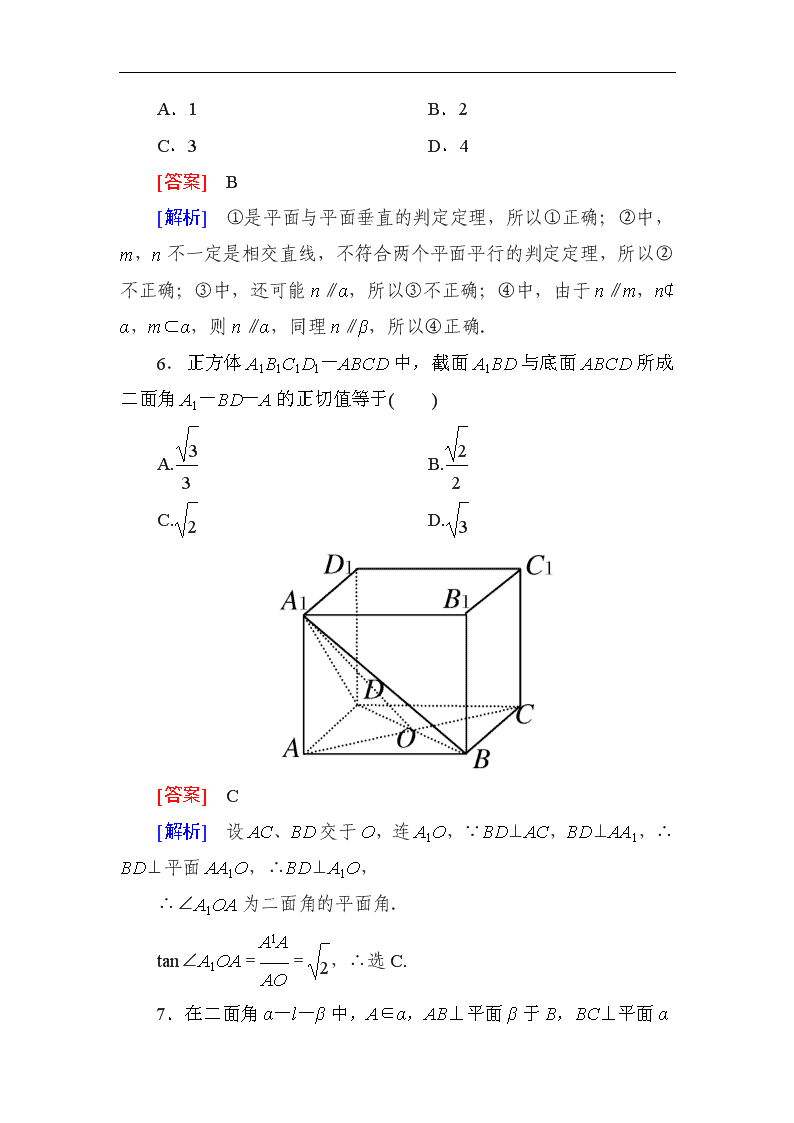6．正方体A1B‎1C1D1－ABCD中，截面A1BD与底面ABCD所成二面角A1－BD－A的正切值等于(　　)‎ A. B. C. D. ‎[答案]　C ‎[解析]　设AC、BD交于O，连A1O，∵BD⊥AC，BD⊥AA1，∴BD⊥平面AA1O，∴BD⊥A1O，‎ ‎∴∠A1OA为二面角的平面角．‎ tan∠A1OA＝＝，∴选C.‎ ‎7．在二面角α－l－β中，A∈α，AB⊥平面β于B，BC⊥平面α于C，若AB＝6，BC＝3，则二面角α－l－β的平面角的大小为(　　)‎ A．30° B．60°‎ C．30°或150° D．60°或120°‎ ‎[答案]　D ‎[解析]　如图，∵AB⊥β，∴AB⊥l，∵BC⊥α，∴BC⊥l，∴l⊥平面ABC，‎ 设平面ABC∩l＝D，‎ 则∠ADB为二面角α－l－β的平面角或补角，‎ ‎∵AB＝6，BC＝3，‎ ‎∴∠BAC＝30°，∴∠ADB＝60°，‎ ‎∴二面角大小为60°或120°.‎ ‎8．四边形ABCD是正方形，以BD为棱把它折成直二面角A－BD－C，E为CD的中点，则∠AED的大小为(　　)‎ A．45° B．30°‎ C．60° D．90°‎ ‎[答案]　D ‎[解析]　设BD中点为F，则AF⊥BD，CF⊥BD，‎ ‎∴∠AFC＝90°，∴AF⊥面BCD.‎ ‎∵E、F分别为CD、BD的中点，‎ ‎∴EF∥BC，‎ ‎∵BC⊥CD，∴CD⊥EF，‎ 又AF⊥CD，∴CD⊥平面AEF，∴CD⊥AE.故选D.‎ 二、填空题 ‎9．下列四个命题中，正确的命题为________(填序号)．‎ ‎①α∥β，β⊥γ，则α⊥γ ‎②α∥β，β∥γ，则α∥γ ‎③α⊥β，γ⊥β，则α⊥γ ‎④α⊥β，γ⊥β，则α∥γ ‎[答案]　①②‎ ‎10．在三棱锥P－ABC中，已知PA⊥PB，PB⊥PC，PC⊥PA ‎，如右图所示，则在三棱锥P－ABC的四个面中，互相垂直的面有________对．‎ ‎[答案]　3‎ ‎[解析]　∵PA⊥PB，PA⊥PC，PB∩PC＝P，‎ ‎∴PA⊥平面PBC，‎ ‎∵PA⊂平面PAB，PA⊂平面PAC，‎ ‎∴平面PAB⊥平面PBC，平面PAC⊥平面PBC.同理可证：平面PAB⊥平面PAC.‎ ‎11．如图所示，在长方体ABCD－A1B‎1C1D1中，BC＝2，AA1＝1，E，F分别在AD和BC上，且EF∥AB，若二面角C1－EF－C等于45°，则BF＝________.‎ ‎[答案]　1‎ ‎[解析]　∵AB⊥平面BC1，C‎1F⊂平面BC1，CF⊂平面BC1，∴AB⊥C‎1F，AB⊥CF，又EF∥AB，‎ ‎∴C‎1F⊥EF，CF⊥EF，‎ ‎∴∠C1FC是二面角C1－EF－C的平面角，‎ ‎∴∠C1FC＝45°，‎ ‎∴△FCC1是等腰直角三角形，‎ ‎∴CF＝CC1＝AA1＝1.‎ 又BC＝2，∴BF＝BC－CF＝2－1＝1.‎ ‎12．如图，四边形ABCD是正方形，PA⊥平面ABCD，且PA＝AB＝a.‎ ‎(1)二面角A－PD－C的度数为________；‎ ‎(2)二面角B－PA－D的度数为________；‎ ‎(3)二面角B－PA－C的度数为________；‎ ‎(4)二面角B－PC－D的度数为________．‎ ‎[答案]　90°；90°；45°；120°‎ ‎[解析]　(1)PA⊥平面ABCD，∴PA⊥CD.‎ 又四边形ABCD为正方形，∴CD⊥AD，∴CD⊥平面PAD，‎ 又CD⊂平面PCD，∴平面PAD⊥平面PCD，‎ ‎∴二面角A－PD－C为90°.‎ ‎(2)∵PA⊥平面ABCD，∴AB⊥PA，AD⊥PA，‎ ‎∴∠BAD为二面角B－AP－D的平面角．‎ 又∠BAD＝90°，∴二面角B－AP－D为90°.‎ ‎(3)PA⊥平面ABCD，∴AB⊥PA，AC⊥PA，‎ ‎∴∠BAC为二面角B－PA－C的平面角，‎ 又四边形ABCD为正方形，∴∠BAC＝45°，‎ 即二面角B－PA－C为45°.‎ ‎(4)作BE⊥PC于E，连DE，‎ 则由△PBC≌△PDC知∠BPE＝∠DPE，‎ 从而△PBE≌△PDE，‎ ‎∴∠DEP＝∠BEP＝90°，且BE＝DE，‎ ‎∴∠BED为二面角B－PC－D的平面角．‎ ‎∵PA⊥平面ABCD，∴PA⊥BC，又AB⊥BC，‎ ‎∴BC⊥平面PAB，∴BC⊥PB，‎ ‎∴BE＝＝a，BD＝a，‎ ‎∴取BD中点O，则sin∠BEO＝＝，‎ ‎∴∠BEO＝60°，∴∠BED＝120°‎ ‎∴二面角B－PC－D的度数为120°.‎ 三、解答题 ‎13．(2012·江西卷)如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB＝12，AD＝5，BC＝4，DE＝4.现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG.‎ ‎(1)求证：平面DEG⊥平面CFG；‎ ‎(2)求多面体CDEFG的体积．‎ ‎[解析]　(1)由已知可得AE＝3，BF＝4，则折叠完后EG＝3，GF＝4，又因为EF＝5，所以可得EG⊥GF，又因为CF⊥底面EGF，可得CF⊥EG，即EG⊥面CFG所以平面DEG⊥平面CFG.‎ ‎(2)过G作GO垂直于EF，GO即为四棱锥G－EFCD的高，所以所求体积为S矩DECF·GO＝×5×4×＝16.‎ ‎14．在如下图所示的四面体ABCD中，AB，BC，CD两两互相垂直，且BC＝CD.‎ ‎(1)求证：平面ACD⊥平面ABC；‎ ‎(2)求二面角C－AB－D的大小．‎ ‎[分析]　(1)转化为证明CD⊥平面ABC；‎ ‎(2)∠CBD是二面角C－AB－D的平面角．‎ ‎[解析]　(1)证明：∵CD⊥AB，CD⊥BC，AB∩BC＝B，‎ ‎∴CD⊥平面ABC.‎ 又∵CD⊂平面ACD，∴平面ACD⊥平面ABC.‎ ‎(2)∵AB⊥BC，AB⊥CD，且BC∩CD＝C，‎ ‎∴AB⊥平面BCD.∴AB⊥BD.‎ ‎∴∠CBD是二面角C－AB－D的平面角．‎ ‎∵在Rt△BCD中，BC＝CD，∴∠CBD＝45°.‎ ‎∴二面角C－AB－D的大小为45°.‎ ‎15．已知PA⊥平面ABCD，四边形ABCD为矩形，PA＝AD，M、N分别是AB、PC的中点，求证：‎ ‎(1)MN∥平面PAD；‎ ‎(2)平面PMC⊥平面PDC.‎ ‎[解析]　(1)取PD的中点Q，连接AQ、QN，‎ ‎∵PN＝NC，∴QN綊DC.‎ ‎∵四边形ABCD为矩形，‎ ‎∴QN綊AM，‎ ‎∴MN∥AQ，‎ 又∵AQ⊂平面PAD，MN⊄平面PAD，‎ ‎∴MN∥平面PAD.‎ ‎(2)∵PA⊥平面ABCD，∴∠PAD＝90°，‎ ‎∴△PAD为等腰直角三角形，‎ ‎∵Q为PD中点，∴AQ⊥PD，‎ ‎∵CD⊥AD，CD⊥PA，∴CD⊥平面PAD，‎ ‎∵AQ⊂平面PAD，∴CD⊥AQ，∴AQ⊥平面PDC 由(1)MN∥AQ，∴MN⊥平面PDC，‎ 又∵MN⊂平面PMC，∴平面PMC⊥平面PDC.‎ ‎16．如图所示，四棱锥P－ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝.‎ ‎(1)证明：平面PBE⊥平面PAB；‎ ‎(2)求二面角A－BE－P的大小．‎ ‎[解析]　(1)证明：如图所示，连接BD，由ABCD是菱形且∠BCD＝60°知，△BCD是等边三角形．‎ 因为E是CD的中点，所以BE⊥CD，‎ 又AB∥CD，所以BE⊥AB，‎ 又因为PA⊥平面ABCD，BE⊂平面ABCD，所以PA⊥BE.‎ 而PA∩AB＝A，因此BE⊥平面PAB.‎ 又BE⊂平面PBE，所以平面PBE⊥平面PAB.‎ ‎(2)由(1)知，BE⊥平面PAB，PB⊂平面PAB，所以PB⊥BE.又AB⊥BE，所以∠PBA是二面角A－BE－P的平面角．‎ 在Rt△PAB中，tan∠PBA＝＝，∠PBA＝60°.‎ 故二面角A－BE－P的大小是60°.‎