广东广州市天河区普通高中2018届高考数学一轮复习精选试题：推理与证明（选择与填空） 6页

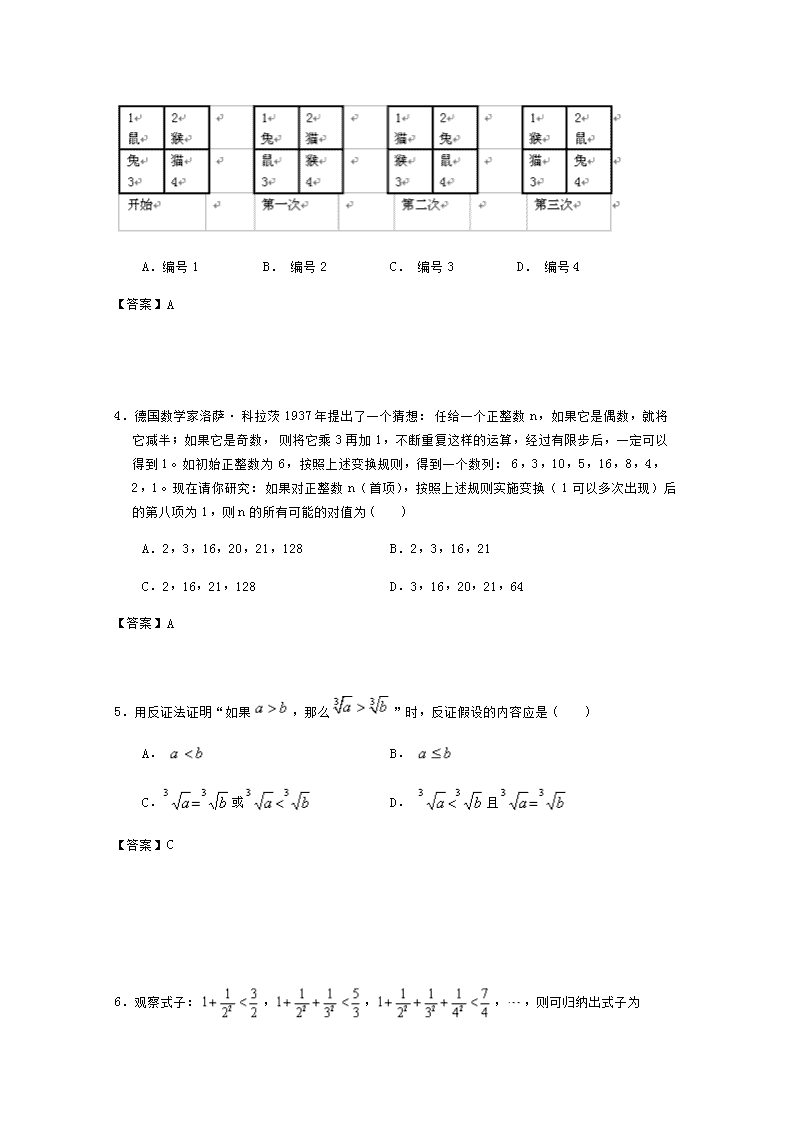
全*品*高*考*网， 用后离不了！推理与证明01‎ 一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是( )‎ A．假设三内角都不大于60度 B．假设三内角都大于60度 C．假设三内角至多有一个大于60度 D．假设三内角至多有两个大于60度 ‎【答案】B ‎2．下列不等式不成立的是( )‎ A． a2+b2+c2ab+bc+ca B． (a>0,b>0)‎ C． (a3)‎ D． <‎ ‎【答案】D ‎3．四个小动物换座位，开始是鼠、猴、兔、猫分别坐1，2，3，4号位子上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…，这样交替进行下去，那么第2009次互换座位后，小兔的座位对应的是( )‎ A．编号1 B． 编号2 C． 编号3 D． 编号4‎ ‎【答案】A ‎4．德国数学家洛萨·科拉茨1937年提出了一个猜想：任给一个正整数n，如果它是偶数，就将它减半；如果它是奇数，则将它乘3再加1，不断重复这样的运算，经过有限步后，一定可以得到1。如初始正整数为6，按照上述变换规则，得到一个数列：6，3，10，5，16，8，4，2，1。现在请你研究：如果对正整数n（首项），按照上述规则实施变换（1可以多次出现）后的第八项为1，则n的所有可能的对值为( )‎ A．2，3，16，20，21，128 B．2，3，16，21‎ C．2，16，21，128 D．3，16，20，21，64‎ ‎【答案】A ‎5．用反证法证明“如果，那么”时，反证假设的内容应是( )‎ A． B． ‎ C．或 D． 且 ‎【答案】C ‎6．观察式子：，，，‎ ‎，则可归纳出式子为( )‎ A． B．‎ C． D．‎ ‎【答案】C ‎7．用反证法证明“如果a>b，那么”假设的内容应是( )‎ A． B． ‎ C．且 D．或 ‎【答案】D ‎8．已知数列{an}的前n项和Sn＝n2an(n≥2)，而a1＝1，通过计算a2，a3，a4，猜想an等于( )‎ A． B． C． D． ‎【答案】B ‎9．用反证法证明命题：“若整数系数一元二次方程有有理根，那么 中至少有一个是偶数”时，应假设( )‎ A．中至多一个是偶数 B． 中至少一个是奇数 ‎ C． 中全是奇数 D． 中恰有一个偶数 ‎【答案】C ‎10．用反证法证明命题“三角形的内角中至少有一个不大于”时，反设正确的是( )‎ A．假设三内角都大于 B．假设三内角都不大于 ‎ C．假设三内角至多有一个大于 D．假设三内角至多有两个大于 ‎【答案】A ‎11．用反证法证明“方程至多有两个解”的假设中，正确的是( )‎ A． 至多有一个解 B． 有且只有两个解 C． 至少有三个解 D． 至少有两个解 ‎【答案】C ‎12．用反证法证明命题：“,,,且,则中至少有一个负数”时的假设为( )‎ A．中至少有一个正数 B．全为正数 C．中至多有一个负数 D．全都大于等于0‎ ‎【答案】D 二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)‎ ‎13．2011年11月2日，即20111102，正好前后对称，因而被称为“完美对称日”，请你写出本世纪的一个 “完美对称日”： 　　　 ．‎ ‎【答案】如：20011002,20100102等 ‎14．在如图所示的数表中，第行第列的数记为，且满足， ，记第3行的数3，5，8，13，22， 依次组成数列，则数列的通项公式为 。 ‎ ‎【答案】‎ ‎15．研究问题：“已知关于的不等式的解集为，解关于的不等式”，有如下解法：‎ 解：由，令，则，‎ 所以不等式的解集为．‎ ‎ 参考上述解法，已知关于的不等式的解集为，则关于的不等式的解集为 ‎ ‎【答案】‎ ‎16．有下列各式：，，…，则按此规律可猜想此类不等式的一般形式为 (n∈N*)．‎ ‎【答案】1＋＋＋…＋>(n∈N*)‎