2021届课标版高考理科数学大一轮复习课件：8-3　直线、平面平行的判定与性质（讲解部分） 30页

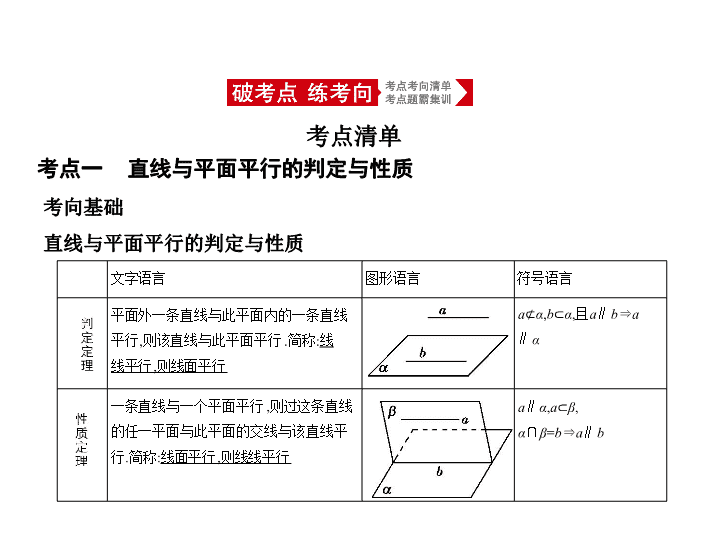
8.3 　直线、平面平行的判定与性质 高考理数 考点一    直线与平面平行的判定与性质 考点清单 考向基础 直线与平面平行的判定与性质 文字语言 图形语言 符号语言   平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简称: 线线平行,则线面平行   a ⊄ α , b ⊂ α ,且 a ∥ b ⇒ a ∥ α   一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.简称: 线面平行,则线线平行   a ∥ α , a ⊂ β , α ∩ β = b ⇒ a ∥ b 内,且 a ∥ b ,否则会出现错误.(2)一条直线平行于一个平面,它可以与平面内 的无数条直线平行,但这条直线与平面内的任意一条直线可能平行,也可能 异面.(3) a ∥ α 的判定定理和性质定理使用的区别:如果结论中有 a ∥ α ,则要 用判定定理,在 α 内找与 a 平行的直线;若条件中有 a ∥ α ,则要用性质定理,找 (或作)过 a 且与 α 相交的平面. 注意　(1)在推证线面平行时,一定要强调直线 a 不在平面内,直线 b 在平面 考向突破 考向一    证明直线与平面平行 例1     (2019新疆乌鲁木齐二模,18)如图,在直三棱柱 A 1 B 1 C 1 - ABC 中, AB ⊥ AC , AB = AC =2, AA 1 =4,点 D 是 BC 的中点. (1)证明:直线 A 1 B ∥平面 AC 1 D ; (2)求点 A 1 到平面 AC 1 D 的距离.   解析 　(1)证明:连接 A 1 C 交 AC 1 于 E ,连接 DE ,则 E 是 A 1 C 的中点, 又 D 是 BC 的中点, ∴ DE ∥ A 1 B , 又 A 1 B ⊄ 平面 AC 1 D , DE ⊂ 平面 AC 1 D , ∴ A 1 B ∥平面 AC 1 D . (2)∵ AB = AC =2, AA 1 =4, AB ⊥ AC , ∴ AD = CD =   , AC 1 =   =2   , DC 1 =   =3   , ∴   =     · AB =   ×   × 2 × 4 × 2=   , ∵ D 是 BC 的中点, ∴   =     =   . ∵ AD 2 + D   = A   , ∴ AD ⊥ DC 1 , ∴   =   ×   × 3   =3. 设 A 1 到平面 AC 1 D 的距离为 h , 则   =   × 3 × h = h , 又   =   ,∴ h =   . ∴ A 1 到平面 AC 1 D 的距离为   . 考向二    证明直线与直线平行 例2 　如图,在多面体 ABCDEF 中, DE ⊥平面 ABCD , AD ∥ BC ,平面 BCEF ∩ 平 面 ADEF = EF ,∠ BAD =60 ° , AB =2, DE = EF =1.   (1)求证: BC ∥ EF ; (2)求三棱锥 B - DEF 的体积. 解析 　(1)证明:∵ AD ∥ BC , AD ⊂ 平面 ADEF , BC ⊄ 平面 ADEF ,∴ BC ∥平面 ADEF .又 BC ⊂ 平面 BCEF ,平面 BCEF ∩ 平面 ADEF = EF ,∴ BC ∥ EF . (2)过点 B 作 BH ⊥ AD 于点 H .   ∵ DE ⊥平面 ABCD , BH ⊂ 平面 ABCD , ∴ DE ⊥ BH . ∵ AD ⊂ 平面 ADEF , DE ⊂ 平面 ADEF , AD ∩ DE = D , ∴ BH ⊥平面 ADEF . ∴ BH 是三棱锥 B - DEF 的高. 在Rt△ ABH 中,∠ BAD =60 ° , AB =2,故 BH =   . ∵ DE ⊥平面 ABCD , AD ⊂ 平面 ABCD ,∴ DE ⊥ AD . 由(1)知 BC ∥ EF ,又 AD ∥ BC , ∴ AD ∥ EF ,∴ DE ⊥ EF . ∴三棱锥 B - DEF 的体积 V =   S △ DEF · BH =   ×   × 1 × 1 ×   =   . 考点二    平面与平面平行的判定与性质 考向基础 　　平面与平面平行的判定和性质 性质 如果两个平面平行,则其中一个平面内的任一直线都平行于另一个平面(即面面平行 ⇒ 线面平行)     ⇒ a ∥ β 如果两个平行平面同时和第三个平面相交,那么它们的交线平行(即面面平行 ⇒ 线线平行)     ⇒ a ∥ b 如果两个平行平面中有一个平面垂直于一条直线,那么另一个平面也垂直于这条直线     ⇒ a ⊥ β 【知识拓展】 1.与平面平行有关的几个常用结论 (1)夹在两个平行平面之间的平行线段长度相等; (2)经过平面外一点有且只有一个平面与已知平面平行; (3)两条直线被三个平行平面所截,截得的对应线段成比例; (4)同一条直线与两个平行平面所成角相等. 2.平行问题的转化方向图 利用线线平行、线面平行、面面平行的相互转化解决平行关系的判定问 题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面 平行”,再到“面面平行”;而应用性质定理时,其顺序正好相反.在实际的 解题过程中,判定定理和性质定理一般要相互结合,灵活运用. 考向突破 考向一    证明平面与平面平行 例1　 如图,在长方体 ABCD - A 1 B 1 C 1 D 1 中, AB =1, AD =2, E , F 分别为 AD , AA 1 的中 点, Q 是 BC 上的一个动点,且 BQ = λQC ( λ >0). (1)当 λ =1时,求证:平面 BEF ∥平面 A 1 DQ ; (2)是否存在 λ ,使得 BD ⊥ FQ ?若存在,求出 λ 的值;若不存在,请说明理由.   解析 　(1)证明:当 λ =1时, Q 为 BC 的中点, 因为 E 是 AD 的中点, 所以 ED = BQ ,又 ED ∥ BQ ,所以四边形 BEDQ 是平行四边形,所以 BE ∥ QD . 又 BE ⊄ 平面 A 1 DQ , DQ ⊂ 平面 A 1 DQ ,所以 BE ∥平面 A 1 DQ . 又 F 是 A 1 A 的中点,所以 EF ∥ A 1 D . 因为 EF ⊄ 平面 A 1 DQ , A 1 D ⊂ 平面 A 1 DQ ,所以 EF ∥平面 A 1 DQ ,又 BE ∩ EF = E , 所以平面 BEF ∥平面 A 1 DQ . (2)存在.理由:如图,连接 AQ ,   因为 A 1 A ⊥平面 ABCD , BD ⊂ 平面 ABCD , 所以 A 1 A ⊥ BD . 又因为 BD ⊥ FQ , A 1 A 、 FQ ⊂ 平面 A 1 AQ ,且 A 1 A ∩ FQ = F ,所以 BD ⊥平面 A 1 AQ . 因为 AQ ⊂ 平面 A 1 AQ ,所以 AQ ⊥ BD . 在矩形 ABCD 中,由 AQ ⊥ BD ,得△ AQB ∽△ DBA , 所以 AB 2 = AD · BQ . 又 AB =1, AD =2,所以 BQ =   ,所以 QC =   , 所以   =   ,即 λ =   .故存在 λ =   满足题意. 考向二    平行关系中的存在性问题 例2     (2019四川内江质检三,18)如图,已知直角梯形 ACDE 所在的平面垂直 于平面 ABC ,∠ BAC =∠ ACD =90 ° ,∠ EAC =60 ° , AB = AC = AE . (1)在直线 BC 上是否存在一点 P ,使得 DP ∥平面 EAB ?请证明你的结论; (2)求平面 EBD 与平面 ABC 所成的锐二面角 θ 的余弦值.   解析 　(1)线段 BC 的中点就是满足条件的点 P .证明如下: 取 AB 的中点 F , BC 的中点 P ,连接 DP , PF , EF , 则 FP ∥ AC , FP =   AC . 取 AC 的中点 M ,连接 EM , EC . ∵ AE = AC 且∠ EAC =60 ° , ∴△ EAC 是正三角形. ∴ EM ⊥ AC . ∴四边形 EMCD 为矩形. ∴ ED = MC =   AC = FP . ∵ ED ∥ AC ,∴ ED ∥ FP ,∴四边形 EFPD 是平行四边形. ∴ DP ∥ EF . 又 EF ⊂ 平面 EAB , DP ⊄ 平面 EAB , ∴ DP ∥平面 EAB .   (2)过点 B 作 AC 的平行线 l ,过点 C 作 l 的垂线交 l 于点 G ,连接 DG , ∴四边形 ABGC 为矩形. ∵ ED ∥ AC ,∴ DE ∥ l . ∴ l 是平面 EBD 与平面 ABC 所成二面角的棱. ∵平面 EACD ⊥平面 ABC ,平面 EACD ∩ 平面 ABC = AC , DC ⊥ AC , ∴ DC ⊥平面 ABC . 又∵ l ⊂ 平面 ABC ,∴ DC ⊥ l . 又∵ CG ⊥ l , ∴ l ⊥平面 DGC ,∴ l ⊥ DG . ∴∠ DGC 是所求二面角的平面角. 设 AB = AC = AE =2 a , 则 CD =   a , GC =2 a . ∴ GD =   =   a . ∴cos θ =cos∠ DGC =   =   . 方法1      证明直线与平面平行的方法 1.利用线面平行的定义(此法一般伴随反证法证明). 2.利用线面平行的判定定理.应用此法的关键是在平面内找与已知直线平 行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑 三角形的中位线、平行四边形的对边等. 3.利用面面平行的性质:当两个平面平行时,其中一个平面内的任一直线都 平行于另一个平面. 方法技巧 例1 　正方形 ABCD 与正方形 ABEF 所在平面相交于 AB ,在 AE 、 BD 上各有 一点 P 、 Q ,且 AP = DQ .求证: PQ ∥平面 BCE . 解题导引   证明 证法一:如图所示,作 PM ∥ AB 交 BE 于 M ,作 QN ∥ AB 交 BC 于 N ,连接 MN . ∵正方形 ABCD 和正方形 ABEF 有公共边 AB ,∴ AE = BD . 又 AP = DQ ,∴ PE = QB , ∵ PM ∥ AB ∥ QN , ∴   =   =   ,   =   ,∴   =   , ∴ PM