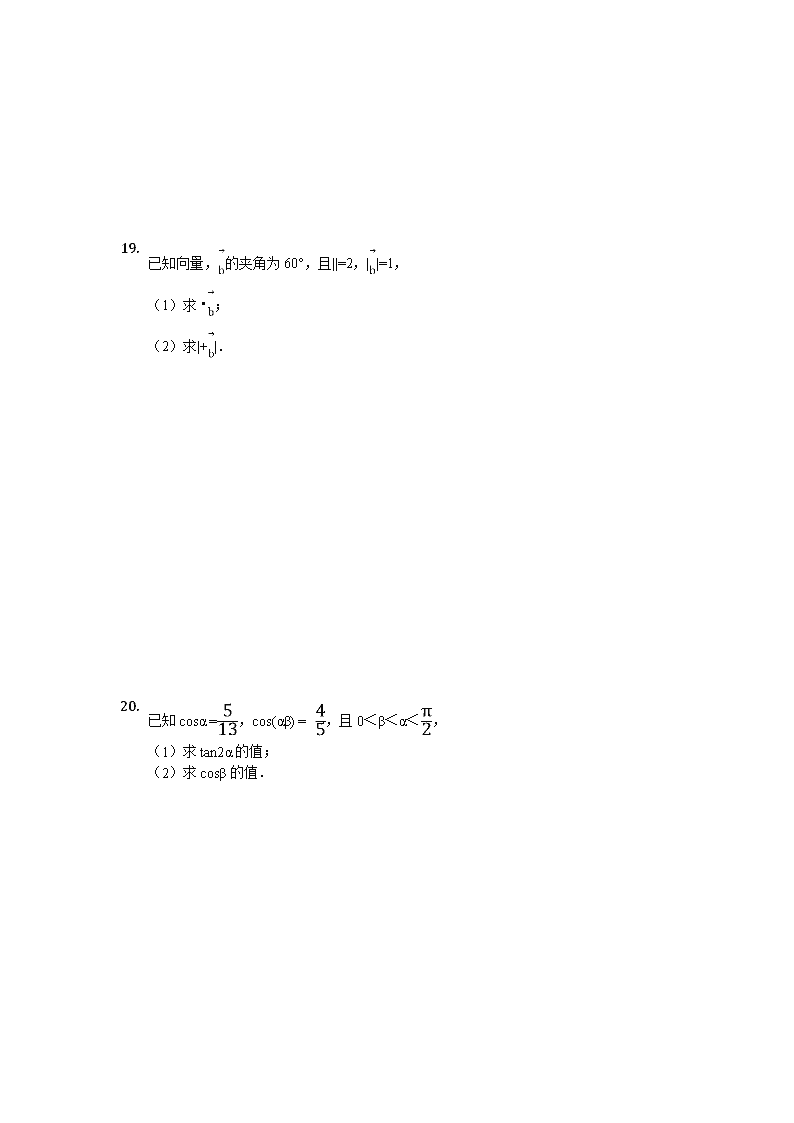2018-2019学年广西省桂林市中山中学高一下学期期中考试数学试卷 11页

‎ ‎ ‎2018-2019学年广西省桂林市中山中学高一下学期期中考试数学试卷 一、选择题（本大题共12小题，共60分）‎ 1. 把105°化为弧度为（　　）‎ A. B. C. D. ‎ 2. 若sinθ＞cosθ，且tanθ＜0，则角θ的终边位于（）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 3. 若α为第二象限角，sinα=，则cosα=（　　）‎ A. B. C. D. ‎ 4. 已知向量=（1，2），=（3，1），则-=（　　）‎ A. B. C. D. ‎ 5. 下列角的终边与37°角的终边在同一直线上的是（　　）‎ A. B. C. D. ‎ 6. 下列函数中，最小正周期为的是（　　）‎ A. B. C. D. ‎ 7. sin210°的值为（　　）‎ A. B. C. D. ‎ 8. 已知点A（1，1），B（3，5），若点C（-2，y）在直线AB上，则y的值是（　　）‎ A. B. C. 5 D. ‎ 9. 已知函数y=sin（2x+φ）的图象关于直线x=-对称，则φ的可能取值是（　　）‎ A. B. C. D. ‎ 10. 要得到y=sin（2x-）的图象，需要将函数y=sin2x的图象（　　）‎ A. 向左平移个单位 B. 向右平移个单位 C. 向左平移个单位 D. 向右平移个单位 11. 平面向量与的夹角为60°，=（1，），||=1，则||等于（　　）‎ A. B. C. 4 D. 12‎ 1. 函数f（x）=2sin（ωx+φ）（ω＞0，-＜φ＜）的部分图象如图所示，则ω，φ的值分别是（　　）‎ A. B. C. D. ‎ 二、填空题（本大题共4小题，共20分）‎ 2. tanα=，求=______．‎ 3. 若向量的夹角为60°，，则= ______ ．‎ 4. 若cosxcosy+sinxsiny=，则cos（2x-2y）= ______ ．‎ 5. 已知向量=（1，），=（-2，2），则与的夹角是______ ．‎ 三、解答题（本大题共6小题，共70.0分）‎ 6. 已知任意角α的终边经过点P（-3，m），且cosα=- （1）求m的值． （2）求sinα与tanα的值． ‎ 7. 已知f（α）=． （1）化简f（α）； （2）若tanα=2，且α∈（π，），求f（α）的值． ‎ ‎ ‎ 1. 已知向量，的夹角为60°，且||=2，||=1， （1）求 •；                   （2）求|+|． ‎ ‎ ‎ 2. 已知cosα =，cos(αβ) =，且0＜β＜α＜， （1）求tan2α的值；  （2）求cosβ的值． ‎ 1. 已知， ①若与垂直，求k的值； ②若与平行，求k的值． ‎ ‎ ‎ ‎22.已知函数f（x）=sin2ωx+sinωxsin（ωx+）（ω＞0）的最小正周期为π． （1）求ω的值； （2）求函数f（x）在区间[0，]上的取值范围．‎ ‎ 答案和解析 ‎1.【答案】C 【解析】‎ 解：因为180°=π弧度，所以1°=rad，所以105°=105×rad=rad； 故选：C． 根据弧度制的定义解答． 本题考查了弧度与角度的互化；1°=rad．1rad=．‎ ‎2.【答案】B 【解析】‎ 解：∵sinθ＞cosθ， ∴θ一定不再第四象限， 又tanθ＜0， ∴θ是第二或第四象限角， 可得θ是第二象限角， 故选B． 因为sinθ＞cosθ，可判断θ一定不是第四象限，又tanθ＜0，可得判断θ是第二或第四象限角，问题得以解决． 本题考查象限角的定义，熟练掌握三角函数在各个象限中的符号是解决问题的关键，属于基础题．‎ ‎3.【答案】A 【解析】‎ 解：∵α为第二象限角，且sinα=， ∴cosα=-=-． 故选：A． 由α为第二象限角，得到cosα小于0，根据sinα的值，利用同角三角函数间的基本关系即可求出cosα的值． 此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．‎ ‎4.【答案】B 【解析】‎ ‎【分析】 直接利用向量的减法的坐标运算求解即可．本题考查向量的坐标运算，基本知识的考查． 【解答】 解：∵向量=（1，2），=（3，1）， ∴-=（2，-1） 故选B．‎ ‎5.【答案】D 【解析】‎ 解：因为角的终边与37°角的终边在同一直线上的是37°+180°k，k是整数，k=-1时，37°-180°=-143°； ‎ 故选：D． 利用终边相同角的表示写出角的终边与37°角的终边在同一直线上的所有角，然后对k取值． 本题考查了三角函数的终边相同角的表示；与α在同一条直线的角为α+kπ，k∈Z．‎ ‎6.【答案】D 【解析】‎ 解：A、y=sinx，∵ω=1，∴T==2π，本选项错误； B、y=cosx，∵ω=1，∴T==2π，本选项错误； C、y=tan，∵ω=，∴T==2π，本选项错误； D、y=cos4x，∵ω=4，∴T==，本选项正确． 综上知，D选项正确． 故选：D． 找出C选项中的函数解析式中ω的值，代入周期公式T=，A，B，D三个选项解析式中ω的值，代入周期公式T=，分别求出各项的最小正周期，即可作出判断． 此题考查了三角函数的周期性及其求法，涉及的知识有正切函数及正弦函数的周期性，熟练掌握周期公式是解本题的关键，属于基础题．‎ ‎7.【答案】B 【解析】‎ 解：sin210°=sin（180°+30°）=-sin30°=-． 故选B 所求式子中的角度变形后，利用诱导公式化简即可求出值． 此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．‎ ‎8.【答案】A 【解析】‎ 解：点A（1，1），B（3，5），直线AB的方程为：， 即2x-y-1=0，点C（-2，y）在直线AB上， 看-4-y-1=0，解得y=-5． 故选：A． 求出直线AB的方程，代入C的坐标即可求解结果． 本题考查直线方程的求法与应用，基本知识的考查．‎ ‎9.【答案】A 【解析】‎ 解：函数y=sin（2x+φ）的图象关于直线x=-对称， ∴当x=-时，函数y取值最值，即sin（2×x+φ）=±1． 可得φ-=，k∈Z． ‎ ‎∴φ=． 当k=0时，可得φ=． 故选：A． 根据正弦函数的性质可知x=-时，函数y取值最值．即可求φ的可能取值． 本题考查正弦函数的对称轴性质的运用．属于基础题．‎ ‎10.【答案】D 【解析】‎ 解：将函数y=sin2x向右平移个单位，即可得到的图象，就是的图象； 故选：D． 由左加右减上加下减的原则可确定函数y=sin2x到的路线，进行平移变换，推出结果． 本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减．注意x的系数．‎ ‎11.【答案】B 【解析】‎ 解：平面向量与的夹角为60°，=（1，），||=1， 不妨可得=（1，0）， 则||=|（3，）|==2． 故选：B． 利用已知条件求出向量，然后利用坐标运算求解即可． 本题考查向量的模的求法，推出向量的坐标是简化解题的关键，考查计算能力．‎ ‎12.【答案】A 【解析】‎ 解：∵在同一周期内，函数在x=时取得最大值，x=时取得最小值， ∴函数的周期T满足=-=， 由此可得T==π，解得ω=2， 得函数表达式为f（x）=2sin（2x+φ） 又∵当x=时取得最大值2， ∴2sin（2•+φ）=2，可得+φ=+2kπ（k∈Z） ∵，∴取k=0，得φ=- 故选：A． ‎ 根据函数在同一周期内的最大值、最小值对应的x值，求出函数的周期T==π，解得ω=2．由函数当x=时取得最大值2，得到+φ=+kπ（k∈Z），取k=0得到φ=-．由此即可得到本题的答案． 本题给出y=Asin（ωx+φ）的部分图象，求函数的表达式．着重考查了三角函数的图象与性质、函数y=Asin（ωx+φ）的图象变换等知识，属于基础题．‎ ‎13.【答案】- 【解析】‎ 解：∵tanα=， ∴===-． 故答案为：- 所求式子分子分母同时除以cosα，利用同角三角函数间的基本关系弦化切后，将tanα的值代入计算即可求出值． 此题考查了同角三角函数基本关系的应用，以及同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．‎ ‎14.【答案】 【解析】‎ 解：， 故答案为． 用向量的数量积公式求值，将则展开后，用内积公式与求模公式求值． 考查内积公式及向量模的公式，属于向量里面的基本题型．‎ ‎15.【答案】- 【解析】‎ 解：∵cosxcosy+sinxsiny=cos（x-y）=， ∴cos（2x-2y）=cos2（x-y）=2cos2（x-y）-1=-． 故答案为：-． 已知等式左边利用两角和与差的余弦函数公式化简，求出cos（x-y）的值，所求式子利用二倍角的余弦函数公式化简后，将cos（x-y）的值代入计算即可求出值． 此题考查了两角和与差的余弦函数公式，二倍角的余弦函数公式，熟练掌握公式是解本题的关键．‎ ‎16.【答案】60° 【解析】‎ 解：∵=（1，），=（-2，2）， ∴||=2，||==4， •=-2+2×=6-2=4， 则cos＜，＞==， 则＜，＞=60°， 故答案为：60° 求出向量的长度和数量积，结合向量夹角公式进行求解即可． 本题主要考查向量数量积的应用，根据向量夹角公式是解决本题的关键．比较基础．‎ ‎17.【答案】解：（1）∵角α的终边经过点P（-3，m），∴|OP|=． 又∵cosα=-==，∴m2=16，∴m=±4． （2）m=4，得P（-3，4），|OP|=5，∴sinα=，tanα=-； m=-4，得P（-3，-4），|OP|=5，∴sinα=-，tanα=； 【解析】‎ ‎ （1）先求出|OP|，再利用cosα=-，即可求m的值． （2）分类讨论，即可求sinα与tanα的值． 本题考查同角三角函数基本关系的运用，考查三角函数的定义，比较基础．‎ ‎18.【答案】解：f（α）==cosα； （2）∵tanα=和sin2α+cos2α=1， ∴cos2α=． 又∵α∈（π，）， ∴cosα＜0， ∴f（α）=cosα=-． 【解析】‎ ‎ （1）利用诱导公式进行化简； （2）由tanα=和sin2α+cos2α=1求得cos2α的值，然后根据α的取值范围得到f（α）的值． 本题考查了同角三角函数基本关系的应用，三角函数的化简求值．三角函数式的化简要遵循“三看”原则： ‎ ‎（1）一看“角”，这是最重要的一环，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式． （2）二看“函数名称”，看函数名称之间的差异，从而确定使用的公式，常见的有“切化弦”； （3）三看“结构特征”，分析结构特征，可以帮助我们找到变形的方向，常见的有“遇到分式要通分”等．‎ ‎19.【答案】解：（1）×=||||cos60°=2×1×=1 （2）|+|2=（+）2 =+2•+ =4+2×1+1 =7 所以|+|= 【解析】‎ ‎ （1）由已知中，向量，的夹角为60°，且||=2，||=1，代入平面向量的数量积公式，即可得到答案． （2）由|+|2=（+）2，再结合已知中||=2，||=1，及（1）的结论，即可得到答案． 本题考查的知识点是平面向量数量积的坐标表示、模、及夹角，直接考查公式本身的直接应用，属基础题．‎ ‎20.【答案】解：（1）∵由cosα=，0＜α＜，得sinα===， ∴得tan= ∴于是tan2α==-． （2）由0＜β＜α＜，得0＜α-β＜， 又∵cos（α-β）=， ∴sin（α-β）==， 由β=α-（α-β）得： cosβ=cos[α-（α-β）]=cosαcos（α-β）+sinαsin（α-β）==． 【解析】‎ ‎ （1）利用已知及同角三角函数基本关系式可求sinα，进而可求tanα，利用二倍角的正切函数公式可求tan2α的值． （2）由0＜β＜α＜，得0＜α-β＜，利用同角三角函数基本关系式可求sin（α-β），由β=α-（α-β）利用两角差的余弦函数公式即可计算求值． 本题主要考查了三角函数基本关系式，二倍角的正切函数公式，两角差的余弦函数公式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．‎ ‎21.【答案】解：∵=（1，2）、 ∴， ①∵与垂直 ∴ 即10（k-3）-4（2k+2）=0 ∴k=19. ②∵与平行 ∴（k-3）×（-4）-（2k+2）×10=0 ∴. 【解析】‎ ‎ 由=（1，2），，知，． ①由与垂直，知10（k-3）-4（2k+2）=0，由此能求出k的值． ②由与平行，知（k-3）×（-4）-（2k+2）×10=0，由此能求出k的值． 本题考查平面向量垂直和平行的条件的应用，是基础题．解题时要认真审题，仔细解答．‎