2019届高三数学（文）二轮复习查漏补缺课时练习：（八）　第8讲　指数与指数函数 5页

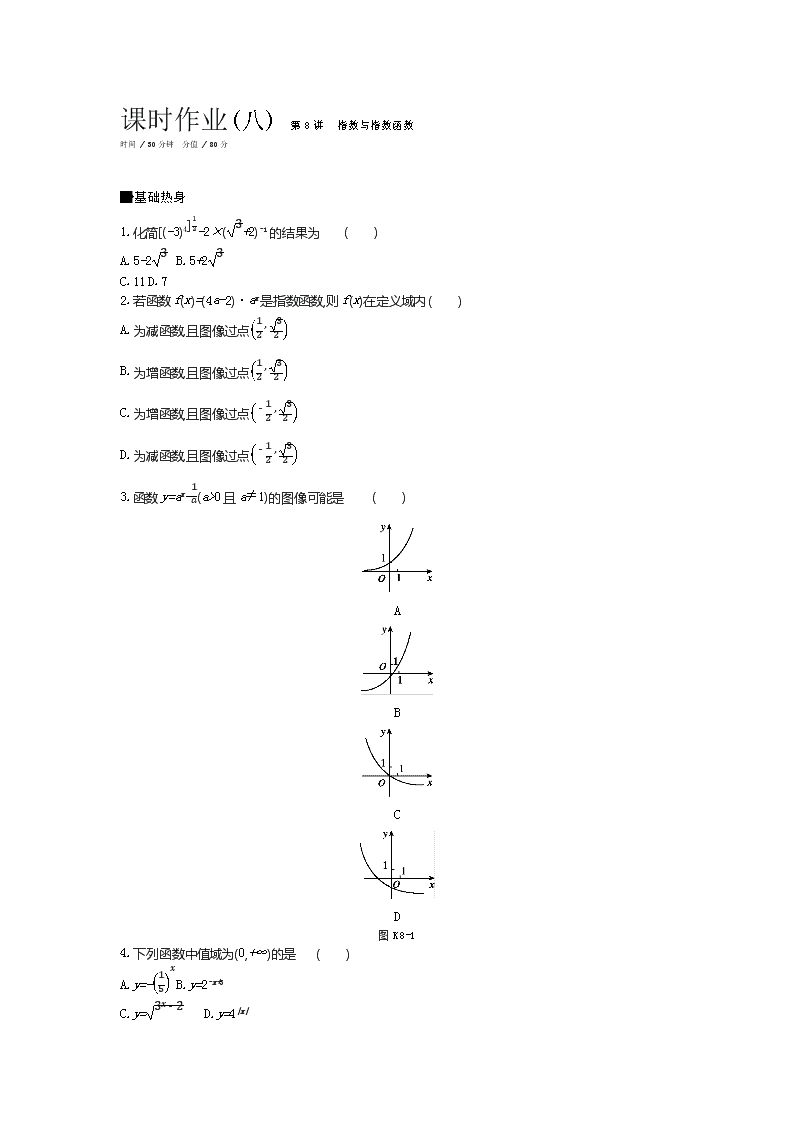
课时作业(八)　第8讲　指数与指数函数 时间 / 30分钟　分值 / 80分 ‎　　　　　　　　　　　　　　　　　　　‎ 基础热身 ‎1.化简[(-3)4‎]‎‎1‎‎2‎-2×(‎3‎+2)-1的结果为 (　　)‎ A.5-2‎3‎ B.5+2‎‎3‎ C.11 D.7‎ ‎2.若函数f(x)=(4a-2)·ax是指数函数,则f(x)在定义域内 (　　)‎ A.为减函数,且图像过点‎1‎‎2‎‎,‎‎3‎‎2‎ B.为增函数,且图像过点‎1‎‎2‎‎,‎‎3‎‎2‎ C.为增函数,且图像过点‎-‎1‎‎2‎,‎‎3‎‎2‎ D.为减函数,且图像过点‎-‎1‎‎2‎,‎‎3‎‎2‎ ‎3.函数y=ax-‎1‎a(a>0且a≠1)的图像可能是 (　　)‎ A B C D 图K8-1‎ ‎4.下列函数中值域为(0,+∞)的是 (　　)‎ A.y=-‎1‎‎5‎x B.y=2-x+3‎ C.y=‎3‎x‎-2‎ D.y=4|x|‎ ‎5.函数f(x)=‎2‎x‎-4‎‎3‎x‎-9‎的定义域为　　　　. ‎ 能力提升 ‎6.[2018·云南曲靖一模] 若a=‎1‎‎2‎‎3‎‎4‎,b=‎3‎‎4‎‎1‎‎2‎,c=log23,则a,b,c的大小关系是 (　　)‎ A.ag(x)‎ B.∀x∈(-∞,0),f(x)g(-x0)‎ D.∃x0∈(-∞,0),f(-x0)>g(x0)‎ ‎10.已知函数f(x)=ax(a>0且a≠1),如果以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,那么f(x1)·f(x2)等于 (　　)‎ A.1 B.a C.2 D.a2‎ ‎11.[2018·福州3月模拟] 设函数f(x)=‎0,x≤0,‎ex‎-e‎-x,x>0,‎则满足f(x2-2)>f(x)的x的取值范围是 (　　)‎ A.(-∞,-1)∪(2,+∞)‎ B.(-∞,-‎2‎)∪(‎2‎,+∞)‎ C.(-∞,-‎2‎)∪(2,+∞)‎ D.(-∞,-1)∪(‎2‎,+∞)‎ ‎12.当x<0,y<0时,化简:‎4‎‎16‎x‎8‎y‎4‎‎2x‎2‎y=　　　　. ‎ ‎13.已知函数f(x)=a2x-4+n(a>0且a≠1)的图像过定点P(m,2),则m+n=　　　　. ‎ ‎14.已知函数y=9x+m·3x-3在区间[-2,2]上单调递减,则m的取值范围为　　　　. 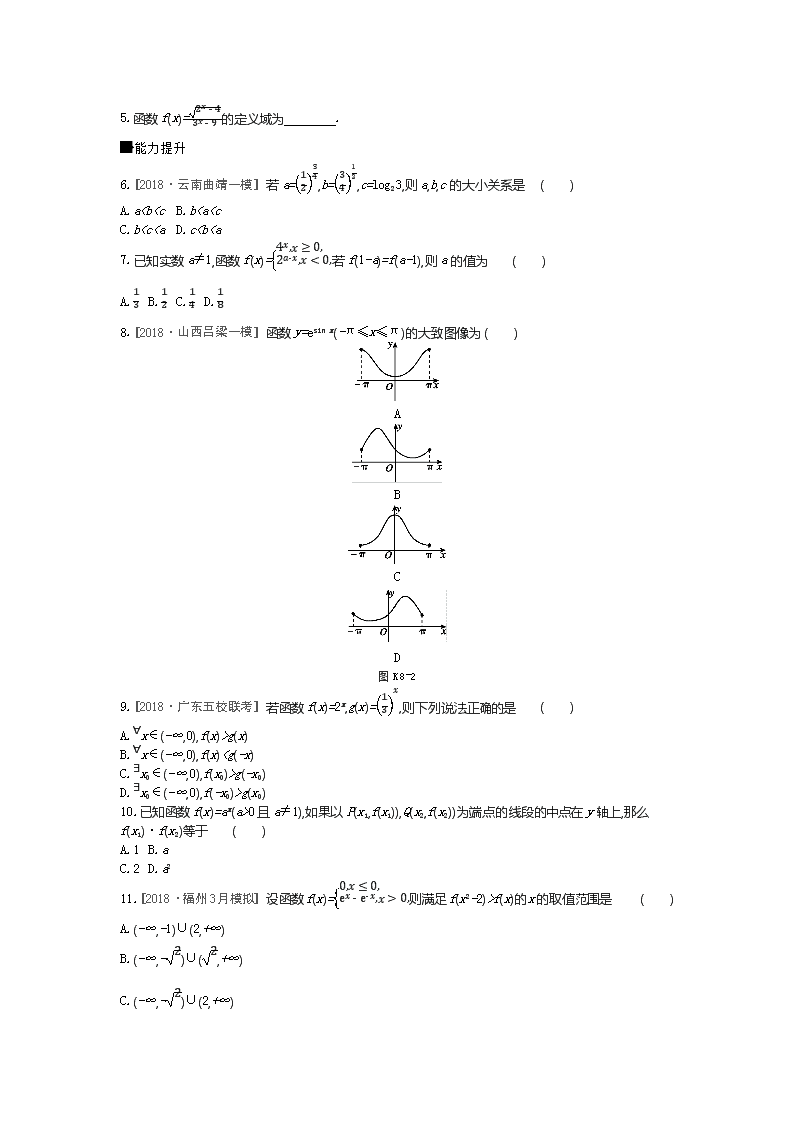‎ 难点突破 ‎15.(5分)[2018·沈阳模拟] 设函数f(x)是定义在R上的偶函数,且f(x+2)=f(2-x),当x∈[-2,0]时,f(x)=‎2‎‎2‎x-1,则在区间(-2,6)内关于x的方程f(x)-log8(x+2)=0的解的个数为 (　　)‎ A.1 B.2‎ C.3 D.4‎ ‎16.(5分)[2018·安徽淮南一模] 已知函数f(x)=e1+|x|-‎1‎‎1+‎x‎2‎,则使得f(x)>f(2x-1)成立的x的取值范围是　　　　. ‎ 课时作业(八)‎ ‎1.B　[解析] [(-3)4‎]‎‎1‎‎2‎-2×(‎3‎+2)-1=32-‎2‎‎2+‎‎3‎=9-2×(2-‎3‎)=5+2‎3‎.故选B.‎ ‎2.A　[解析] 由指数函数的定义知4a-2=1,解得a=‎3‎‎4‎,所以f(x)=‎3‎‎4‎x,所以f(x)在定义域内为减函数,且f‎1‎‎2‎=‎3‎‎2‎.故选A.‎ ‎3.D　[解析] 当01,函数y=ax-‎1‎a是减函数,且其图像是由函数y=ax的图像向下平移‎1‎a个单位长度得到的,故选D.‎ ‎4.B　[解析] y=-‎1‎‎5‎x的值域为(-∞,0);因为-x+3∈R,所以y=2-x+3的值域为(0,+∞);y=‎3‎x‎-2‎的值域为[0,+∞);y=4|x|的值域为[1,+∞).故选B.‎ ‎5.(2,+∞)　[解析] 要使函数f(x)有意义,则2x-4≥0且3x-9≠0,解得x>2,所以函数f(x)的定义域为(2,+∞).‎ ‎6.A　[解析] 由a=‎1‎‎2‎‎3‎‎4‎得a4=‎1‎‎8‎,由b=‎3‎‎4‎‎1‎‎2‎得b4=‎9‎‎16‎,所以b4>a4>0,又0log22=1,所以a1时,4a-1=2a-(1-a),无解.故选B.‎ ‎8.D　[解析] 易知函数y=esin x(-π≤x≤π)不是偶函数,排除A,C;当x∈‎-π‎2‎,‎π‎2‎时,y=sin x为增函数,而函数y=ex也是增函数,所以y=esin x(-π≤x≤π)在‎-π‎2‎,‎π‎2‎上为增函数,故选D.‎ ‎9.C　[解析] 因为f(-1)=‎1‎‎2‎,g(-1)=3,f(-1)g(1),所以B中说法错误,C中说法正确;因为当x<0时,‎1‎‎2‎x<‎1‎‎3‎x,所以D中说法错误.故选C.‎ ‎10.A　[解析] 因为以P(x1,f(x1)),Q(x2,f(x2))为端点的线段的中点在y轴上,所以x1+x2=0.又因为f(x)=ax,所以f(x1)·f(x2)=ax‎1‎·ax‎2‎=ax‎1‎‎+‎x‎2‎=a0=1.‎ ‎11.C　[解析] x>0时,f(x)=ex-e-x是增函数,x≤0时,f(x)=0为常函数,且f(0)=0,所以由f(x2-2)>f(x)得x2-2>x>0或x2-2>0>x,解得x>2或x<-‎2‎.故选C.‎ ‎12.-1　[解析] ‎4‎‎16‎x‎8‎y‎4‎‎2x‎2‎y=‎(16‎x‎8‎y‎4‎‎)‎‎1‎‎4‎‎2x‎2‎y=‎2·(-x‎)‎‎2‎·(-y)‎‎2x‎2‎y=-1.‎ ‎13.3　[解析] 当2x-4=0,即x=2时,f(x)=1+n,即函数f(x)的图像恒过点(2,1+n),又函数图像过定点P(m,2),所以m=2,1+n=2,即m=2,n=1,所以m+n=3.‎ ‎14.m≤-18　[解析] 设t=3x,则y=t2+mt-3,因为x∈[-2,2],所以t∈‎1‎‎9‎‎,9‎.‎ 又因为y=9x+m·3x-3在区间[-2,2]上单调递减,y=3x在[-2,2]上单调递增,所以y=t2+mt-3在‎1‎‎9‎‎,9‎上单调递减,得-m‎2‎≥9,解得m≤-18.‎ ‎15.C　[解析] 因为f(x)是定义在R上的偶函数,且f(x+2)=f(2-x),所以f(x+4)=f(-x)=f(x),所以函数f(x)是一个周期函数,且周期为4.因为f(x)-log8(x+2)=0,所以f(x)=log8(x+2),则方程f(x)-log8(x+2)=0的解的个数即为曲线y=f(x)与y=log8(x+2)的交点个数.由当x∈[-2,0]时,f(x)=‎2‎‎2‎x-1,且函数f(x)是定义在R上的偶函数,作出y=f(x)与y=log8(x+2)在区间(-2,6)内的图像,如图所示,显然交点个数为3.故选C.‎ ‎16.‎1‎‎3‎‎,1‎　[解析] 因为函数f(x)=e1+|x|-‎1‎‎1+‎x‎2‎满足f(-x)=f(x),所以函数f(x)为偶函数.当x≥0时,y=e1+x为增函数,y=‎1‎‎1+‎x‎2‎为减函数,故函数f(x)在x≥0时为增函数,在x<0时为减函数,则由f(x)>f(2x-1)得|x|>|2x-1|,即x2>4x2-4x+1,解得‎1‎‎3‎