数学理卷·2017届河北省衡水市冀州中学高三（高复班）上学期12月月考（2016 8页

河北冀州中学 ‎2016—2017学年度上学期第四次月考 高三年级理科数学试题 考试时间120分钟 试题分数150分 第I卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1、设集合，集合，若，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎2、已知（其中均为实数，为虚数单位），则等于（ ）‎ A．2 B．1 C． D．1或 ‎3、设，都是非零向量，那么命题“与共线”是命题“|+|=||+||”的（　　）‎ A．充分不必要条件B．必要不充分条件C．充要条件D．非充分非必要条件 ‎4、已知实数满足不等式组，则（　　）‎ ‎ A. 的最大值为4，无最小值 B. 的最大值为4，最小值为1 ‎ ‎ C. 的最大值为1，无最小值 D. 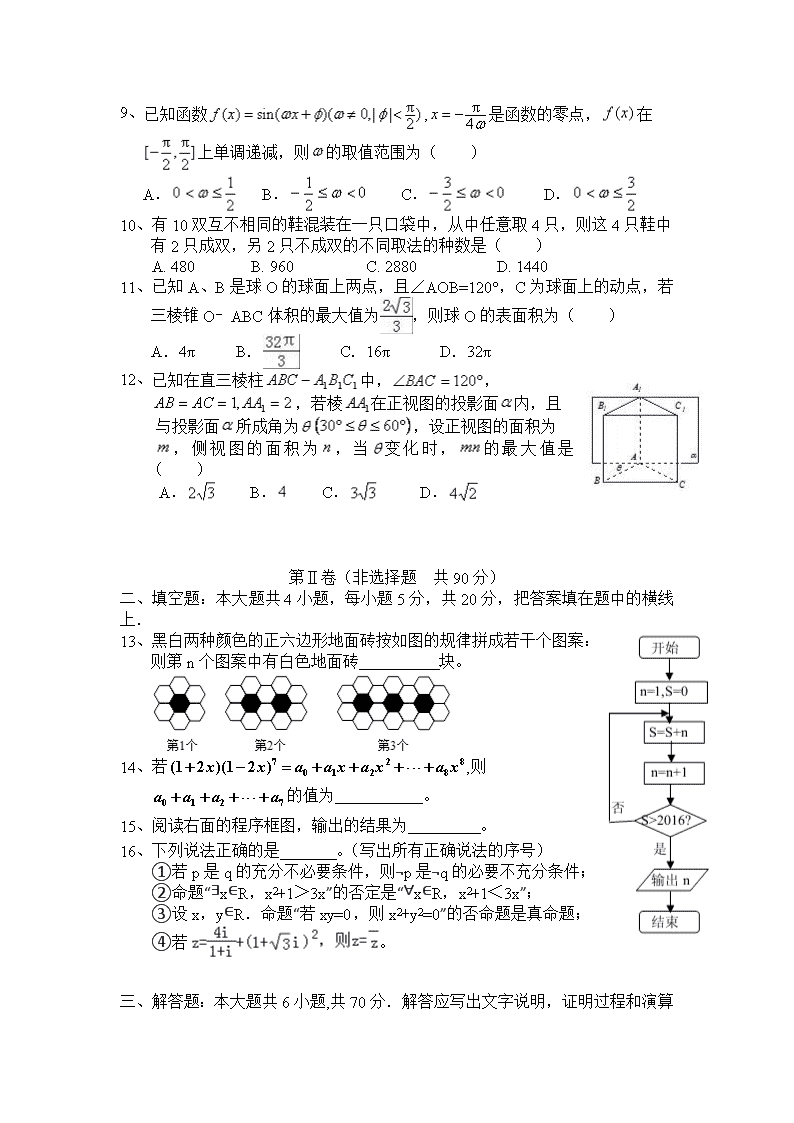的最小值为1，无最大值 ‎5、设公差不为零的等差数列的前项和为，若，则等于 A． B． C．7 D．14（ ）‎ ‎6、已知正六边形ABCDEF中，P，Q，R分别是边AB，EF，‎ CD的中点，则向正六边形ABC－DEF内投掷一点，该点 落在△PQR内的概率为（ ）‎ ‎ A、 B、 C、 D、‎ ‎7、已知，随机变量的分布列如下，则当a增大时（ ）‎ ‎－1‎ ‎0‎ ‎1‎ P ‎ A、增大，增大 B、减小，增大 ‎ C、增大，减小 D、减小，减小 ‎8、已知，则的值为 ‎ A、 B、 C、 D、‎ ‎9、已知函数,是函数的零点，在上单调递减，则的取值范围为（   ）‎ A． B． C． D．‎ ‎10、有10双互不相同的鞋混装在一只口袋中，从中任意取4只，则这4只鞋中有2只成双，另2只不成双的不同取法的种数是（ ）‎ ‎ A. 480 B. 960 C. 2880 D. 1440‎ ‎11、已知A、B是球O的球面上两点，且∠AOB=120°，C为球面上的动点，若三棱锥O﹣ABC体积的最大值为，则球O的表面积为（　　）‎ A．4π B． C．16π D．32π ‎12、已知在直三棱柱中，，‎ ‎，若棱在正视图的投影面内，且 与投影面所成角为，设正视图的面积为 ‎，侧视图的面积为，当变化时，的最大值是（   ）‎ A． B． C． D．‎ ‎ ‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中的横线上．‎ ‎13、黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：‎ 则第n个图案中有白色地面砖　 　块。‎ ‎14、若,则 的值为 。‎ ‎15、阅读右面的程序框图，输出的结果为 。‎ ‎16、下列说法正确的是 。（写出所有正确说法的序号）‎ ‎①若p是q的充分不必要条件，则¬p是¬q的必要不充分条件；‎ ‎②命题“∃x∈R，x2+1＞3x”的否定是“∀x∈R，x2+1＜3x”；‎ ‎③设x，y∈R．命题“若xy=0，则x2+y2=0”的否命题是真命题；‎ ‎④若。‎ 三、解答题：本大题共6小题,共70分．解答应写出文字说明，证明过程和演算步骤．‎ ‎17、（本小题满分10分）‎ 已知函数的最大值为．　‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）若，求的最大值．‎ ‎18、（本小题满分12分）‎ 某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，远离毒品”的电视公益广告，期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段在，，，，的市民进行问卷调查，由此得到样本占有率分布直方图如图所示.‎ ‎（Ⅰ）求随机抽取的市民中年龄在的人数；‎ ‎（Ⅱ）从不小于40岁的人中按年龄段分层抽样的方法随 机抽取5人，求年龄段抽取样品的人数；‎ ‎（Ⅲ）从（Ⅱ）中方式得到的5人中再选取2人作为本次 活动的获奖者，记X为年龄在年龄段的人 数，求X的分布列及数学期望。‎ ‎19、（本小题满分12分）‎ 在△ABC中，a，b，c分别为A，B，C所对的边，且。‎ ‎（Ⅰ）求角A的大小；（Ⅱ）若△ABC的面积为3，求a的值。‎ ‎20、（本小题满分12分）‎ 已知数列{an}的前n项和为Sn，若a1=1，且Sn=tan﹣，其中n∈N*．‎ ‎（Ⅰ）求实数t的值和数列{an}的通项公式；‎ ‎（Ⅱ）若数列{bn}满足bn=log3a2n，求数列{}的前n项和Tn．‎ ‎21、（本小题满分12分）‎ 已知三棱柱ABC﹣A1B1C1中，侧面ABB1A1为正方形，延长AB到D，使得AB=BD，平面AA1C1C⊥平面ABB1A1，A1C1=AA1，∠C1A1A=．‎ ‎（Ⅰ）若E，F分别为C1B1，AC的中点，求证：EF∥平面ABB1A1；‎ ‎（Ⅱ）求平面A1B1C1与平面CB1D所成的锐二面角的余弦值．‎ ‎22、（本小题满分12分）‎ 已知数列{an}为等比数列，其前n项和为Sn ，若a 1+a4 =，且对于任 ‎ 意的n∈N** 有Sn，Sn+2 ，S n+1 成等差数列。‎ ‎（1）求数列{a}的通项公式；‎ ‎（2）已知bn=n（n∈N* ），记Tn =，若(n－1)2≤m(Tn –n－1)对于n≥2恒成立，求实数m的范围。‎ 高三年级第次月考理科数学试题 一、选择题：BCBDCB BCBDCC 二、填空题：13、4n+2； 14、253； 15、65；16、①③ ‎ 三、解答题：‎ ‎17、解：（1）由于，所以．．．．5分 ‎（2）由已知，有，‎ 因为（当取等号），（当取等号），‎ 所以，即，‎ 故．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分 ‎18、解：（Ⅰ）（1）当n=1时，a1=S1=ta1﹣，由a1=1，即1=t﹣，解得：t=，‎ ‎∴Sn=•an﹣， 当n≥2时，Sn﹣1=•an﹣1﹣，‎ ‎∴an=Sn﹣Sn﹣1=（•an﹣）﹣（•an﹣1﹣），即an=3an﹣1，‎ ‎∴数列{an}是以1为首项，以3为公比的等比数列，∴an=a1•qn﹣1=3n﹣1，‎ 当n=1时，an=3n﹣1，成立，∴数列{an}的通项公式an=3n﹣1；‎ ‎（Ⅱ）由（1）可知：bn=log3a2n=log332n﹣1=2n﹣1，‎ ‎==（﹣），‎ 则Tn=（1﹣）+（﹣）+…+（﹣），‎ ‎=（1﹣+﹣+…+﹣）=（1﹣）=，‎ 所以数列{}的前n项和Tn=．‎ ‎19、解：（1）由已知可得：，即，‎ ‎∴tanB = 2tanA，tanC = 3tanA。由tanA = － tan（B + C）得tanA=1，‎ ‎∴A = 45°。……6分 ‎（2）由（1）知tanA=1，tanB=2，tanC=3，则，，，‎ 由正弦定理可得：，，由=3得。……12分 ‎20、解　（Ⅰ）由题意知，ξ的所有可能取值为0，10，20，30.‎ ‎ P(ξ＝0)＝××＝，‎ P(ξ＝10)＝××＋××＋××＝＝，‎ P(ξ＝20)＝××＋××＋××＝＝，‎ P(ξ＝30)＝××＝＝.‎ ξ的分布列为：‎ ξ ‎0‎ ‎10‎ ‎20‎ ‎30‎ P ‎ ‎ ∴E(ξ)＝0×＋10×＋20×＋30×＝.‎ ‎（Ⅱ）用A表示“甲得30分乙得0分”，用B表示“甲得20分乙得10分”，且A，B互斥.‎ 又P(A)＝×＝，‎ P(B)＝C××＝，‎ 甲、乙两人得分总和为30分且甲获胜的概率为 P(A＋B)＝P(A)＋P(B)＝＝.‎ ‎21、证明：（Ⅰ）取A1C1的中点G，连结FG，EG，‎ 在△A1B1C1中，EG为中位线，∴EG∥A1B1，‎ ‎∴GE⊄平面ABB1A1，A1B1⊂平面ABB1A1，‎ ‎∴GE∥ABB1A1，同理得GF∥平面ABB1A1，‎ 又GF∩GE=G，∴平面GEF∥平面ABB1A1，‎ ‎∵EF⊂平面GEF，∴EF∥平面ABB1A1．‎ 解：（Ⅱ）连结AC1，在△AA1C1中，，，‎ ‎∴由余弦定理得=+﹣2AA1×A1C1cos∠AA1C1=，‎ ‎∴AA1=AC1，△A1AC1是等腰直角三角形，AC1⊥AA1，‎ 又∵平面AA1C1C∩平面ABB1A1=AA1，‎ ‎∴AC1⊥平面ABB1A1，‎ ‎∵AB⊂平面ABB1A1，∴AC1⊥AB，‎ 又∵侧面ABB1A1为正方形，∴AA1⊥AB，‎ 分别以AA1，AB，AC1所在直线为x轴，y轴，z轴，建立空间直角坐标系，‎ 设AB=1，则A（0，0，0），A1（1，0，0），B1（1，1，0），‎ C1（0，0，1），C（﹣1，0，1），D（0，2，0），‎ ‎∴=（2，1，﹣1），=（1，2，﹣1），=（﹣1，0，1），=（0，1，0），‎ 设平面A1B1C1的法向量=（x，y，z），‎ 则，取x=1，得=（1，0，1），‎ 设平面CB1D的法向量=（a，b，c），‎ 则，取a=1，得=（1，1，3），‎ cos＜＞===，‎ ‎∴平面A1B1C1与平面CB1D所成的锐二面角的余弦值为．‎ ‎22、解：（1）‎ ‎…………4分 ‎（2） ， ‎ ‎ ‎ ‎ …………8分 若对于恒成立，则，‎ ‎，，‎ 令，‎ 所以为减函数， …………12分