- 294.00 KB
- 2021-06-22 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1、核心内容:
三视图的长度特征——“长对齐,宽相等,高平齐”,即正视图和左视图一样高,正视图和俯视图一样长,左视图和俯视图一样宽。
2、还原三步骤:
(1)先画正方体或长方体,在正方体或长方体地面上截取出俯视图形状;
(2)依据正视图和左视图有无垂直关系和节点,确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条(剔除其中无需垂直拉升的节点,不能确定的先垂直拉升),由高平齐确定其长短;
(3)将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线,隐去所有的辅助线条便可得到还原的几何体。
3、还原方法详解
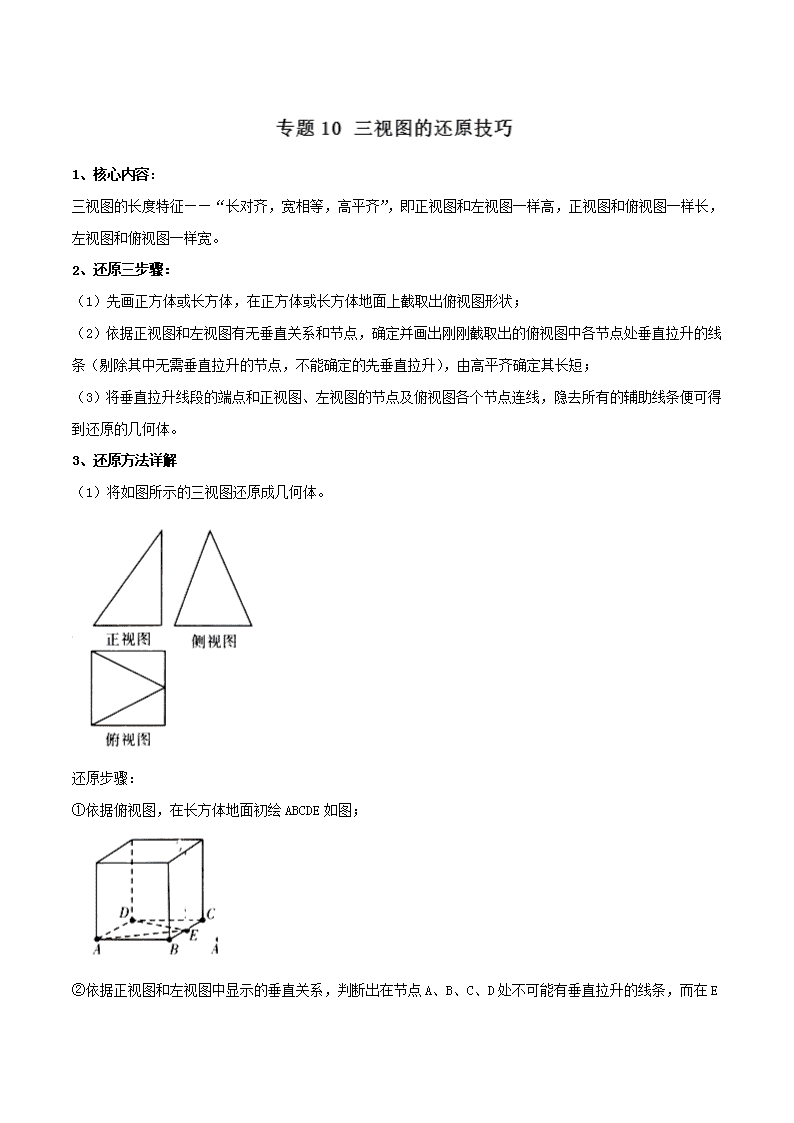
(1)将如图所示的三视图还原成几何体。
还原步骤:
①依据俯视图,在长方体地面初绘ABCDE如图;
②依据正视图和左视图中显示的垂直关系,判断出在节点A、B、C、D处不可能有垂直拉升的线条,而在E
处必有垂直拉升的线条ES,由正视图和侧视图中高度,确定点S的位置;
如图
③将点S与点ABCD分别连接,隐去所有的辅助线条,便可得到还原的几何体S-ABCD如图所示:
4、典型例题:
例1:若某几何体的三视图,如图所示,则此几何体的体积等于( )cm³。
【答案】24
【解析】
根据上述步骤,还原几何体可得AD-BCMN,则
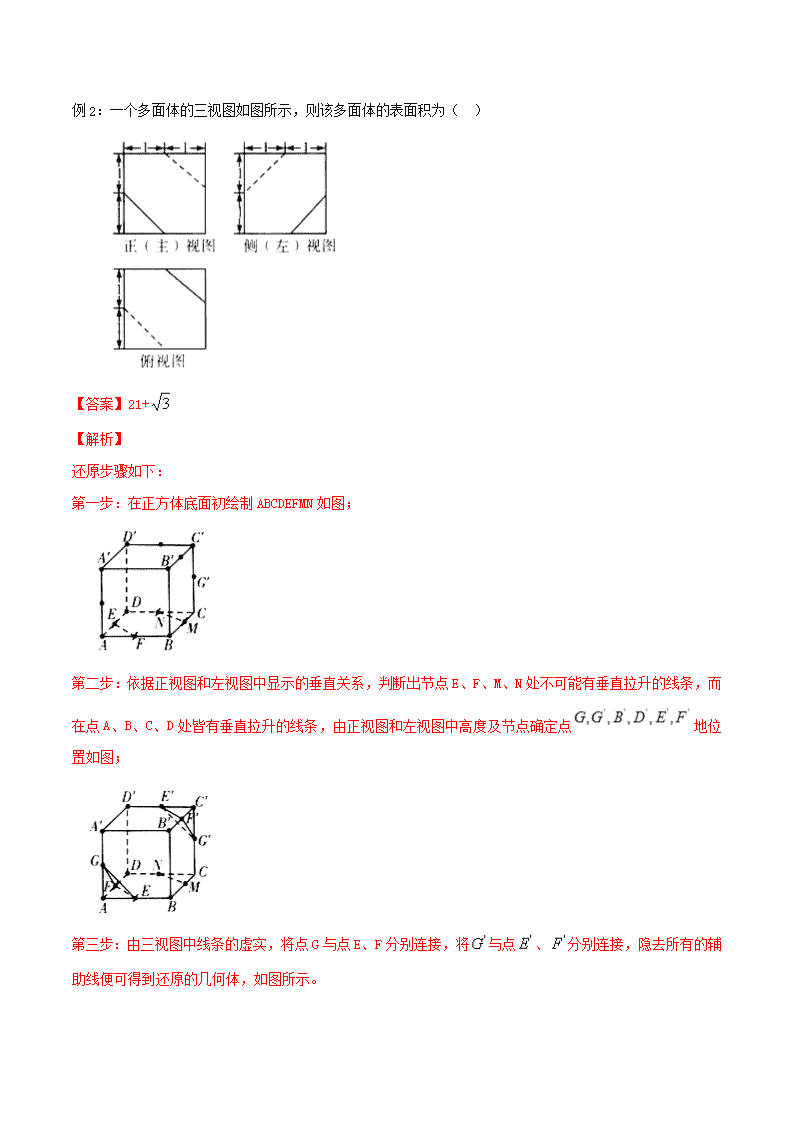
例2:一个多面体的三视图如图所示,则该多面体的表面积为( )
【答案】21+
【解析】
还原步骤如下:
第一步:在正方体底面初绘制ABCDEFMN如图;
第二步:依据正视图和左视图中显示的垂直关系,判断出节点E、F、M、N处不可能有垂直拉升的线条,而在点A、B、C、D处皆有垂直拉升的线条,由正视图和左视图中高度及节点确定点地位置如图;
第三步:由三视图中线条的虚实,将点G与点E、F分别连接,将与点、分别连接,隐去所有的辅助线便可得到还原的几何体,如图所示。
则表面积为。
例3:如图所示,网格纸上小正方形的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )
【答案】6
【解析】
还原图形方法1:
若由主视图引发,具体步骤如下:
(1)依据主视图,在长方体后侧面初绘ABCM如图:
(2)依据俯视图和左视图中显示的垂直关系,判断出在节点A、B、C出不可能有垂直向前拉升的线条,而在M出必有垂直向前拉升的线条MD,由俯视图和侧视图中长度,确定点D的位置如图:
(3)将点D与A、B、C分别连接,隐去所有的辅助线条便可得到还原的几何体D—ABC如图所示:
置于棱长为4个单位的正方体中研究,该几何体为四面体D—ABC,且AB=BC=4,AC=,DB=DC=,可得DA=6.故最长的棱长为6.
方法2:
若由左视图引发,具体步骤如下:
(1)依据左视图,在长方体右侧面初绘BCD如图:
(2)依据正视图和俯视图中显示的垂直关系,判断出在节点C、D处不可能有垂直向前拉升的线条,而在B处,必有垂直向左拉升的线条BA,由俯视图和左视图的长度,确定点A的位置,如图:
(3)将点A与点B、C、D分别连接,隐去所有的辅助线条便可得到还原的几何体D—ABC如图:
方法3:
由三视图可知,原几何体的长、宽、高均为4,所以我们可以用一个正方体做载体还原:
(1)根据正视图,在正方体中画出正视图上的四个顶点的原象所在的线段,用红线表示。如图,也就是说正视图的四个顶点必定是由原图中红线上的点投影而成;
(2)左视图有三个顶点,画出它们的原象所在的线段,用蓝线表示,如图;
(3)俯视图有三个顶点,画出它们的原象所在的线段,用绿线表示,如图;
(4)三种颜色的公共点(一定要三种颜色公共交点)即为几何体的顶点,连接各顶点即为原几何体,如图。然后计算出最长的棱。
【掌握练习】
1、一个棱锥的三视图如图,则该棱锥的表面积(单位:)为________.
【答案】
2、已知某三棱锥的三视图如图所示,则该三棱锥的体积是________.
【答案】
【解析】
由三视图可得三棱锥如图所示,则.
3、—锥体的三视图如图所示,则该棱锥的最长棱的棱长为________.
【答案】
4、已知某几何体的三视图如图所示,则该几何体的各侧面中,面积最小值等于________.
【答案】