数学卷·2018届湖北省宜昌市西陵区金东方高中高二下学期第一次月考数学试卷（理科） （解析版） 22页

‎2016-2017学年湖北省宜昌市西陵区金东方高中高二（下）第一次月考数学试卷（理科）‎ ‎　‎ 一、选择题（本大题共12小题，每小题5分，满分60分）‎ ‎1．当＜m＜1时，复数m（3+i）﹣（2+i）在复平面内对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．在空间四边形OABC中，，，，点M在线段OA上，且OM=2MA，N为BC的中点，则等于（　　）‎ A． ﹣+ B．﹣++ C． D．‎ ‎3．执行如图所示的程序框图．若n=5，则输出s的值是（　　）‎ A．﹣21 B．11 C．43 D．86‎ ‎4．双曲线x2﹣my2=1的实轴长是虚轴长的2倍，则m等于（　　）‎ A． B． C．2 D．4‎ ‎5．已知命题p：“∀x∈R时，都有”； 命题q：“∃x°∈R，使sinx°+cosx°=2时”，则下列判断正确的是（　　）‎ A．p∨q为假命题 B．p∧q为真命题 C．￢p∧q为真命题 D．￢p∨￢q为假命题 ‎6．已知m，n表示两条不同直线，α表示平面，下列说法正确的是（　　）‎ A．若m∥α，n∥α，则m∥n B．若m⊥α，n⊂α，则m⊥n C．若m⊥α，m⊥n，则n∥α D．若m∥α，m⊥n，则n⊥α ‎7．若实数a，b满足a2+b2≤1，则关于x的方程x2﹣2x+a+b=0有实数根的概率是（　　）‎ A． B． C． D．‎ ‎8．设n=4sinxdx，则（x+）（x﹣）n的展开式中各项系数和为（　　）‎ A．1 B．2 C．3 D．4‎ ‎9．在三棱锥P﹣ABC中，△ABC为等边三角形，PA⊥平面ABC，且PA=AB，则二面角A﹣PB﹣C的平面角的正切值为（　　）‎ A． B． C． D．‎ ‎10．若函数f（x）=x2+ax+在（，+∞）上是增函数，则a的取值范围是（　　）‎ A．[﹣1，0] B．[﹣1，+∞） C．[0，3] D．[3，+∞）‎ ‎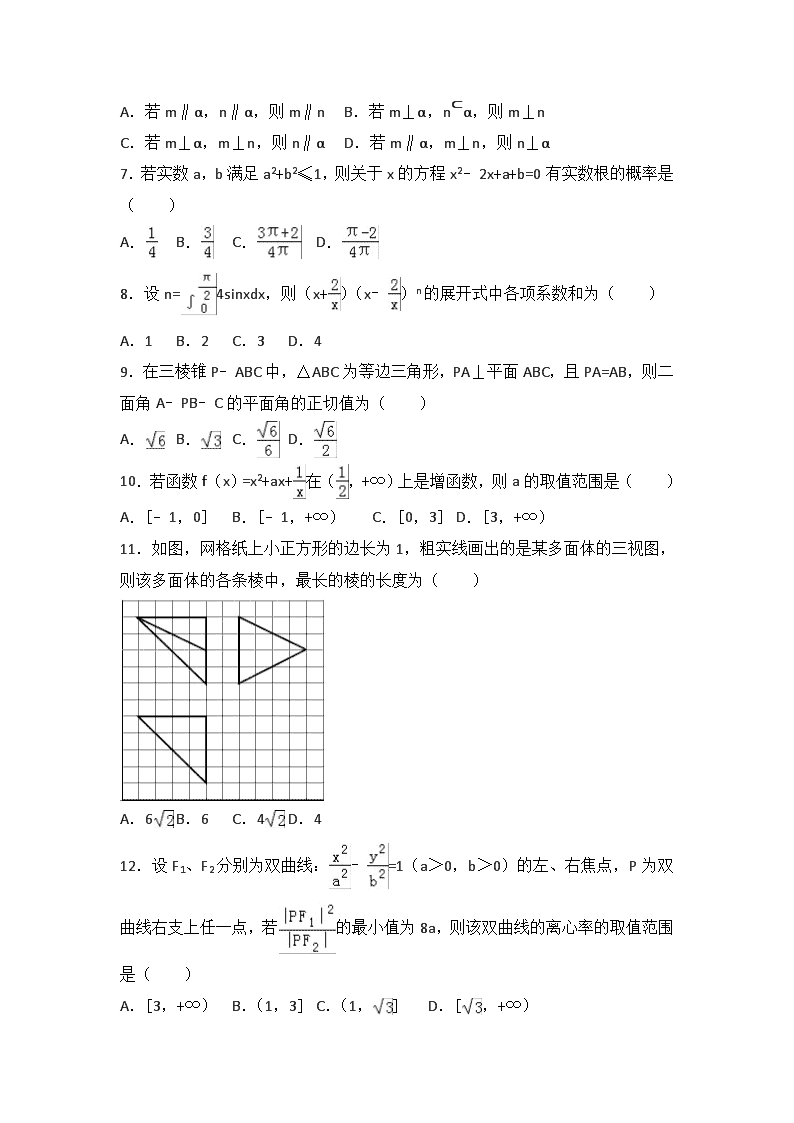11．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（　　）‎ A．6 B．6 C．4 D．4‎ ‎12．设F1、F2分别为双曲线：﹣=1（a＞0，b＞0）的左、右焦点，P为双曲线右支上任一点，若的最小值为8a，则该双曲线的离心率的取值范围是（　　）‎ A．[3，+∞） B．（1，3] C．（1，] D．[，+∞）‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，满分20分）.‎ ‎13．（x3+）7的展开式中的x5的系数是　　（用数字填写答案）‎ ‎14．若命题“∀x∈R，ax2+2x+1＞0”为真命题，则a的取值范围为　　．‎ ‎15．过点（﹣4，0）作直线L与圆x2+y2+2x﹣4y﹣20=0交于A、B两点，如果|AB|=8，则L的方程为　　．‎ ‎16．如图，把椭圆的长轴AB分成8等份，过每个分点作x轴的垂线交椭圆的上半部分于P1，P2，P3，P4，P5，P6，P7七个点，F是椭圆的一个焦点则|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=　　．‎ ‎　‎ 三、解答题（本大题共6小题，满分70分）‎ ‎17．已知p：2x2﹣3x﹣2≥0，q：x2﹣（2a﹣2）x+a（a﹣2）≥0，若p是q的充分不必要条件．求实数a的取值范围．‎ ‎18．某同学在篮球场上进行投篮训练，先投“2分的篮”2次，每次投中的概率为，每投中一次得2分，不中得0分；再投“3分的篮”1次，每次投中的概率为，投中得3分，不中得0分，该同学每次投篮的结果相互独立，假设该同学要完成以上三次投篮．‎ ‎（1）求该同学恰好有2次投中的概率；‎ ‎（2）求该同学所得分X的分布列．‎ ‎19．如图，直三棱柱ABC﹣A1B1C1中，△ABC是等边三角形，D是BC的中点．‎ ‎（1）求证：A1B∥平面ADC1；‎ ‎（2）若AB=BB1，求A1D与平面ADC1所成角的正弦值．‎ ‎20．某校举行运动会，其中三级跳远的成绩在8.0米 （四舍五入，精确到0.1米） 以上的进入决赛，把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．‎ ‎（1）求进入决赛的人数；‎ ‎（2）经过多次测试后发现，甲成绩均匀分布在8～10米之间，乙成绩均匀分布在9.5～10.5米之间，现甲，乙各跳一次，求甲比乙远的概率．‎ ‎21．已知抛物线C：y2=2px（p＞0）的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有|FA|=|FD|．当点A的横坐标为3时，△ADF为正三角形．‎ ‎（1）求C的方程；‎ ‎（2）若直线l1∥l，且l1和C有且只有一个公共点E，证明直线AE过定点，并求出定点坐标．‎ ‎22．设函数f（x）=﹣k（+lnx）（k为常数，e=2.71828…是自然对数的底数）．‎ ‎（Ⅰ）当k≤0时，求函数f（x）的单调区间；‎ ‎（Ⅱ）若函数f（x）在（0，2）内存在两个极值点，求k的取值范围．‎ ‎　‎ ‎2016-2017学年湖北省宜昌市西陵区金东方高中高二（下）第一次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，每小题5分，满分60分）‎ ‎1．当＜m＜1时，复数m（3+i）﹣（2+i）在复平面内对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【考点】复数的代数表示法及其几何意义．‎ ‎【分析】化简成代数形式，再根据m的范围确定．‎ ‎【解答】解：化简得（3m﹣2）+i（m﹣1），‎ 又∵‎ ‎∴3m﹣2＞0，m﹣1＜0‎ ‎∴所对应的点在第四象限 故选D．‎ ‎　‎ ‎2．在空间四边形OABC中，，，，点M在线段OA上，且OM=2MA，N为BC的中点，则等于（　　）‎ A． ﹣+ B．﹣++ C． D．‎ ‎【考点】向量加减混合运算及其几何意义．‎ ‎【分析】由题意结合图形，直接利用，求出，然后即可解答．‎ ‎【解答】解：因为空间四边形OABC如图，，，，‎ 点M在线段OA上，且OM=2MA，N为BC的中点，‎ 所以=．‎ 所以=．‎ 故选B．‎ ‎　‎ ‎3．执行如图所示的程序框图．若n=5，则输出s的值是（　　）‎ A．﹣21 B．11 C．43 D．86‎ ‎【考点】程序框图．‎ ‎【分析】框图首先先输入n，给s赋值1，给i赋值1，然后判断判断框中的条件是否满足，满足则执行s=s+（﹣2）i，i=i+1，不满足则跳出循环输出s的值．‎ ‎【解答】解：框图首先输入n=5，给s赋值1，给i赋值1．‎ 判断1≤5成立，执行s=1+（﹣2）1=﹣1，i=1+1=2；‎ 判断2≤5成立，执行s=﹣1+（﹣2）2=3，i=2+1=3；‎ 判断3≤5成立，执行s=3+（﹣2）3=﹣5，i=3+1=4；‎ 判断4≤5成立，执行s=﹣5+（﹣2）4=11，i=4+1=5；‎ 判断5≤5成立，执行s=11+（﹣2）5=﹣21，i=5+1=6；‎ 判断6≤5不成立，跳出循环，输出s的值为﹣21．‎ 故答案为：A．‎ ‎　‎ ‎4．双曲线x2﹣my2=1的实轴长是虚轴长的2倍，则m等于（　　）‎ A． B． C．2 D．4‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】利用双曲线的标准方程即可得出a与b的关系，即可得到m的值．‎ ‎【解答】解：双曲线x2﹣my2=1化为，∴a2=1，，‎ ‎∵实轴长是虚轴长的2倍，∴2a=2×2b，化为a2=4b2，，解得m=4．‎ 故选D．‎ ‎　‎ ‎5．已知命题p：“∀x∈R时，都有”； 命题q：“∃x°∈R，使sinx°+cosx°=2时”，则下列判断正确的是（　　）‎ A．p∨q为假命题 B．p∧q为真命题 C．￢p∧q为真命题 D．￢p∨￢q为假命题 ‎【考点】复合命题的真假．‎ ‎【分析】命题p：取x=时，x2﹣x+=0，即可判断出p命题的真假． 命题q：由sinx+cosx=≤，即可判断出真假．‎ ‎【解答】解：命题p：取x=时，x2﹣x+=0，因此p是假命题：‎ 命题q：∵sinx+cosx=≤，因此q是假命题．‎ ‎∴p∨q是假命题．‎ 故选：A．‎ ‎　‎ ‎6．已知m，n表示两条不同直线，α表示平面，下列说法正确的是（　　）‎ A．若m∥α，n∥α，则m∥n B．若m⊥α，n⊂α，则m⊥n C．若m⊥α，m⊥n，则n∥α D．若m∥α，m⊥n，则n⊥α ‎【考点】空间中直线与直线之间的位置关系．‎ ‎【分析】A．运用线面平行的性质，结合线线的位置关系，即可判断；‎ B．运用线面垂直的性质，即可判断；‎ C．运用线面垂直的性质，结合线线垂直和线面平行的位置即可判断；‎ D．运用线面平行的性质和线面垂直的判定，即可判断．‎ ‎【解答】解：A．若m∥α，n∥α，则m，n相交或平行或异面，故A错；‎ B．若m⊥α，n⊂α，则m⊥n，故B正确；‎ C．若m⊥α，m⊥n，则n∥α或n⊂α，故C错；‎ D．若m∥α，m⊥n，则n∥α或n⊂α或n⊥α，故D错．‎ 故选B．‎ ‎　‎ ‎7．若实数a，b满足a2+b2≤1，则关于x的方程x2﹣2x+a+b=0有实数根的概率是（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】由题意，以a为横坐标、b为纵坐标建立直角坐标系，可得满足a2+b2≤1的点（a，b）在单位圆及其内部，如图所示．若关于x的方程x2﹣2x+a+b=0有实数根，则点（a，b）满足a+b≤1，即在单位圆内且直线a+b=1的下方．由此结合几何概型计算公式，用图中黄色阴影部分的面积除以单位圆的面积，即可得到所求的概率．‎ ‎【解答】解：∵实数a，b满足a2+b2≤1，‎ ‎∴以a为横坐标、b为纵坐标建立直角坐标系，‎ 可得所有的点（a，b）在以O为圆心，半径为1的圆及其内部，‎ 即单位圆及其内部，如图所示 若关于x的方程x2﹣2x+a+b=0有实数根，‎ 则满足△=4﹣4（a+b）≥0，解之得a+b≤1‎ 符合上式的点（a，b）在圆内且在直线a+b=1的下方，‎ 其面积为S1=π×12+×1×1=，‎ 又∵单位圆的面积为S=π×12=π ‎∴关于x的方程x2﹣2x+a+b=0无实数根的概率为P===‎ 故选：C ‎　‎ ‎8．设n=4sinxdx，则（x+）（x﹣）n的展开式中各项系数和为（　　）‎ A．1 B．2 C．3 D．4‎ ‎【考点】二项式系数的性质．‎ ‎【分析】利用微积分基本定理可得：n=4，令x=1，可得（x+）的展开式中各项系数和．‎ ‎【解答】解：n=4sinxdx==4，‎ 令x=1，可得（x+）的展开式中各项系数和=3×（﹣1）4=3．‎ 故选：C．‎ ‎　‎ ‎9．在三棱锥P﹣ABC中，△ABC为等边三角形，PA⊥平面ABC，且PA=AB，则二面角A﹣PB﹣C的平面角的正切值为（　　）‎ A． B． C． D．‎ ‎【考点】二面角的平面角及求法．‎ ‎【分析】取AB的中点为D，连结CD，过D作DE⊥PB，交PB于E，连CE，∠CED为二面角A﹣PB﹣C的平面角，由此能求出二面角A﹣PB﹣C的平面角的正切值．‎ ‎【解答】解：由题意知，取AB的中点为D，连结CD，‎ 过D作DE⊥PB，交PB于E，连CE，‎ ‎△ABC为等边三角形，‎ 故CD⊥AB，又PA⊥面ABC，‎ 所以CD⊥PA，‎ CD⊥平面PAB，‎ 而DE⊥PB，由三垂线定理，得CE⊥PB，‎ 所以∠CED为二面角A﹣PB﹣C的平面角，‎ 设AB=2，则CD=，‎ ‎∵△PAB是等腰直角三角形，且DE是斜边上中线的一半，‎ ‎∴DE=，‎ ‎∴tan∠CED===．‎ 故选：A．‎ ‎　‎ ‎10．若函数f（x）=x2+ax+在（，+∞）上是增函数，则a的取值范围是（　　）‎ A．[﹣1，0] B．[﹣1，+∞） C．[0，3] D．[3，+∞）‎ ‎【考点】利用导数研究函数的单调性；二次函数的性质．‎ ‎【分析】求出函数f（x）的导函数，由导函数在（，+∞）大于等于0恒成立解答案 ‎【解答】解：由f（x）=x2+ax+，得f′（x）=2x+a﹣=，‎ 令g（x）=2x3+ax2﹣1，‎ 要使函数f（x）=x2+ax+在（，+∞）是增函数，‎ 则g（x）=2x3+ax2﹣1在x∈（，+∞）大于等于0恒成立，‎ g′（x）=6x2+2ax=2x（3x+a），‎ 当a=0时，g′（x）≥0，g（x）在R上为增函数，则有g（）≥0，解得+﹣1≥0，a≥3（舍）；‎ 当a＞0时，g（x）在（0，+∞）上为增函数，则g（）≥0，解得+﹣1≥0，a≥3；‎ 当a＜0时，同理分析可知，满足函数f（x）=x2+ax+在（，+∞）是增函数的a的取值范围是a≥3（舍）．‎ 故选：D．‎ ‎　‎ ‎11．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（　　）‎ A．6 B．6 C．4 D．4‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】画出图形，结合三视图的数据求出棱长，推出结果即可．‎ ‎【解答】解：几何体的直观图如图：AB=4，BD=4，C到BD的中点的距离为：4，‎ ‎∴．AC==6，AD=4，‎ 显然AC最长．长为6．‎ 故选：B．‎ ‎　‎ ‎12．设F1、F2分别为双曲线：﹣=1（a＞0，b＞0）的左、右焦点，P为双曲线右支上任一点，若的最小值为8a，则该双曲线的离心率的取值范围是（　　）‎ A．[3，+∞） B．（1，3] C．（1，] D．[，+∞）‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】设|PF2|=t，则|PF1|=2a+t，故 ==4a++t≥8a，由2a≥c﹣a 及 e＞1 求得e 的范围．‎ ‎【解答】解：由双曲线的定义可得|PF1|﹣|PF2|=2a． 设|PF2|=t，则|PF1|=2a+t，‎ 故 ==4a++t≥4a+2=8a，当且仅当 t=2a时，等号成立．‎ 又∵t≥c﹣a，∴2a≥c﹣a，∴e=≤3．‎ 又因为 e＞1，故e 的范围为 （1，3]，‎ 故选B．‎ ‎　‎ 二、填空题（本大题共4小题，每小题5分，满分20分）.‎ ‎13．（x3+）7的展开式中的x5的系数是　35　（用数字填写答案）‎ ‎【考点】二项式定理的应用．‎ ‎【分析】根据所给的二项式，利用二项展开式的通项公式写出第r+1项，整理成最简形式，令x的指数为5求得r，再代入系数求出结果．‎ ‎【解答】解：根据所给的二项式写出展开式的通项，‎ Tr+1==；‎ 要求展开式中含x5的项的系数，‎ ‎∴21﹣4r=5，‎ ‎∴r=4，可得： =35．‎ 故答案为：35．‎ ‎　‎ ‎14．若命题“∀x∈R，ax2+2x+1＞0”为真命题，则a的取值范围为　（1，+∞）　．‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】若∀x∈R，ax2+2x+1＞0，则对应的二次函数y=ax2+2x+1的图象恒在x轴上方，即开口朝上且与x轴无交点，由此结合二次函数的图象和性质构造关于a的不等式，解不等式可得答案．‎ ‎【解答】解：∵p（x）：ax2+2x+1＞0，若对∀x∈R，p（x）是真命题，‎ ‎①当a=0时，2x+1＞0不恒成立．‎ ‎②当a≠0时，解得a＞1，故实数a的取值范围为（1，+∞），‎ 故答案为：（1，+∞）‎ ‎　‎ ‎15．过点（﹣4，0）作直线L与圆x2+y2+2x﹣4y﹣20=0交于A、B两点，如果|AB|=8，则L的方程为　x=﹣4或5x+12y+20=0　．‎ ‎【考点】直线与圆相交的性质．‎ ‎【分析】先求出圆心和半径，由弦长公式求出圆心到直线的距离为d的值，检验直线ι的斜率不存在时，满足条件；‎ 当直线ι的斜率存在时，设出直线ι的方程，由圆心到直线的距离等于3解方程求得斜率k，进而得到直线ι的方程．‎ ‎【解答】解：圆x2+y2+2x﹣4y﹣20=0 即 （x+1）2+（y﹣2）2=25，‎ ‎∴圆心（﹣1，2），半径等于5，设圆心到直线的距离为d，‎ 由弦长公式得8=2∴d=3． 当直线L的斜率不存在时，方程为x=﹣4，满足条件．‎ 当直线L的斜率存在时，设斜率等于 k，直线L的方程为y﹣0=k（x+4），即kx﹣y+4k=0，‎ 由圆心到直线的距离等于3得 =3，‎ ‎∴k=﹣，直线L的方程为5x+12y+20=0．‎ 综上，满足条件的直线L的方程为 x=﹣4或5x+12y+20=0，‎ 故答案为：x=﹣4或5x+12y+20=0．‎ ‎　‎ ‎16．如图，把椭圆的长轴AB分成8等份，过每个分点作x轴的垂线交椭圆的上半部分于P1，P2，P3，P4，P5，P6，P7七个点，F是椭圆的一个焦点则|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=　35　．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】利用椭圆的定义可求得|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=×2a，结合椭圆的标准方程即可求得答案．‎ ‎【解答】解：∵椭圆的方程为+=1，‎ ‎∴a=5，b=4，c=3．‎ ‎∵F是椭圆的一个焦点，设F′为椭圆的另一焦点，‎ 依题意|P1F|=|P7F′|，|P2F|=|P6F′|，|P3F|=|P4F′|，‎ ‎∴|P1F|+|P7F|=|P2F|+|P6F|=|P3F|+|P4F|=2a=10，‎ ‎∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=×2a=7a=35．‎ 故答案为：35．‎ ‎　‎ 三、解答题（本大题共6小题，满分70分）‎ ‎17．已知p：2x2﹣3x﹣2≥0，q：x2﹣（2a﹣2）x+a（a﹣2）≥0，若p是q的充分不必要条件．求实数a的取值范围．‎ ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】根据一元二次不等式的解法分别求出命题p和q，由p是q的充分不必要条件，可知p⇒q，从而求出a的范围：‎ ‎【解答】解：∵p：2x2﹣3x﹣2≥0，∴p：x≤﹣或x≥2，‎ q：x2﹣（2a﹣2）x+a（a﹣2）≥0，即（x﹣a）（x﹣（a﹣2））≥0，解得x≤a﹣2或x≥a，‎ p是q的充分不必要条件，∴p⇒q，且q推不出p，‎ ‎∴解得≤a≤2‎ 所以实数a的取值范围是：[，1]．‎ ‎　‎ ‎18．某同学在篮球场上进行投篮训练，先投“2分的篮”2次，每次投中的概率为，每投中一次得2分，不中得0分；再投“3分的篮”1次，每次投中的概率为，投中得3分，不中得0分，该同学每次投篮的结果相互独立，假设该同学要完成以上三次投篮．‎ ‎（1）求该同学恰好有2次投中的概率；‎ ‎（2）求该同学所得分X的分布列．‎ ‎【考点】离散型随机变量及其分布列；互斥事件的概率加法公式；相互独立事件的概率乘法公式．‎ ‎【分析】（1）确定共23=8，中情形，得出其中只有2次中的情形，（1，1，0），（1，0，1）（0，1，1）3种，根据概率公式求解即可．‎ ‎（2）根据题意得出随机变量的值：X得分共有6种情形，X=0，2，3，4，5，7，利用给出的数据得出相应的概率，列出分布列，求解数学期望即可．‎ ‎【解答】解：（1）总共有3次投篮，每次投不中记0，共23=8，中情形，其中只有2次中的情形，‎ ‎（1，1，0），（1，0，1）（0，1，1）3种，‎ 其发生的概率为P=×（1﹣）+×（1﹣）×+（1﹣）××=；‎ ‎（2）得分共有6种情形，X=0，2，3，4，5，7，‎ 得分X=0，的情形（0，0，0），P=××=，‎ 得分X=2，的情形（1，0，0），（0，1，0），P=2×××=，‎ 得分X=3，的情形（0，0，1），P=××=，‎ 得分X=4，的情形（1，1，0），P=××=，‎ 得分X=5，的情形（1，0，1），（0，1，1），P=2×××=，‎ 得分X=7，的情形（1，1，1），P=××=，‎ ‎∴X的分布列为：‎ ‎ X ‎ 0‎ ‎ 2‎ ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ 7‎ ‎ P ‎　‎ ‎19．如图，直三棱柱ABC﹣A1B1C1中，△ABC是等边三角形，D是BC的中点．‎ ‎（1）求证：A1B∥平面ADC1；‎ ‎（2）若AB=BB1，求A1D与平面ADC1所成角的正弦值．‎ ‎【考点】直线与平面所成的角；直线与平面平行的判定．‎ ‎【分析】（1）连接A1C交AC1于E，利用直三棱柱的性质、矩形的性质、三角形中位线的性质定理即可得到ED∥A1B，再利用线面平行的判定定理即可证明；‎ ‎（2）建立如图所示空间坐标系D﹣xyz．利用直线的方向向量和平面的法向量的夹角即可得出线面角．‎ ‎【解答】（1）证明：∵三棱柱ABC﹣A1B1C1是直三棱柱，∴四边形A1ACC1是矩形．‎ 连接A1C交AC1于E，则E是A1C的中点，‎ 又D是BC的中点，在△A1BC中，ED∥A1B．‎ ‎∵A1B⊄平面ADC1，ED⊂平面ADC1，∴A1B∥平面ADC1．‎ ‎（2）解：∵△ABC是等边三角形，D是BC的中点，∴AD⊥BC．‎ 以D为原点，建立如图所示空间坐标系D﹣xyz．‎ 令AB=BB1=2，得：D（0，0，0），A（，0，0），‎ A1（，0，2），C1（0，﹣1，2）．‎ 则=（，0，0），=（0，﹣1，2），‎ 设平面ADC1的法向量为=（x，y，z），‎ 得到，令z=1，则x=0，y=2，‎ ‎∴=（0，2，1）‎ 又=（，0，2），‎ ‎∴cos＜，＞==，‎ 所以A1D与平面ADC1所成角的正弦值为．‎ ‎　‎ ‎20．某校举行运动会，其中三级跳远的成绩在8.0米 （四舍五入，精确到0.1米） 以上的进入决赛，把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．‎ ‎（1）求进入决赛的人数；‎ ‎（2）经过多次测试后发现，甲成绩均匀分布在8～10米之间，乙成绩均匀分布在9.5～10.5米之间，现甲，乙各跳一次，求甲比乙远的概率．‎ ‎【考点】几何概型；频率分布直方图；古典概型及其概率计算公式．‎ ‎【分析】（1）由频率分直方图求出第6小组的频率，从而求出总人数，进而得到第4、5、6组成绩均进入决赛，由此能求出进入决赛的人数．‎ ‎（2）设甲、乙各跳一次的成绩分别为x、y米，则基本事件满足的区域为：，由此利用几何概型能求出甲比乙远的概率．‎ ‎【解答】解：（1）第6小组的频率为1﹣（0.04+0.10+0.14+0.28+0.30）=0.14，‎ ‎∴总人数为=50（人）．…‎ ‎∴第4、5、6组成绩均进入决赛，人数为（0.28+0.30+0.14）×50=36（人）‎ 即进入决赛的人数为36．…‎ ‎（2）设甲、乙各跳一次的成绩分别为x、y米，则基本事件满足的区域为，‎ 事件A“甲比乙远的概率”满足的区域为x＞y，如图所示．…‎ ‎∴由几何概型P（A）==．即甲比乙远的概率为．…‎ ‎　‎ ‎21．已知抛物线C：y2=2px（p＞0）的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有|FA|=|FD|．当点A的横坐标为3时，△ADF为正三角形．‎ ‎（1）求C的方程；‎ ‎（2）若直线l1∥l，且l1和C有且只有一个公共点E，证明直线AE过定点，并求出定点坐标．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】（1）根据抛物线的焦半径公式，结合等边三角形的性质，求出的p值；‎ ‎（2）设出点A的坐标，求出直线AB的方程，利用直线l1∥l，且l1和C有且只有一个公共点E，求出点E的坐标，写出直线AE的方程，将方程化为点斜式，可求出定点．‎ ‎【解答】解：（1）由题意知F（，0），设D（t，0）（t＞0），则FD的中点为（，0），‎ 因为|FA|=|FD|，由抛物线的定义知：3+=|t﹣|，解得t=3+p或t=﹣3（舍去）．‎ 由=3，解得p=2．所以抛物线C的方程为C的方程为y2=4x．‎ ‎（2）由（1）知F（1，0），‎ 设A（x1，y1），|FD|=|AF|=x1+1，‎ ‎∴D（x1+2，0），故直线AB的斜率为﹣，‎ 因为直线l1和直线AB平行，设直线l1的方程为y=﹣x+b，‎ 代入抛物线方程得y2+y﹣=0，‎ 由题意△=0，得b=﹣．‎ 设E（x2，y2），则x2=，y2=﹣．‎ 当y12≠4时，kAE=，‎ 可得直线AE的方程为y﹣y1=（x﹣x1），‎ 由y12=4x1，整理可得y=（x﹣1），直线AE恒过点F（1，0），‎ 当y12=4时，直线AE的方程为x=1，过点F（1，0），所以直线AE过定点F（1，0）．‎ ‎　‎ ‎22．设函数f（x）=﹣k（+lnx）（k为常数，e=2.71828…是自然对数的底数）．‎ ‎（Ⅰ）当k≤0时，求函数f（x）的单调区间；‎ ‎（Ⅱ）若函数f（x）在（0，2）内存在两个极值点，求k的取值范围．‎ ‎【考点】利用导数研究函数的单调性；函数在某点取得极值的条件．‎ ‎【分析】（Ⅰ）求出导函数，根据导函数的正负性，求出函数的单调区间；‎ ‎（Ⅱ）函数f（x）在（0，2）内存在两个极值点，等价于它的导函数f′（x）在（0，2）内有两个不同的零点．‎ ‎【解答】解：（Ⅰ）f（x）的定义域为（0，+∞），‎ ‎∴f′（x）=﹣k（﹣）‎ ‎=（x＞0），‎ 当k≤0时，kx≤0，‎ ‎∴ex﹣kx＞0，‎ 令f′（x）=0，则x=2，‎ ‎∴当0＜x＜2时，f′（x）＜0，f（x）单调递减；‎ 当x＞2时，f′（x）＞0，f（x）单调递增，‎ ‎∴f（x）的单调递减区间为（0，2），单调递增区间为（2，+∞）．‎ ‎（Ⅱ）由（Ⅰ）知，k≤0时，函数f（x）在（0，2）内单调递减，‎ 故f（x）在（0，2）内不存在极值点；‎ 当k＞0时，设函数g（x）=ex﹣kx，x∈（0，+∞）．‎ ‎∵g′（x）=ex﹣k=ex﹣elnk，‎ 当0＜k≤1时，‎ 当x∈（0，2）时，g′（x）=ex﹣k＞0，y=g（x）单调递增，‎ 故f（x）在（0，2）内不存在两个极值点；‎ 当k＞1时，‎ 得x∈（0，lnk）时，g′（x）＜0，函数y=g（x）单调递减，‎ x∈（lnk，+∞）时，g′（x）＞0，函数y=g（x）单调递增，‎ ‎∴函数y=g（x）的最小值为g（lnk）=k（1﹣lnk）‎ 函数f（x）在（0，2）内存在两个极值点 当且仅当 解得：e 综上所述，‎ 函数f（x）在（0，2）内存在两个极值点时，k的取值范围为（e，）‎