江苏省徐州市睢宁县古邳中学2019-2020学年高一下学期期中考试数学试卷 8页

数学 ‎ 一、选择题（每小题5分，合计50分）‎ ‎1．若直线过点(,－3)和点(,－4),则该直线的方程为（ ） ‎ ‎ A．y＝x－4 B. y＝x＋4 C . y＝x－6 D. y＝x＋2‎ ‎ 2. 不等式的解集为（ ）‎ A. B. C. D. ‎ ‎3．如果A(3, 1)、B(－2, k)、C(8, 11)在同一直线上，那么k的值是（ ）‎ ‎ A. －6 B. －7 C. －8 D. －9 ‎ ‎4．下列四个命题中错误的是(　 　) ‎ A．若直线，b互相平行，则直线，b确定一个平面 B．若四点不共面，则这四点中任意三点都不共线 C．若两条直线没有公共点，则这两条直线是异面直线 D．两条异面直线不可能垂直于同一个平面 ‎5. 在△ABC中，＝12，b＝13，C＝60°，此三角形的解的情况是（ ）‎ A．无解 B．一解 C． 二解 D．不能确定 ‎ ‎6．设m，n是不同的直线，α、β、γ是不同的平面，有以下四个命题：‎ ‎①⇒β∥γ；②⇒m⊥β；③⇒α⊥β；④⇒m∥α.其中正确的命题是(　 　)‎ A．①④ B．②③‎ C．①③ D．②④‎ ‎7. 在△ABC中，若，则△ABC的形状是（ ）‎ A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等腰或直角三角形 ‎ ‎8．如图，在正方体ABCD－A1B1C1D1中，E是AD的中点，则异面直线C1E与BC所成的角的 余弦值是(　　)‎ A. B. C. D. ‎ ‎9．已知b>>0且＋b=1，则有 （ ）‎ ‎ A． B． ‎ ‎ C． D． 2＋b2＞b＞＞＞2b ‎ ‎10．三棱柱的侧棱垂直于底面，且，，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为（ ）‎ A． B． C． D．‎ 二、填空题（每小题5分，合计30分）.‎ ‎11．不等式的解集为___▲____. ‎ ‎12．若圆锥的母线长是5，高是 4，则该圆锥的体积是__▲____.‎ ‎13．过点，在轴上和轴上的截距分别是且满足的直线方程为 ___▲____. ‎ ‎14. 若钝角三角形三边长分别是，则三角形的周长为__▲___.‎ ‎15．已知直线:,则恒过定点___▲____. ‎ ‎16. 在中，若，则的最小值为_ ▲ _.‎ 三、解答题（10分+12分+12分+12分+12分+12分=70分）‎ ‎17．(5分+5分)在直三棱柱中, , 为棱上任一点.‎ ‎(1)求证：直线∥平面；‎ ‎(2)求证：平面⊥平面.‎ ‎18. 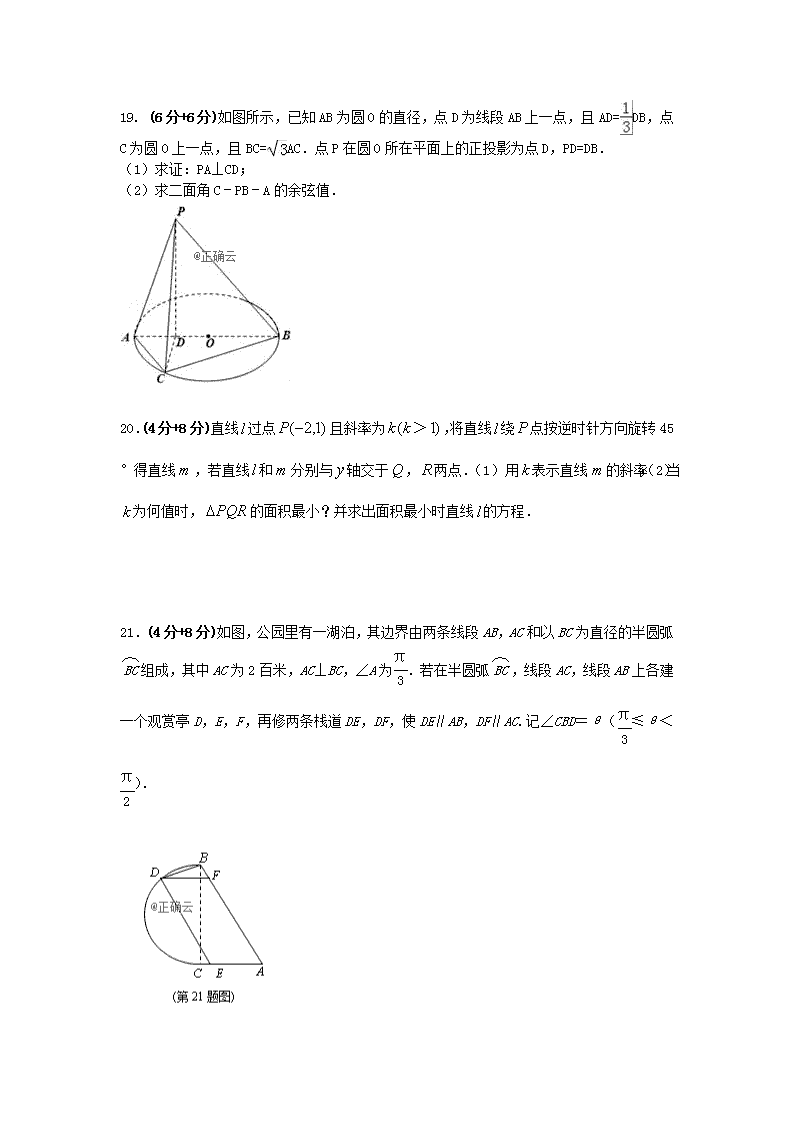(4分+8分)在锐角中，已知.‎ ‎(1) 求的值； (2) 若，，求的值.‎ ‎19. (6分+6分)如图所示，已知AB为圆O的直径，点D为线段AB上一点，且AD=DB，点C为圆O上一点，且BC=AC．点P在圆O所在平面上的正投影为点D，PD=DB．‎ ‎（1）求证：PA⊥CD；‎ ‎（2）求二面角C﹣PB﹣A的余弦值．‎ ‎20．(4分+8分)直线过点且斜率为＞，将直线绕点按逆时针方向旋转45°得直线，若直线和分别与轴交于，两点．（1）用表示直线的斜率；（2）当为何值时，的面积最小？并求出面积最小时直线的方程．‎ ‎21．(4分+8分)如图，公园里有一湖泊，其边界由两条线段AB，AC和以BC为直径的半圆弧组成，其中AC为2百米，AC⊥BC，∠A为．若在半圆弧，线段AC，线段AB上各建一个观赏亭D，E，F，再修两条栈道DE，DF，使DE∥AB，DF∥AC.记∠CBD＝θ（≤θ＜）．‎ ‎（1）试用θ表示BD的长；‎ ‎（2）试确定点E的位置，使两条栈道长度之和最大.‎ ‎22. (6分+6分)已知函数,‎ ‎（1）若存在，使得不等式有解，求实数的 取值范围；‎ ‎（2）若函数满足，若对任意且，不等式 恒成立，求实数m的最大值．‎ ‎ 高一数学期中试卷答案2019.4‎ 一选择题:‎ A C D C B C D A B C ‎ 二、填空题:‎ ‎11. 12. 13. 或； 14. 9 ‎ ‎15. 16. ‎ 三、解答题:‎ ‎17. (1)证明:由直三棱柱,得………………………………2分 ‎ ………………………5分 ‎(2)因为三棱柱为直三棱柱,所以,又,‎ 而,,且,‎ 所以……………8分 又,所以平面⊥平面…………………………………10分 ‎18. 解：（1）因为锐角△ABC中，，所以 又A＋B＋C＝p， 所以. ……….4分 ‎ ‎（2），，即，‎ ‎ ……….6分 将，，代入余弦定理：得： ‎ ‎， ……….11分 即. ………..12分 ‎19. 解析：（1）连接OC，由AD=BD知，点D为AO的中点，‎ 又∵AB为圆的直径，∴AC⊥BC，‎ ‎∵AC=BC，∴∠CAB=60°，‎ ‎∴△ACO为等边三角形，∴CD⊥AO． ……….2分 ‎∵点P在圆O所在平面上的正投影为点D，‎ ‎∴PD⊥平面ABC，又CD⊂平面ABC，‎ ‎∴PD⊥CD，PD∩AO=D，‎ ‎∴CD⊥平面PAB，PA⊂平面PAB，‎ ‎∴PA⊥CD． ……….6分 ‎（2）过点D作DE⊥PB，垂足为E，连接CE，‎ 由（1）知CD⊥平面PAB，又PB⊂平面PAB，‎ ‎∴CD⊥PB，又DE∩CD=D，‎ ‎∴PB⊥平面CDE，又CE⊂平面CDE，‎ ‎∴CE⊥PB，‎ ‎∴∠DEC为二面角C﹣PB﹣A的平面角．……….9分 设AB=4,则由（1）可知CD=，PD=BD=3，‎ ‎∴PB=3，则DE==，‎ ‎∴在Rt△CDE中，tan∠DEC==，‎ ‎∴cos∠DEC=，即二面角C﹣PB﹣A的余弦值为．……….12分 ‎20. 解：(1)设直线的倾斜角为，则直线的倾斜角为，‎ ‎ ………4分 ‎(2)直线的方程为，直线的方程为 令，得，∴‎ ‎ ……….6分 ‎∵，∴ ≥‎ ‎ ………9分 由得舍去，∴当时，的面积最小，最小值为，此时直线的方程是．………12分 ‎21. 解：（1）连结DC．在△ABC中，AC为2百米，AC⊥BC，∠A为，‎ 所以∠CBA＝，AB＝4，BC＝2．因为BC为直径，所以∠BDC＝，‎ 所以BD＝BCcosθ＝2cosθ． ……….4分 ‎（2）在△BDF中，∠DBF＝θ＋，∠BFD＝，BD＝2cosθ，‎ 所以＝＝，‎ 所以DF＝4cosθsin(＋θ)，且BF＝4cosθ，所以DE＝AF=4－4cosθ，‎ ‎ ……….6分 ‎ 所以DE＋DF＝4－4cosθ＋4cosθsin(＋θ)=sin2θ－cos2θ＋3‎ ‎ ＝2 sin(2θ－)＋3． ………8分 ‎ ‎ 因为≤θ＜，所以≤2θ－＜，‎ 所以当2θ－＝，即θ＝时，DE＋DF有最大值5，此时E与C重合．………11分 答：当E与C重合时，两条栈道长度之和最大……….12分 ‎22. 解：（1）．‎ 对任意，有：‎ ‎．‎ 因为，所以，所以，‎ 因此在R上递增．………………………………………2分 令,则且 ‎，所以，‎ 即在时有解．‎ 当时，，所以．…………………………6分 ‎(2)因为，所以()， ………7分 所以．‎ 不等式恒成立，‎ 即，‎ ‎， ………………10分 因为，由基本不等式可得：，当且仅当时，等号成立．‎ 所以，则实数m的最大值为．…………………………12分