数学卷·2018届江西省宜春市上高二中高二上学期第三次月考数学试卷（理科）+（解析版） 25页

‎2016-2017学年江西省宜春市上高二中高二（上）第三次月考数学试卷（理科）‎ ‎　‎ 一、选择题（每小题5分，共60分）‎ ‎1．已知a∥α，b⊂α，则直线a与直线b的位置关系是（　　）‎ A．平行 B．平行或异面 C．相交或异面 D．异面 ‎2．“a+b=﹣2”是“直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切”的（　　）‎ A．既不充分也不必要条件 B．必要不充分条件 C．充要条件 D．充分不必要条件 ‎3．已知命题p：∃c＞0，方程x2﹣x+c=0 有解，则￢p为（　　）‎ A．∀c＞0，方程x2﹣x+c=0无解 B．∀c≤0，方程x2﹣x+c=0有解 C．∃c＞0，方程x2﹣x+c=0无解 D．∃c＜0，方程x2﹣x+c=0有解 ‎4．一个圆锥的表面积为6π（单位：m2），且它的侧面展开图是一个半圆，则圆锥的底面半径为（　　）（单位：m）‎ A． B． C．1 D．2‎ ‎5．已知抛物线C：x2=2py（p＞0）的焦点为F，直线x=4与x轴的交点为P，与C的交点为Q，且，则抛物线C的方程为（　　）‎ A．x2=2y B．x2=4y C．x2=8y D．x2=16y ‎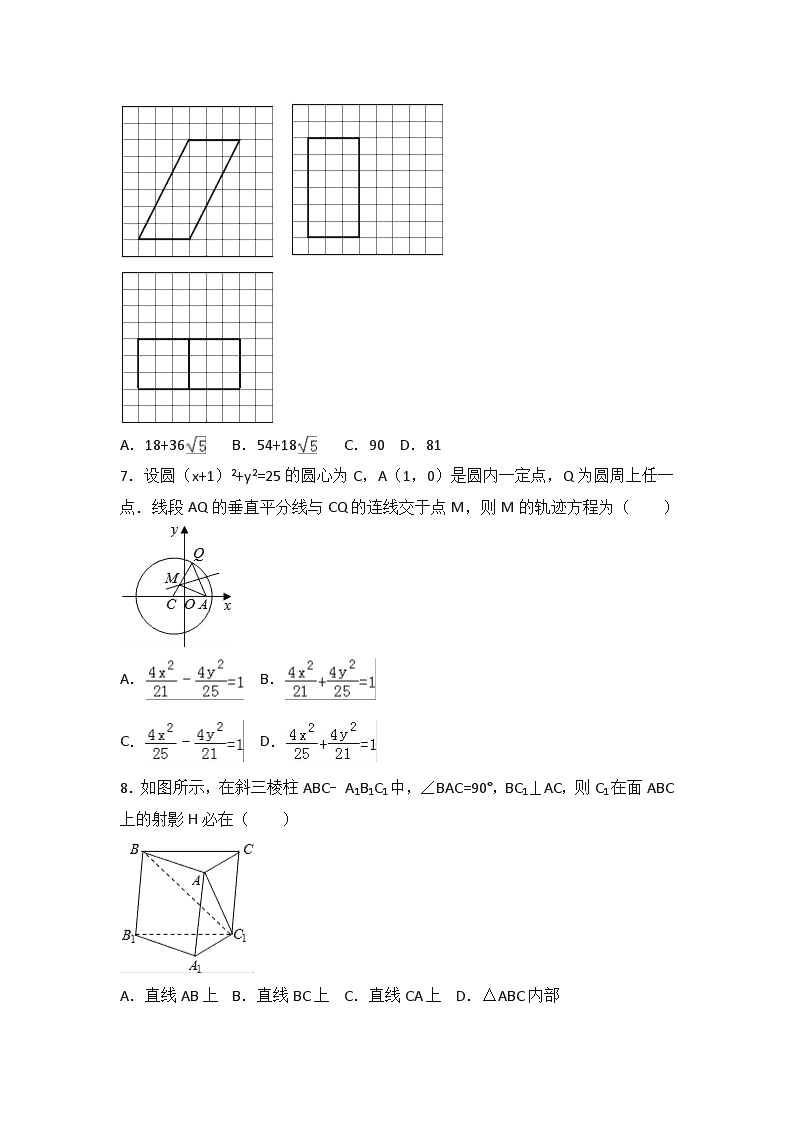6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（　　）‎ A．18+36 B．54+18 C．90 D．81‎ ‎7．设圆（x+1）2+y2=25的圆心为C，A（1，0）是圆内一定点，Q为圆周上任一点．线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为（　　）‎ A． B．‎ C． D．‎ ‎8．如图所示，在斜三棱柱ABC﹣A1B1C1中，∠BAC=90°，BC1⊥AC，则C1在面ABC上的射影H必在（　　）‎ A．直线AB上 B．直线BC上 C．直线CA上 D．△ABC内部 ‎9．已知O为坐标原点，F是椭圆C： +=1（a＞b＞0）的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（　　）‎ A． B． C． D．‎ ‎10．已知四面体P﹣ABC中，PA=4，AC=2，PB=BC=2，PA⊥平面PBC，则四面体P﹣ABC的内切球半径与外接球半径的比（　　）‎ A． B． C． D．‎ ‎11．定义：平面内横坐标为整数的点称为“左整点”，过函数图象上任意两个“左整点”作直线，则倾斜角大于45°的直线条数为（　　）‎ A．10 B．11 C．12 D．13‎ ‎12．若椭圆+=1（a＞b＞0）和圆x2+y2=（+c）2，（c为椭圆的半焦距），有四个不同的交点，则椭圆的离心率e的取值范围是（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（每小题5分，共20分）‎ ‎13．在正四棱锥P﹣ABCD中，PA=2，直线PA与平面ABCD所成角为60°，E为PC的中点，则异面直线PA与BE所成角的大小为　　．‎ ‎14．已知方程+=﹣1表示椭圆，求k的取值范围．　　．‎ ‎15．已知条件p：≤﹣1，条件q：x2+x＜a2﹣a，且￢q的一个充分不必要条件是￢p，求实数a的取值范围．‎ ‎16．已知实数p＞0，直线4x+3y﹣2p=0与抛物线y2=2px和圆（x﹣）2+y2=从上到下的交点依次为A，B，C，D，则的值为　　．‎ ‎　‎ 三、解答题（共70分）‎ ‎17．已知p：“∃x0∈R，使得x02+mx0+2m﹣3＜0”；q：命题“∀x∈[1，2]，x2﹣m≤0”，若p∨q为真，p∧q为假，求实数m的取值范围．‎ ‎18．如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AD=CD=AB=2，点E为AC中点．将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D﹣ABC，如图2所示．‎ ‎（1）在CD上找一点F，使AD∥平面EFB；‎ ‎（2）求点C到平面ABD的距离．‎ ‎19．已知圆C：x2+y2﹣2x+4y﹣4=0，是否存在斜率为1的直线l，使l被圆C截得的弦长AB为直径的圆过原点，若存在求出直线的方程l，若不存在说明理由．‎ ‎20．如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是平行四边形，且AB=1，BC=2，∠ABC=60°，E为BC的中点，AA1⊥平面ABCD．‎ ‎（Ⅰ）证明：平面A1AE⊥平面A1DE；‎ ‎（Ⅱ）若DE=A1E，试求二面角E﹣A1C﹣D的余弦值．‎ ‎21．已知过点A（﹣4，0）的动直线l与抛物线C：x2=2py（p＞0）相交于B、C两点．当l的斜率是时，．‎ ‎（1）求抛物线C的方程；‎ ‎（2）设BC的中垂线在y轴上的截距为b，求b的取值范围．‎ ‎22．已知椭圆C：的离心率为，点在椭圆C上．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）设动直线l与椭圆C有且仅有一个公共点，判断是否存在以原点O为圆心的圆，满足此圆与l相交两点P1，P2（两点均不在坐标轴上），且使得直线OP1，OP2的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由．‎ ‎　‎ ‎2016-2017学年江西省宜春市上高二中高二（上）第三次月考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（每小题5分，共60分）‎ ‎1．已知a∥α，b⊂α，则直线a与直线b的位置关系是（　　）‎ A．平行 B．平行或异面 C．相交或异面 D．异面 ‎【考点】空间中直线与直线之间的位置关系；空间中直线与平面之间的位置关系．‎ ‎【分析】直接利用直线与平面平行的性质定理以及定义，推出结果即可．‎ ‎【解答】解：∵a∥α，∴a与α没有公共点，b⊂α，∴a、b没有公共点，‎ ‎∴a、b平行或异面．‎ 故选：B．‎ ‎　‎ ‎2．“a+b=﹣2”是“直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切”的（　　）‎ A．既不充分也不必要条件 B．必要不充分条件 C．充要条件 D．充分不必要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】利用点到直线的距离公式与直线与圆相切的性质可得： =，即可判断出结论．‎ ‎【解答】解：∵直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切，∴=，解得a+b=±2．‎ ‎∴“a+b=﹣2”是“直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切”的充分不必要条件．‎ 故选：D．‎ ‎　‎ ‎3．已知命题p：∃c＞0，方程x2﹣x+c=0 有解，则￢p为（　　）‎ A．∀c＞0，方程x2﹣x+c=0无解 B．∀c≤0，方程x2﹣x+c=0有解 C．∃c＞0，方程x2﹣x+c=0无解 D．∃c＜0，方程x2﹣x+c=0有解 ‎【考点】命题的否定．‎ ‎【分析】直接利用特称命题的否定是全称命题写出结果即可．‎ ‎【解答】解：因为特称命题的否定是全称命题，所以，命题p：∃c＞0，方程x2﹣x+c=0 有解，则￢p为∀c＞0，方程x2﹣x+c=0无解．‎ 故选：A．‎ ‎　‎ ‎4．一个圆锥的表面积为6π（单位：m2），且它的侧面展开图是一个半圆，则圆锥的底面半径为（　　）（单位：m）‎ A． B． C．1 D．2‎ ‎【考点】旋转体（圆柱、圆锥、圆台）．‎ ‎【分析】设出圆锥的底面半径，由它的侧面展开图是一个半圆，分析出母线与半径的关系，结合圆锥的表面积为3π，构造方程，可求出圆锥的底面半径．‎ ‎【解答】解：设圆锥的底面的半径为r，圆锥的母线为l，‎ 则由πl=2πr得l=2r，‎ 而S=πr2+πr•2r=3πr2=6π 故r2=2‎ 解得r=．‎ 故选B．‎ ‎　‎ ‎5．已知抛物线C：x2=2py（p＞0）的焦点为F，直线x=4与x轴的交点为P，与C的交点为Q，且，则抛物线C的方程为（　　）‎ A．x2=2y B．x2=4y C．x2=8y D．x2=16y ‎【考点】抛物线的简单性质．‎ ‎【分析】设Q（4，y0），代入x2=2py，得，从而求出|PQ|，|QF|，由此求出P，从而能求出抛物线C的方程．‎ ‎【解答】解：设Q（4，y0），代入x2=2py，得，‎ ‎∴|PQ|=，|QF|=，‎ 由题设得，‎ 解得p=﹣2（舍去）或p=2，‎ ‎∴C的方程为x2=4y．‎ 故选：B．‎ ‎　‎ ‎6．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（　　）‎ A．18+36 B．54+18 C．90 D．81‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】由已知中的三视图可得：该几何体是一个以俯视图为底面的斜四棱柱，进而得到答案．‎ ‎【解答】解：由已知中的三视图可得：该几何体是一个以俯视图为底面的斜四棱柱，‎ 其底面面积为：3×6=18，‎ 前后侧面的面积为：3×6×2=36，‎ 左右侧面的面积为：3××2=18，‎ 故棱柱的表面积为：18+36+9=54+18．‎ 故选：B．‎ ‎　‎ ‎7．设圆（x+1）2+y2=25的圆心为C，A（1，0）是圆内一定点，Q为圆周上任一点．线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为（　　）‎ A． B．‎ C． D．‎ ‎【考点】圆锥曲线的轨迹问题．‎ ‎【分析】根据线段中垂线的性质可得，|MA|=|MQ|，又|MQ|+|MC|=半径5，故有|MC|+|MA|=5＞|AC|，根据椭圆的定义判断轨迹椭圆，求出a、b值，即得椭圆的标准方程．‎ ‎【解答】解：由圆的方程可知，圆心C（﹣1，0），半径等于5，设点M的坐标为（x，y ），∵AQ的垂直平分线交CQ于M，‎ ‎∴|MA|=|MQ|． 又|MQ|+|MC|=半径5，∴|MC|+|MA|=5＞|AC|．依据椭圆的定义可得，‎ 点M的轨迹是以 A、C 为焦点的椭圆，且 2a=5，c=1，∴b=，‎ 故椭圆方程为 =1，即 ．‎ 故选D．‎ ‎　‎ ‎8．如图所示，在斜三棱柱ABC﹣A1B1C1中，∠BAC=90°，BC1⊥AC，则C1在面ABC上的射影H必在（　　）‎ A．直线AB上 B．直线BC上 C．直线CA上 D．△ABC内部 ‎【考点】平面与平面垂直的判定；棱柱的结构特征．‎ ‎【分析】如图，C1在面ABC上的射影H必在两个相互垂直平面的交线上，所以证明面ABC⊥面ABC1就可以了．‎ ‎【解答】解： ⇒CA⊥面ABC1‎ ‎⇒面ABC⊥面ABC1，‎ ‎∴过C1在面ABC内作垂直于平面ABC，‎ 垂线在面ABC1内，也在面ABC内，‎ ‎∴点H在两面的交线上，即H∈AB．‎ 故选A ‎　‎ ‎9．已知O为坐标原点，F是椭圆C： +=1（a＞b＞‎ ‎0）的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（　　）‎ A． B． C． D．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】由题意可得F，A，B的坐标，设出直线AE的方程为y=k（x+a），分别令x=﹣c，x=0，可得M，E的坐标，再由中点坐标公式可得H的坐标，运用三点共线的条件：斜率相等，结合离心率公式，即可得到所求值．‎ ‎【解答】解：由题意可设F（﹣c，0），A（﹣a，0），B（a，0），‎ 令x=﹣c，代入椭圆方程可得y=±b=±，‎ 可得P（﹣c，±），‎ 设直线AE的方程为y=k（x+a），‎ 令x=﹣c，可得M（﹣c，k（a﹣c）），令x=0，可得E（0，ka），‎ 设OE的中点为H，可得H（0，），‎ 由B，H，M三点共线，可得kBH=kBM，‎ 即为=，‎ 化简可得=，即为a=3c，‎ 可得e==．‎ 故选：A．‎ ‎　‎ ‎10．已知四面体P﹣ABC中，PA=4，AC=2，PB=BC=2，PA⊥平面PBC，则四面体P﹣ABC的内切球半径与外接球半径的比（　　）‎ A． B． C． D．‎ ‎【考点】直线与平面垂直的判定．‎ ‎【分析】确定△PBC为等边三角形，△‎ ABC为等腰三角形，分别求出四面体P﹣ABC的内切球半径与外接球半径，即可得出结论．‎ ‎【解答】解：由题意，已知PA⊥面PBC，PA=4，PB=BC=2，AC=2，‎ 所以，由勾股定理得到：AB=2，PC=2，‎ 所以，△PBC为等边三角形，△ABC为等腰三角形，‎ 等边三角形PBC所在的小圆的直径PD==4，‎ 那么，四面体P﹣ABC的外接球直径2R==4，所以，R=2，‎ VP﹣ABC=S△PBC•PA=••12•4=4，‎ 表面积S=•2•4•2+•12+•2•5=16，‎ 设内切球半径为r，那么4=•16r，所以r=，‎ 所以四面体P﹣ABC的内切球半径与外接球半径的比=．‎ 故选：A．‎ ‎　‎ ‎11．定义：平面内横坐标为整数的点称为“左整点”，过函数图象上任意两个“左整点”作直线，则倾斜角大于45°的直线条数为（　　）‎ A．10 B．11 C．12 D．13‎ ‎【考点】直线的倾斜角．‎ ‎【分析】由题意求出函数的图象上“左整点”的个数，然后求出任意两个“左整点”作直线，则倾斜角大于45°的直线条数．‎ ‎【解答】解：函数 “左整点”，共有7个，如图 所以任意两个“左整点”作直线，则倾斜角大于45°的直线，‎ 过（3，0）点有5条，（2，）点有3条，过（1，2）1条，过（﹣3，0）有2条，共计11条．‎ 故选B．‎ ‎　‎ ‎12．若椭圆+=1（a＞b＞0）和圆x2+y2=（+c）2，（c为椭圆的半焦距），有四个不同的交点，则椭圆的离心率e的取值范围是（　　）‎ A． B． C． D．‎ ‎【考点】圆与圆锥曲线的综合．‎ ‎【分析】由题设知，由，得2c＞b，再平方，4c2＞b2，；由，得b+2c＜2a，．综上所述，．‎ ‎【解答】解：∵椭圆和圆为椭圆的半焦距）的中心都在原点，‎ 且它们有四个交点，‎ ‎∴圆的半径，‎ 由，得2c＞b，再平方，4c2＞b2，‎ 在椭圆中，a2=b2+c2＜5c2，‎ ‎∴；‎ 由，得b+2c＜2a，‎ 再平方，b2+4c2+4bc＜4a2，‎ ‎∴3c2+4bc＜3a2，‎ ‎∴4bc＜3b2，‎ ‎∴4c＜3b，‎ ‎∴16c2＜9b2，‎ ‎∴16c2＜9a2﹣9c2，‎ ‎∴9a2＞25c2，‎ ‎∴，‎ ‎∴．‎ 综上所述，．‎ 故选A．‎ ‎　‎ 二、填空题（每小题5分，共20分）‎ ‎13．在正四棱锥P﹣ABCD中，PA=2，直线PA与平面ABCD所成角为60°，E为PC的中点，则异面直线PA与BE所成角的大小为　45°　．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】连接AC，BD交于点O，连接OE，OP，先证明∠PAO即为PA与面ABCD所成的角，即可得出结论．‎ ‎【解答】解：连接AC，BD交于点O，连接OE，OP 因为E为PC中点，所以OE∥PA，‎ 所以∠OEB即为异面直线PA与BE所成的角．‎ 因为四棱锥P﹣ABCD为正四棱锥，‎ 所以PO⊥平面ABCD，‎ 所以AO为PA在面ABCD内的射影，所以∠‎ PAO即为PA与面ABCD所成的角，即∠PAO=60°，‎ 因为PA=2，所以OA=OB=1，OE=1．‎ ‎△PBC中，PB=PC=2，BC=，∴2（4+2）=4+4BE2，∴BE=，‎ ‎∴OE2+OB2=BE2，‎ 所以在直角三角形EOB中∠OEB=45°，即面直线PA与BE所成的角为45°．‎ 故答案为为45°．‎ ‎　‎ ‎14．已知方程+=﹣1表示椭圆，求k的取值范围．　（﹣∞，﹣3）　．‎ ‎【考点】椭圆的标准方程．‎ ‎【分析】化曲线方程为椭圆的标准方程，由分母大于0且不相等求得k的取值范围．‎ ‎【解答】解：由+=﹣1，得，‎ ‎∵方程+=﹣1表示椭圆，‎ ‎∴，解得k＜﹣3．‎ ‎∴k的取值范围是（﹣∞，﹣3）．‎ 故答案为：（﹣∞，﹣3）．‎ ‎　‎ ‎15．已知条件p：≤﹣1，条件q：x2+x＜a2﹣a，且￢q的一个充分不必要条件是￢p，求实数a的取值范围．‎ ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】先化简p，q，根据￢q的一个充分不必要条件是￢p等价于p是q的一个必要不充分条件，分类讨论即可求出a的取值范围．‎ ‎【解答】解：由≤﹣1，得p：﹣3≤x＜1，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 由x2+x＜a2﹣a得（x+a）[x﹣（a﹣1）]＜0，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 当a=时，q：∅；‎ 当a＜时，q：（a﹣1，﹣a）；‎ 当a＞时，q：（﹣a，a﹣1）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 由题意得，p是q的一个必要不充分条件，‎ 当a=时，满足条件；‎ 当a＜时，（a﹣1，﹣a）⊆[﹣3，1]得a∈[﹣1，），‎ 当a＞时，（﹣a，a﹣1）⊆[﹣3，1]得a∈（，2]，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 综上，a∈[﹣1，2]﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎　‎ ‎16．已知实数p＞0，直线4x+3y﹣2p=0与抛物线y2=2px和圆（x﹣）2+y2=从上到下的交点依次为A，B，C，D，则的值为　　．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】设A（x1，y1），D（x2，y2），抛物线的焦点为F，由题得|BF|=|CF|=．由抛物线的定义得：|AC|=|AF|+|CF|=+x1+=x1+p，同理得|BD|=x2+p．联立直线4x+3y﹣2p=0与抛物线y2=2px且消去x解出y1=，y2=﹣2p，所以x1=，x2=2p，进而得到答案．‎ ‎【解答】解：设A（x1，y1），D（x2，y2），抛物线的焦点为F，‎ 由题意得|BF|=|CF|=，‎ 由抛物线的定义得：|AC|=|AF|+|CF|=+x1+=x1+p，同理得|BD|=x2+p．‎ 联立直线4x+3y﹣2p=0与抛物线y2=2px且消去x得：2y2+3py﹣2p2=0‎ 解得：y1=，y2=﹣2p，所以x1=，x2=2p 所以==．‎ 故答案为．‎ ‎　‎ 三、解答题（共70分）‎ ‎17．已知p：“∃x0∈R，使得x02+mx0+2m﹣3＜0”；q：命题“∀x∈[1，2]，x2﹣m≤0”，若p∨q为真，p∧q为假，求实数m的取值范围．‎ ‎【考点】复合命题的真假．‎ ‎【分析】求出命题p，q为真命题的等价条件，结合p∨q为真，p∧q为假得到p，q一真一假，根据条件关系解不等式即可．‎ ‎【解答】解：∵命题p为真命题的充要条件是△＞0，即m2﹣4（2m﹣3）＞0，‎ ‎∴m＞6或m＜2．…‎ 命题q为真命题的充要条件是m≥4 …‎ 若p∨q为真，p∧q为假，则p，q一真一假 若p真q假，得m＜2；‎ 若q真p假得4≤m≤6‎ ‎∴实数m的取值范围为m＜2或4≤m≤6 …‎ ‎　‎ ‎18．如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AD=CD=AB=2，点E为AC中点．将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D﹣ABC，如图2所示．‎ ‎（1）在CD上找一点F，使AD∥平面EFB；‎ ‎（2）求点C到平面ABD的距离．‎ ‎【考点】点、线、面间的距离计算；直线与平面平行的判定．‎ ‎【分析】（1）取CD的中点F，连结EF，BF，在△ACD中，可证AD∥EF，又EF⊆平面EFB AD⊄平面EFB，可证AD∥平面EFB．‎ ‎（2）设点C到平面ABD的距离为h，由于可证AD⊥BD，可得，又三棱锥B﹣ACD的高BC=2，S△ACD=2，由=即可解得点C到平面ABD的距离．‎ ‎【解答】（1）取CD的中点F，连结EF，BF，‎ 在△ACD中，∵E，F分别为AC，DC的中点，‎ ‎∴EF为△ACD的中位线 ‎∴AD∥EF，‎ EF⊆平面EFB，AD⊄平面EFB ‎∴AD∥平面EFB．‎ ‎（2）设点C到平面ABD的距离为h，‎ ‎∵平面ADC⊥平面ABC，且BC⊥AC，‎ ‎∴BC⊥平面ADC，‎ ‎∴BC⊥AD，而AD⊥DC•‎ ‎∴AD⊥平面BCD，即AD⊥BD•‎ ‎∴•‎ ‎∴三棱锥B﹣ACD的高BC=2，S△ACD=2，‎ ‎∴=‎ ‎∴可解得：h=．‎ ‎　‎ ‎19．已知圆C：x2+y2﹣2x+4y﹣4=0，是否存在斜率为1的直线l，使l被圆C截得的弦长AB为直径的圆过原点，若存在求出直线的方程l，若不存在说明理由．‎ ‎【考点】直线与圆相交的性质．‎ ‎【分析】将圆C化成标准方程，假设存在以AB为直径的圆M，圆心M的坐标为（a，b）．因为CM⊥l，则有kCM•kl=﹣1，表示出直线l的方程，从而求得圆心到直线的距离，再由：求解．‎ ‎【解答】解：圆C化成标准方程为（x﹣1）2+（y+2）2=9，假设存在以AB为直径的圆M，圆心M的坐标为（a，b）．‎ ‎∵CM⊥l，即kCM•kl=×1=﹣1‎ ‎∴b=﹣a﹣1‎ ‎∴直线l的方程为y﹣b=x﹣a，即x﹣y﹣2a﹣1=0‎ ‎∴|CM|2=（）2=2（1﹣a）2‎ ‎∴|MB|2=|CB|2﹣|CM|2=﹣2a2+4a+7‎ ‎∵|MB|=|OM|‎ ‎∴﹣2a2+4a+7=a2+b2，得a=﹣1或，‎ 当a=时，b=﹣，此时直线l的方程为x﹣y﹣4=0‎ 当a=﹣1时，b=0，此时直线l的方程为x﹣y+1=0‎ 故这样的直线l是存在的，方程为x﹣y﹣4=0或x﹣y+1=0．‎ ‎　‎ ‎20．如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是平行四边形，且AB=1，BC=2，∠ABC=60°，E为BC的中点，AA1⊥平面ABCD．‎ ‎（Ⅰ）证明：平面A1AE⊥平面A1DE；‎ ‎（Ⅱ）若DE=A1E，试求二面角E﹣A1C﹣D的余弦值．‎ ‎【考点】二面角的平面角及求法；平面与平面垂直的判定．‎ ‎【分析】（Ⅰ）依题意推导出△ABE是正三角形，DE⊥AE，DE⊥AA1，从而DE⊥平面A1AE，由此能证明平面A1AE⊥平面A1DE．‎ ‎（Ⅱ）以C为原点，CD，CA，CC1分别为x，y，z轴建立空间直角坐标系，利用向量法能求出二面角E﹣A1C﹣D的余弦值．‎ ‎【解答】证明：（Ⅰ）依题意，‎ ‎∴△ABE是正三角形，∠AEB=60°，‎ ‎∵，‎ ‎∴∠AED=180°﹣∠CED﹣∠AEB=90°，∴DE⊥AE，‎ ‎∵AA1⊥平面ABCD，DE⊆平面ABCD，‎ ‎∴DE⊥AA1，∵AA1∩AE=A，∴DE⊥平面A1AE，‎ ‎∵DE⊆平面A1DE，∴平面A1AE⊥平面A1DE． ‎ 解：（Ⅱ）连接AC，由题可知AC⊥CD，又DE=A1E，故 故以C为原点，CD，CA，CC1分别为x，y，z轴建立空间直角坐标系，则C（0，0，0），‎ D（1，0，0），E（﹣，，0），A1（0，），‎ 故=（﹣，，0），=（0，），=（1，0，0），‎ 设面EA1C的一个法向量=（x1，y1，z1），则，即，‎ 令，则=（），‎ 设平面DA1C的一个法向量=（a，b，c），‎ 则，取b=﹣，得=（0，﹣，），‎ 故cos＜＞==，‎ 由图可知二面角E﹣A1C﹣D为钝角，∴二面角E﹣A1C﹣D的余弦值为．‎ ‎　‎ ‎21．已知过点A（﹣4，0）的动直线l与抛物线C：x2=2py（p＞0）相交于B、C两点．当l的斜率是时，．‎ ‎（1）求抛物线C的方程；‎ ‎（2）设BC的中垂线在y轴上的截距为b，求b的取值范围．‎ ‎【考点】直线与圆锥曲线的综合问题．‎ ‎【分析】（1）设出B，C的坐标，利用点斜式求得直线l的方程，与抛物线方程联立消去x，利用韦达定理表示出x1+x2和x1x2，根据求得y2=4y1，最后联立方程求得y1，y2和p，则抛物线的方程可得．‎ ‎（2）设直线l的方程，AB中点坐标，把直线与抛物线方程联立，利用判别式求得k的范围，利用韦达定理表示出x1+x2，进而求得x0，利用直线方程求得y0，进而可表示出AB的中垂线的方程，求得其在y轴上的截距，根据k的范围确定b的范围．‎ ‎【解答】解：（1）设B（x1，y1），C（x2，y2），由已知k1=时，l方程为y=（x+4）即x=2y﹣4．‎ 由得2y2﹣（8+p）y+8=0‎ ‎①②∴‎ 又∵，∴y2=4y1③‎ 由①②③及p＞0得：y1=1，y2=4，p=2，即抛物线方程为：x2=4y．‎ ‎（2）设l：y=k（x+4），BC中点坐标为（x0，y0）‎ 由得：x2﹣4kx﹣16k=0④‎ ‎∴．‎ ‎∴BC的中垂线方程为 ‎∴BC的中垂线在y轴上的截距为：b=2k2+4k+2=2（k+1）2‎ 对于方程④由△=16k2+64k＞0得：k＞0或k＜﹣4．‎ ‎∴b∈（2，+∞）‎ ‎　‎ ‎22．已知椭圆C：的离心率为，点在椭圆C上．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）设动直线l与椭圆C有且仅有一个公共点，判断是否存在以原点O为圆心的圆，满足此圆与l相交两点P1，P2（两点均不在坐标轴上），且使得直线OP1，OP2的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由．‎ ‎【考点】圆锥曲线的定值问题；椭圆的标准方程．‎ ‎【分析】（Ⅰ）利用离心率列出方程，通过点在椭圆上列出方程，求出a，b然后求出椭圆的方程．‎ ‎（Ⅱ）当直线l的斜率不存在时，验证直线OP1，OP2的斜率之积．‎ 当直线l的斜率存在时，设l的方程为y=kx+m与椭圆联立，利用直线l与椭圆C有且只有一个公共点，推出m2=4k2+1，通过直线与圆的方程的方程组，设P1（x1，y1），P2（x2，y2），结合韦达定理，求解直线的斜率乘积，推出k1•k2为定值即可．‎ ‎【解答】（本小题满分14分）‎ ‎（Ⅰ）解：由题意，得，a2=b2+c2，…‎ 又因为点在椭圆C上，‎ 所以，…‎ 解得a=2，b=1，，‎ 所以椭圆C的方程为．…‎ ‎（Ⅱ）结论：存在符合条件的圆，且此圆的方程为x2+y2=5．…‎ 证明如下：‎ 假设存在符合条件的圆，并设此圆的方程为x2+y2=r2（r＞0）．‎ 当直线l的斜率存在时，设l的方程为y=kx+m．…‎ 由方程组得（4k2+1）x2+8kmx+4m2﹣4=0，…‎ 因为直线l与椭圆C有且仅有一个公共点，‎ 所以，即m2=4k2+1．…‎ 由方程组得（k2+1）x2+2kmx+m2﹣r2=0，…‎ 则．‎ 设P1（x1，y1），P2（x2，y2），则，，…‎ 设直线OP1，OP2的斜率分别为k1，k2，‎ 所以 ‎=，…‎ 将m2=4k2+1代入上式，得．‎ 要使得k1k2为定值，则，即r2=5，验证符合题意．‎ 所以当圆的方程为x2+y2=5时，圆与l的交点P1，P2满足k1k2为定值．…‎ 当直线l的斜率不存在时，由题意知l的方程为x=±2，‎ 此时，圆x2+y2=5与l的交点P1，P2也满足．‎ 综上，当圆的方程为x2+y2=5时，圆与l的交点P1，P2满足斜率之积k1k2为定值．…‎ ‎　‎