2013届高考数学一轮复习 指数函数 8页

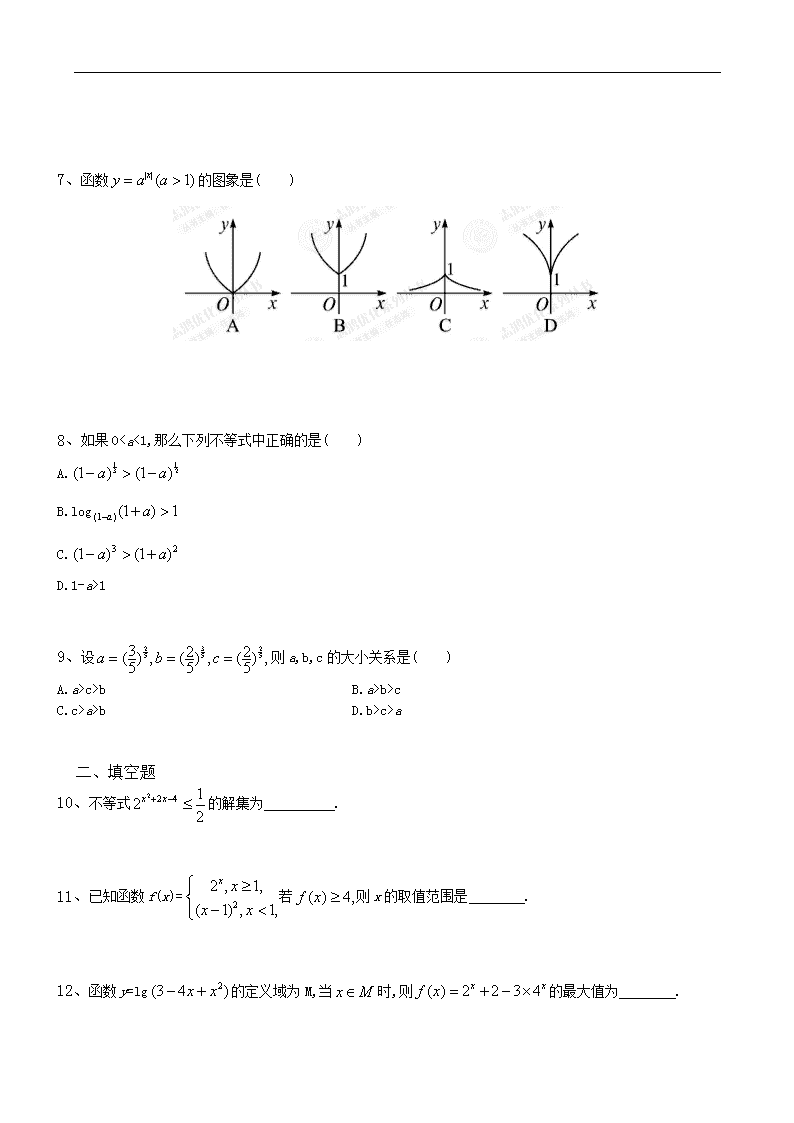
‎2013届高考一轮复习 指数函数 一、选择题 ‎1、与函数的图象关于直线y=x对称的曲线C对应的函数为g(x),则的值为( ) ‎ A. B.1 C. D.-1 ‎ ‎2、下列四类函数中,有性质”对任意的x>0,y>0,函数f(x)满足f(x+y)=f(x)f(y)”的是( ) ‎ A.幂函数 B.对数函数 ‎ C.指数函数 D.余弦函数 ‎ ‎3、(2011江西高考,理7)观察下列各式:125,15 625,78 125,…,则的末四位数字为( ) ‎ A.3125 B.5625 ‎ C.0625 D.8125 ‎ ‎4、已知正数x满足 则的最小值为( ) ‎ A.1 B. C. D. ‎ ‎5、若函数满足则f(x)的单调递减区间是( ) ‎ A.] B. [2,+ ‎ C. [-2,+ D.] ‎ ‎6、定义运算 则函数的图象是( ) ‎ ‎ ‎ ‎7、函数的图象是( ) ‎ ‎ ‎ ‎8、如果01 ‎ ‎9、设则a,b,c的大小关系是( ) ‎ A.a>c>b B.a>b>c ‎ C.c>a>b D.b>c>a ‎ 二、填空题 ‎10、不等式的解集为 . ‎ ‎11、已知函数f(x)=若则x的取值范围是 . ‎ ‎12、函数y=lg的定义域为M,当时,则的最大值为 . ‎ 三、解答题 ‎13、(2011上海高考,理20)已知函数,其中常数a,b满足. ‎ ‎(1)若ab>0,判断函数f(x)的单调性; ‎ ‎(2)若ab<0,求f(x+1)>f(x)时的x的取值范围.‎ ‎14、设函数f(x)=1-e. ‎ ‎(1)证明当x>-1时; ‎ ‎(2)设当时求a的取值范围. ‎  ‎ ‎15、计算:(1)(0.; ‎ ‎. ‎ 以下是答案 一、选择题 ‎1、 D ‎ 解析:依题意得g(x)=log ‎ 所以log. ‎ ‎2、 C ‎ 解析:本题考查幂的运算性质. ‎ ‎3、 D ‎ 解析:由观察易知的末四位数字为的末四位数字为的末四位数字为的末四位数字为的末四位数字为3125,故周期T=4.又由于2 011=因此的末四位数字是8125. ‎ ‎4、 C ‎ 解析:如图易得2x+y的最大值为4, ‎ ‎ ‎ 从而的最小值为选C. ‎ ‎5、 B ‎ 解析:由得于是因此f(x).因为g(x)=|2x-4|在[2,+上单调递增,所以f(x)的单调递减区间是[2,+.‎ ‎6、 A ‎ 解析:由题意,得 故选A. ‎ ‎7、B ‎ 解析:因为的图象是下凸的,过点(0,1),选B. ‎ ‎8、 A ‎ 解析:因为0.故选A. ‎ ‎9、 A ‎ 解析:∵在上是增函数,且 ‎ ‎∴即a>c. ‎ ‎∵在R上是减函数,且 ‎ ‎∴即b3或x<1, ‎ ‎∴M={x|x>3或x<1}. ‎ ‎. ‎ ‎∵x>3或x<1,∴或. ‎ ‎∴当即x=log时,f(x)最大,最大值为. ‎ 三、解答题 ‎13、 解:(1)当a>0,b>0时,因为、都随x的增大而增大,所以函数f(x)单调递增; ‎ 当a<0,b<0时,因为、都随x的增大而减小,所以函数f(x)单调递减.‎ ‎(2)f(x. ‎ ‎(ⅰ)当a<0,b>0时 ‎ 解得x>log; ‎ ‎(ⅱ)当a>0,b<0时 ‎ 解得x-1时当且仅当e.‎ 令g(x)=e则g′(x)=e. ‎ 当时,g′在上是增函数; ‎ 当x<0时,g′(x)<0,g(x)在上是减函数.‎ 于是g(x)在x=0处取到最小值,因而当R时,g(x)即e. ‎ 所以当x>-1时. ‎ ‎(2)由题设此时. ‎ 当a<0时,若则不成立; ‎ 当时,令h(x)=axf(x)+f(x)-x,则 ‎ 当且仅当 ‎ h′(x)=af(x)+axf′(x)+f′(x)-1 ‎ ‎=af(x)-axf(x)+ax-f(x). ‎ ‎(ⅰ)当时,由(1)知x), ‎ h′a(x+1)f(x)-f(x)=(2a ‎ h(x)在上是减函数即. ‎ ‎(ⅱ)当时,由(1)知 ‎ h′(x)=af(x)-axf(x)+ax-f(x) ‎ af(x)-f(x) ‎ ‎=(2a-1-ax)f(x), ‎ 当时,h′(x)>0, ‎ 所以h(x)>h(0)=0,即 ‎ 综上,a的取值范围是. ‎15、 解:(1)原式. ‎ ‎(2)原式. ‎