数学文卷·2018届广东省深圳市高三第一次调研考试（2018 12页

绝密★启用前 深圳市2018届高三年级第一次调研考试 ‎ 数学（文科） 2018.3‎ 第I卷（选择题共60分）‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合A={xlx-2<0}，B={xlex>}，则AB=‎ A.（0，1] B.[-1，0) C.[-1，2) D.[0,2)‎ ‎2.已知aR，i为虚数单位，若复数纯虚数，则a=‎ A.0 B.1 C.2 D.1‎ ‎3.其食品研究部门为了解一种酒品的储藏年份与芳香度之间的相关关系，在市场上收集到了一部分不同年份的该酒品，并测定了其芳香度（如下表）。‎ 年份x ‎0‎ ‎1‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 芳香度y ‎1.3‎ ‎1.8‎ ‎5.6‎ ‎7.4‎ ‎9.3‎ 由最小二乘法得到回归方程=1.03x+1.13，但不小心在检测后滴到表格上一滴检测液，污损了一个数据，请你推断该数据为 A.6.1‎‎ B.6.28 C.6.5 D.6.8‎ ‎4.设有下面四个命题：‎ p1:，n2>2n；‎ p2：xR,“x>1”是“x>2”的充分不必要条件；‎ P3：命题“若x=y，则 sin x=siny”的逆否命题是“若sin xsiny，则xy”；‎ P4: 若“pVq”是真命题，则p一定是真命题。‎ 其中为真命题的是 A.p1,p2 B.p2,p3 C.p2，p4 D.p1,p3‎ ‎5.已知焦点在x轴上的双曲线的一条渐近线的倾斜角为，且其焦点到渐近线的距离为2，则该双曲线的标准方程为 A. B. c. D.‎ ‎6.两名同学分3本不同的书，其中一人没有分到书，另一人分得3本书的概率为 A. B. C. D.‎ ‎7.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等。意思是现有松树高5尺，竹子高2尺，松树每天长自 己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一般高?‎ 如图是源于其思想的一个程序框图，若输入的x=5，y=2，输出的n为4，则程序框图 中的 中应填入 A. B. C. 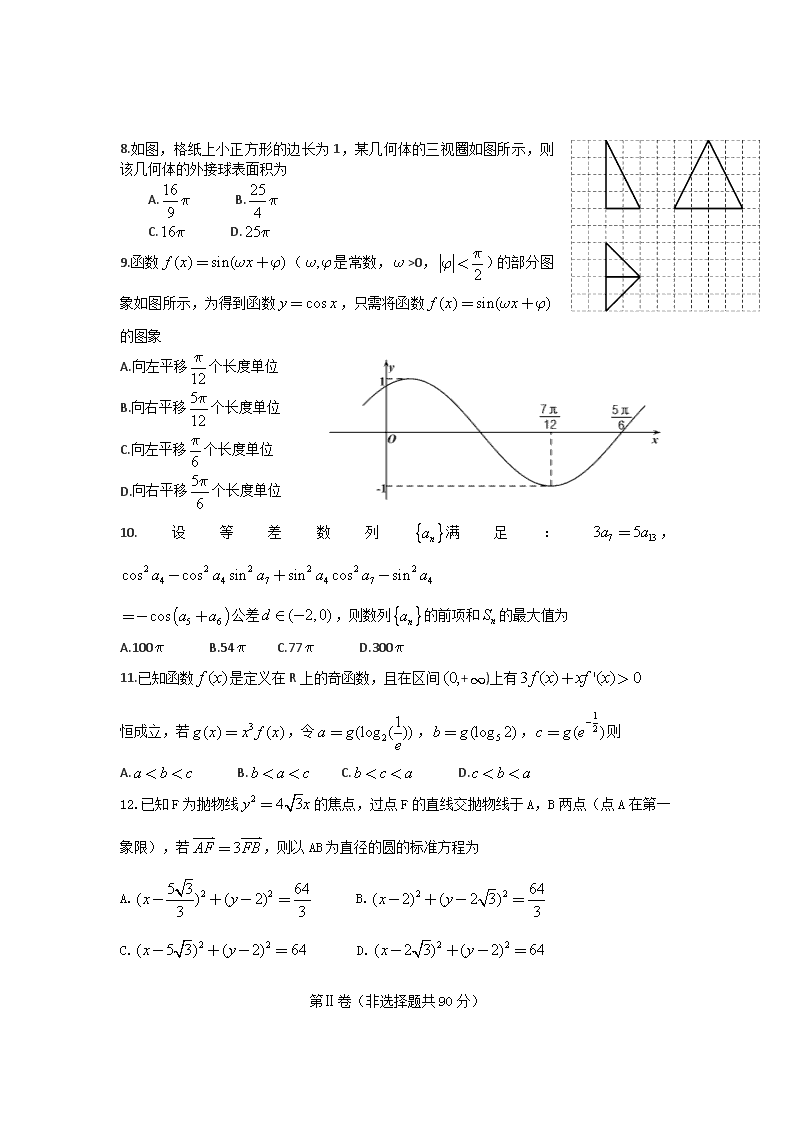D.‎ ‎8.如图，格纸上小正方形的边长为1，某几何体的三视圈如图所示，则该几何体的外接球表面积为 A. B. ‎ C. D.‎ ‎9.函数（是常数，>0，）的部分图象如图所示，为得到函数，只需将函数的图象 A.向左平移个长度单位 B.向右平移个长度单位 C.向左平移个长度单位 D.向右平移个长度单位 ‎10.设等差数列满足：，‎ 公差，则数列的前项和的最大值为 A.100 B.54 C.77 D.300‎ ‎11.已知函数是定义在R上的奇函数，且在区间+)上有 恒成立，若，令，，则 A. B. C. D.‎ ‎12.已知F为抛物线的焦点，过点F的直线交抛物线于A，B两点（点A在第一象限），若，则以AB为直径的圆的标准方程为 A. B.‎ C. D.‎ ‎ 第Ⅱ卷（非选择题共90分）‎ ‎ 本卷包括必考题和选考题两部分。第13~21题为必考题，每道试题考生都必须作 答，第22~23题为选考题，考生根据要求作答。 二、填空题：本题共4小题，每小题5分，共20分。 13.已知向量，.若向量平行，则m= . 14.若实数x，y满足约束条件，则的最小值为 . 15.曲线y=ex-1+x的一条切线经过坐标原点，则该切线方程为 .‎ 16. 如图，在△ABC中，∠ABC=90°，AC=2CB=，P是△ABC内一动点，∠BPC= 120°，则AP的最小值为 .‎ 三、解答题：本题共6小题，共70分。请将解答过程书写在答题纸上，并写出文字说明、证明过程或演算步骤. 17.（本小题满分12分） 设数列的前n项和为，,（nN). （I）求数列的通项公式； （Ⅱ）设，求数列的前n项和 ‎18.（本小题满分12分） 如图，在三棱柱ABC-A1B1C1中，底面ABC为等边三角形，平面BCC1B1平面 ABB1A1，且∠B1BA=45°. （I）证明：ACAA1； （Ⅱ）若AA1=AB=2，求三棱柱ABC-A1B1C1的体积。 19.（本小题满分12分） 某重点中学将全部高一新生分成A，B两个成绩相当（成绩的均值、方差都相同）的级部，A级部采用传统形式的教学方式，B级部采用新型的基于信息化的自主学习教学方式. 期末考试后分别从两个级部中各随机抽取100名学生的数学成绩进行统计，得到如下数据： ‎ A部 成绩分组 ‎[90,100)‎ ‎[100,110)‎ ‎[110,120)‎ ‎[120,130)‎ ‎[130,140)‎ ‎[140,150]‎ 频数 ‎18‎ ‎23‎ ‎29‎ ‎23‎ ‎6‎ ‎1‎ ‎ ‎ B部 成绩分组 ‎[90,100)‎ ‎[100,110)‎ ‎[110,120)‎ ‎[120,130)‎ ‎[130,140)‎ ‎[140,150]‎ 频数 ‎8‎ ‎16‎ ‎24‎ ‎28‎ ‎21‎ ‎3‎ 若记成绩不低于130分者为“优秀”。 （I）根据上表数据分别估计A，B两个级部“优秀”的概率； ‎ ‎（Ⅱ)填写下面的列联表，并根据列联表判断是否有99%的把握认为“优秀”与教学方 式有关?‎ 级部 级部 是否优秀 优秀 不优秀 合计 A部 B部 合计 ‎（Ⅲ）根据上表数据完成下面的频率分布直方图，并根据频率分布直方图，分别求出 A,B两个级部的中位数的估计值（精确到0.01)；请根据以上计算结果初步分析A，B两 个级部的数学成绩的优劣.‎ ‎20.（本小题满分12分）‎ 已知椭圆C（a>b>0)的离心率为，直线：x+2y=4与椭圆有且只有一个交点T.‎ ‎（I）求椭圆C的方程和点T的坐标；‎ ‎（Ⅱ)O为坐标原点，与OT平行的直线与椭圆C交于不同的两点A，B，求△‎ ‎0AB的面积最大时直线的方程.‎ ‎21.（本小题满分12分）‎ 已知函数.‎ ‎（I）讨论函数的单调性；‎ ‎（Ⅱ）当时，关于的不等式在[0，+)上恒成立，求的取值 范围.‎ 请考生在第22、23题中任选一道作答，如果多做，则按所做的第1题计分。作签时。 请用2B铅笔在答题卡上将所选题目题号后的方框涂黑。 22.（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系xOy中，直线/的参数方程为为参数）.在以O为极点、 x轴的正半轴为极轴的极坐标系中，曲线C的方程为 （I）求直线的普通方程和曲线C的直角坐标方程； （Ⅱ)已知点P(a,1)，设直线与曲线C的两个交点为A，B，若.求 的值。 23.（本小题满分10分）选修4-5：不等式选讲 已知且. （I）若是恒成立，求x的取值范围； （Ⅱ）证明：≥4. ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎