2018-2019学年江苏省泰州市姜堰区高二下学期期中考试数学（理）试题 Word版 10页

江苏省泰州市姜堰区2018～2019学年度第二学期期中调研试题 高 二 数 学（理）‎ ‎（考试时间：120分钟 总分160分）‎ 注意事项：所有试题的答案均填写在答题纸上，答案写在试卷上的无效．‎ 一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸相应的答题线上）‎ ‎1．从9道选择题与3道填空中任选一道进行解答，不同的选择方法有 ▲ ．‎ ‎2．某学校高三年级700人，高二年级700人，高一年级800人，若采用分层抽样的办法，从高一年级抽取80人，则全校总共抽取 ▲ 人.‎ ‎3．执行如图所示的伪代码，最后输出的值为 ▲ ．‎ ‎1000 1500 2000 2500 3000 3500 4000‎ ‎0.0005‎ ‎0.0004‎ ‎0.0003‎ ‎0.0002‎ ‎0.0001‎ 月收入(元)‎ 第4题 ‎ ‎ 第3题 ‎4．一个社会调查机构就某地居民的月收入情况调查了1000人，并根据所得数据绘制了样本频率分布直方图（如图所示），则月收入在[2000，3500）范围内的人数为 ▲ ． ‎ ‎5．已知某人连续5次投掷飞镖的环数分别是8，9，10，10，8，则该组数据的方差为 ▲ ．‎ 第7题 ‎6．有4种不同的蔬菜，从中选出3种，分别种植在不同土质的3块土地上进行实验，则不同的种植方法共 ▲ 种．（用数字作答）‎ ‎7.如图，圆和其内接正三角形，若在圆面上任意取一点，则 ‎ 点恰好落在三角形外的概率为 ▲ ．‎ ‎8.的展开式中的常数项为 ▲ .‎ 第11题 ‎9．袋中装有形状、大小都相同的 4只球，其中 1 只白球，1 只红球，2 只黄球从中一次随机摸出 2只球，则这 2只球颜色不同的概率为 ▲ ．‎ ‎10．若，‎ 第13题 则的值为 ▲　　．‎ 11． 一只电子蚂蚁在如图所示的网格线上由原点出发,沿向 上或向右方向爬至点,记可能的爬行方法总数为,‎ 则= ▲ ．‎ 12． 已知,,点M在直线OC上运动，则的最小值为 ▲ ．‎ 13． 在一个如图所示的6个区域栽种观赏植物，要求同一块区域中种同一种植物，相邻的两块区域中种不同的植物.现有4种不同的植物可供选择，则不同的栽种方案的总数为 ▲　　．‎ ‎14．对于各数不相等的正整数组（i1, i2, …, in），（n是不小于2的正整数），如果在p>q时有，则称ip和iq是该数组的一个“好序”，一个数组中“好序”的个数称为此数组的“好序数”，例如，数组（1, 3, 4, 2）中有好序“1, 3”，“1, 4”，“1, 2”，“3, 4”，其“好序数”等于4. 若各数互不相等的正整数组（a1, a2, a3, a4, a5, a6, a7）的“好序数”等于3，则（a7，a6, a5, a4, a3, a2, a1）的“好序数”是 ▲ .‎ 二、解答题：（本大题共6小题，共90分.解答应写出文字说明,证明过程或演算步骤）‎ ‎15．(本题满分14分) ‎ 从5本不同的科普书和4本不同的数学书中选出4本，送给4位同学，每人1本，问：‎ ‎（1）如果科普书和数学书各选2本，共有多少种不同的送法？（各问用数字作答）‎ ‎（2）如果科普书甲和数学书乙必须送出，共有多少种不同的送法？‎ ‎（3）如果选出的4本书中至少有3本科普书，共有多少种不同的送法？‎ ‎16．(本题满分14分)‎ 在班级活动中，4 名男生和3名女生站成一排表演节目：（写出必要的数学式，结果用数字作答）‎ ‎（1）三名女生互不相邻，有多少种不同的站法？ ‎ ‎（2）四名男生相邻有多少种不同的排法？ ‎ ‎（3）女生甲不能站在左端，女生乙不能站在右端，有多少种不同的排法？‎ ‎（4）甲乙丙三人按高低从左到右有多少种不同的排法？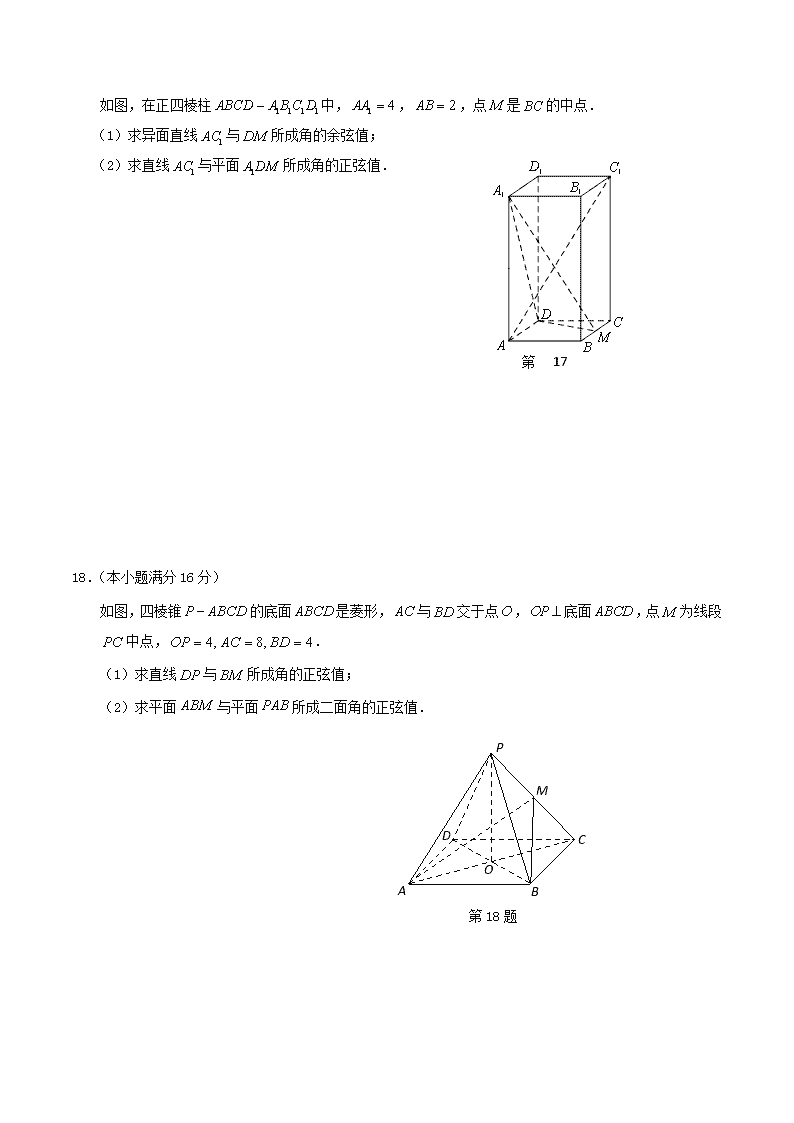（甲乙丙三位同学身高互不相等）‎ ‎17．(本题满分14分)‎ 如图，在正四棱柱中，，，点是的中点．‎ 第17题 ‎（1）求异面直线与所成角的余弦值；‎ ‎（2）求直线与平面所成角的正弦值．‎ ‎ ‎ ‎18．（本小题满分16分）‎ 如图，四棱锥的底面是菱形，与交于点，底面，点为线段中点，.‎ ‎（1）求直线与所成角的正弦值；‎ ‎（2）求平面与平面所成二面角的正弦值．‎ M A B C D O P 第18题 19． ‎(本题满分16分)‎ 已知.‎ ‎（1）若，求及的值；‎ ‎（2）若，求最大的系数；‎ ‎（3）定义，若化简.‎ ‎20．(本题满分16分)‎ 设，在集合的所有元素个数为2的子集中,把每个子集的较大元素相加和记为a，较小元素之和记为b.‎ ‎(1)当n=3时,求a, b的值；‎ ‎(2)当n=4时,求集合的所有3个元素子集中所有元素之和;‎ ‎(3)对任意的，是否为定值？若是定值，请给出证明并求出这个定值；若不是，请说明理由.‎ 姜堰区2018～2019学年度第二学期期中调研试题评分标准 高 二 数 学（理）‎ 一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸相应的答题线上）‎ ‎1. 12 2. 220 3. 14 4. 700 5. 6. 24 7. ‎ ‎8. 2 9. 10. 16 11. 21 12. 13. 588 14. 18‎ 二、解答题：（本大题共6小题，共90分.解答应写出文字说明,证明过程或演算步骤）‎ ‎15.（本小题14分）‎ 解：（1）从5本故事书中选2本有种选法，从4数学书中选2本有种选法，再把4本书给4位同学有种，‎ 所以科普书和数学书各选2本，共有种不同的送法.-- ----------4分 ‎（2）因为科普书甲和数学书乙必须送出，所以再从其余7本书选2本有种，再把4本书给4位同学有种，所以共有种不同的送法.--------------9分 ‎（3）选出4本故事书有种，选出3本故事书有种，再把4本书给4位同学有种，所以至少有3本科普书的送法为种.------------14分 ‎16.（本小题14分）‎ 解：（1）先排4个男生有种，再把3个女生插人两个男生之间或两端有种，所以三个女生互不相邻的排法为=1440---------------3分 ‎（2）4个男生作为一个整体与3个女生有种排法，男生之间有种排法，所以四名男生相邻有种排法-------------------------6分 ‎（3）法一、女生乙站在左端有种，女生乙不站在左端，且女生甲不能站在左端，女生乙不能站在右端有种，所以女生甲不能站在左端，女生乙不能站在右端，有种不同的排法.-------------------------10分 法二、7个人有种排法，女生甲在左端有种，女生乙在右端有种，女生甲在左端同时女生乙在右端有种，所以女生甲不能站在左端，女生乙不能站在右端，有种不同的排法.-------------------------10分 ‎（4）法一、7个人有种排法，甲乙丙三人有种，其中只有一种符合从高到低排列，所以甲乙丙三人按高低从左到右有种不同的排法.----------------------14分 法二、先从7个位置中选3个位置有种，甲乙丙三人去站，只有一种，其余4个人站4个位置有种，所以甲乙丙三人按高低从左到右有种不同的排法.---14分 17. ‎（本小题14分）‎ 解：在正四棱柱中，以为原点，、、分别为轴、轴、轴建立如图所示空间直角坐标系．‎ 因为，，，‎ 所以，， ‎ 所以，‎ 所以异面直线与所成角的余弦值为.-----------------------------5分 ‎(2)，设平面的一个法向量为．‎ 则，得，取，得，，‎ 故平面的一个法向量为．--------------------9分 ‎ 于是，--------12分 所以直线与平面所成角的正弦值为．--------------14分 17. ‎（本小题16分）‎ 解：（1）因为是菱形，所以．又底面，以为原点，直线 分别为轴，轴，轴，建立如图所示空间直角坐标系．‎ 则,,,,,．‎ M A B C D O P 第18题 x y z 所以，，，‎ ‎，．‎ 则………3分 故直线与所成角的余弦值为. ………5分 直线与所成角的正弦值为.…7分 ‎（2），．．‎ 设平面的一个法向量为，‎ 则，得，令，得，．‎ 得平面的一个法向量为．…………………9分 又,‎ 设平面的一个法向量为，‎ 得，令，得，．‎ 得平面的一个法向量为．……………11分 所以，，．‎ 则.…………13分 故平面与平面所成二面角的正弦值为. ………………16分 ‎19．(本题满分16分)‎ 解：（1）若，，‎ 令,则，------------------------------------1分 令，则 所以.-------------------------------------3分 ‎（2）若，其通项公式为，由不等式—------------------------5分 解得，且，∴.--------------------------------7分 所以.-------------------------------9分 ‎（3）若-----------------------10分 ‎,----------------12分 ‎----------------14分 ‎----------------16分 ‎20.（1）集合的所有2元子集为，，，‎ 较大元素分别为2，3，3，所以；‎ 较小元素分别为1，1，2，所以.---------------------------------------4分 ‎（2）含有元素1的子集有个，同理含有2,3,4的子集也有个，于是所求元素之和为;-------------------------------------8分 ‎(3)是为定值------------------9分 定值为------------------10分 法1：当n≥4，n∈N*，‎ ‎-----------------12分 ‎--------------14分 所以，.--------------16分 法2：集合时，在其2元子集中，含n的有n-1个；含n-1且n-1较大的有n-2个；······；含2且2较大的有1个，所以----8分 ‎，-------------------------------------------10分 集合时，在其2元子集中，含1的有n-1个；含2且2较小的有n-2个；······；含n-1且n-1较小的有1个，所以-----------------------13分 所以.--------------------------------------------------------------------16分