数学卷·2018届湖南省永州四中高二上学期期末数学试卷（理科）+（解析版） 30页

‎2016-2017学年湖南省永州四中高二（上）期末数学试卷（理科）‎ ‎　‎ 一.选择题（每题5分，共60分）‎ ‎1．已知a，b∈R，则命题“若a2+b2=0，则a=0或b=0”的否命题是（　　）‎ A．若a2+b2≠0，则a≠0且b≠0 B．若a2+b2≠0，则a≠0或b≠0‎ C．若a≠0且b≠0，则a2+b2≠0 D．若a≠0或b≠0，则a2+b2≠0‎ ‎2．双曲线=1的焦距为（　　）‎ A．2 B．4 C．2 D．4‎ ‎3．下列求导运算正确的是（　　）‎ A．（x）′=1 B．（x2cosx）′=﹣2xsinx C．（3x）′=3xlog3e D．（log2x）′=‎ ‎4．在复平面内，复数i（2﹣i）对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎5．若曲线处的切线与两坐标轴围成的三角形的面积为9，则a=（　　）‎ A．8 B．16 C．32 D．64‎ ‎6．某产品的广告费用x与销售额y的统计数据如下表 广告费用x（万元）‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y（万元）‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程=x+的为9.4，据此模型预报广告费用为6万元时销售额为（　　）‎ A．63.6万元 B．65.5万元 C．67.7万元 D．72.0万元 ‎7．某校在暑假组织社会实践活动，将8名高一年级学生，平均分配甲、乙两家公司，其中两名英语成绩优秀学生不能分给同一个公司；另三名电脑特长学生也不能分给同一个公司，则不同的分配方案有（　　）‎ A．36种 B．38种 C．108种 D．114种 ‎8．空间四边形ABCD中，AB=CD，边AB．CD所在直线所成的角为30°，E、F分别为边BC、AD的中点，则直线EF与AB所成的角为（　　）‎ A．75° B．15° C．75°或15° D．90°‎ ‎9．已知F1、F2分别是双曲线﹣=1（a＞0，b＞0）的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（　　）‎ A．（1，） B．（，+∞） C．（，2） D．（2，+∞）‎ ‎10．如果函数满足：对于任意的x1，x2∈[0，1]，都有|f（x1）﹣f（x2）|≤1恒成立，则a的取值范围是（　　）‎ A． B． C． D．‎ ‎11．如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1，CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（　　）‎ A． B． C． D．‎ ‎12．如图，正四面体ABCD的顶点C在平面α内，且直线BC与平面α所成角为45°，顶点B在平面α上的射影为点O，当顶点A与点O的距离最大时，直线CD与平面α所成角的正弦值等于（　　）‎ A． B． C． D．‎ ‎　‎ 二.填空题（每题5分，共20分）‎ ‎13．若命题“存在实数x，使x2+ax+1＜0”的否定是假命题，则实数a的取值范围为　　．‎ ‎14．已知抛物线Г：x2=2y，过点A（0，﹣2）和B（t，0）的直线与抛物线没有公共点，则实数t的取值范围是　　．‎ ‎15．如图，第一个图是正三角形，将此正三角形的每条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第2个图，将第2个图中的每一条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第3个图，如此重复操作至第n个图，用an表示第n个图形的边数，则数列an的前n项和Sn等于　　．‎ ‎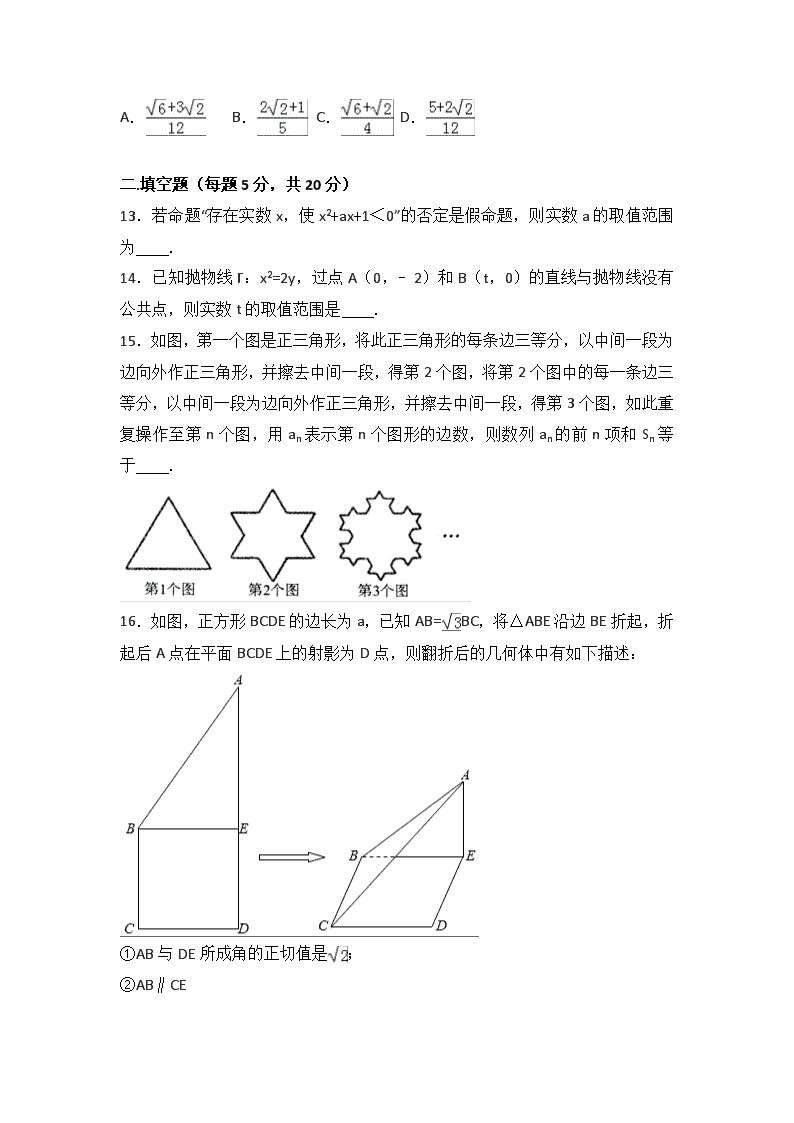16．如图，正方形BCDE的边长为a，已知AB=BC，将△ABE沿边BE折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：‎ ‎①AB与DE所成角的正切值是；‎ ‎②AB∥CE ‎③VB﹣ACE体积是a3；‎ ‎④平面ABC⊥平面ADC．‎ 其中正确的有　　．（填写你认为正确的序号）‎ ‎　‎ 三.解答题（请写出对应的文字说明，公式定理，解答过程，共6题，共70分）‎ ‎17．已知命题p：∃x0∈[﹣1，1]，满足x02+x0﹣a+1＞0，命题q：∀t∈（0，1），方程x2+=1都表示焦点在y轴上的椭圆．若命题p∨q为真命题，p∧q为假命题，求实数a的取值范围．‎ ‎18．如图，已知平面ABC⊥平面BCDE，△DEF与△ABC分别是棱长为1与2的正三角形，AC∥DF，四边形BCDE为直角梯形，DE∥BC，BC⊥CD，CD=1，点G为△ABC的重心，N为AB中点， =λ（λ∈r，λ＞0），‎ ‎（Ⅰ）当λ=时，求证：GM∥平面DFN ‎（Ⅱ）若直线MN与CD所成角为，试求二面角M﹣BC﹣D的余弦值．‎ ‎19．某市为了了解高二学生物理学习情况，在34所高中里选出5所学校，随机抽取了近千名学生参加物理考试，将所得数据整理后，绘制出频率分布直方图如图所示．‎ ‎（1）将34所高中随机编号为01，02，…，34，用下面的随机数表选取5组数抽取参加考试的五所学校，选取方法是从随机数表第一行的第6列和第7列数字开始，由左到右依次选取两个数字，则选出来的第4所学校的编号是多少？‎ ‎49 54 43 54 82 17 37 93 23 78 87 35 20‎ ‎96 43 84 26 34 91 64 57 24 55 06 88 77‎ ‎04 74 47 67 21 76 33 50 25 83 92 12 06‎ ‎（2）求频率分布直方图中a的值，试估计全市学生参加物理考试的平均成绩；‎ ‎（3）如果从参加本次考试的同学中随机选取3名同学，这3名同学中考试成绩在80分以上，（含80分）的人数记为X，求X的分布列及数学期望．（注：频率可以视为相应的概率）‎ ‎20．如图，在平面直角坐标系xOy中，椭圆C：的左焦点为F，右顶点为A，动点M为右准线上一点（异于右准线与x轴的交点），设线段FM交椭圆C于点P，已知椭圆C的离心率为，点M的横坐标为．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）若∠FPA为直角，求P点坐标；‎ ‎（3）设直线PA的斜率为k1，直线MA的斜率为k2，求k1•k2的取值范围．‎ ‎21．某旅游景区的观景台P位于高（山顶到山脚水平面M的垂直高度PO）为2km的山峰上，山脚下有一段位于水平线上笔直的公路AB，山坡面可近似地看作平面PAB，且△PAB为等腰三角形．山坡面与山脚所在水平面M所成的二面角为α（0°＜α＜90°），且sinα=．现从山脚的水平公路AB某处C0开始修建一条盘山公路，该公路的第一段、第二段、第三段…，第n﹣1段依次为 C0C1，C1C2，C2C3，…，Cn﹣1Cn（如图所示），且C0C1，C1C2，C2C3，…，Cn﹣1Cn与AB所成的角均为β，其中0＜β＜90°，sinβ=．试问：‎ ‎（1）每修建盘山公路多少米，垂直高度就能升高100米．若修建盘山公路至半山腰（高度为山高的一半），在半山腰的中心Q处修建上山缆车索道站，索道PQ依山而建（与山坡面平行，离坡面高度忽略不计），问盘山公路的长度和索道的长度各是多少？‎ ‎（2）若修建xkm盘山公路，其造价为a万元．修建索道的造价为2a万元/km．问修建盘山公路至多高时，再修建上山索道至观景台，总造价最少．‎ ‎22．已知函数f（x）=lnx．‎ ‎（1）求函数g（x）=f（x+1）﹣x的最大值；‎ ‎（2）若对任意x＞0，不等式f（x）≤ax≤x2+1恒成立，求实数a的取值范围；‎ ‎（3）若x1＞x2＞0，求证：＞．‎ ‎　‎ ‎2016-2017学年湖南省永州四中高二（上）期末数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一.选择题（每题5分，共60分）‎ ‎1．已知a，b∈R，则命题“若a2+b2=0，则a=0或b=0”的否命题是（　　）‎ A．若a2+b2≠0，则a≠0且b≠0 B．若a2+b2≠0，则a≠0或b≠0‎ C．若a≠0且b≠0，则a2+b2≠0 D．若a≠0或b≠0，则a2+b2≠0‎ ‎【考点】四种命题间的逆否关系．‎ ‎【分析】根据命题“若p，则q”的否命题是“若￢p，则￢q”，直接写出它的否命题即可．‎ ‎【解答】解：命题“若a2+b2=0，则a=0或b=0”的否命题是 ‎“若a2+b2≠0，则a≠0且b≠0”．‎ 故选：A．‎ ‎　‎ ‎2．双曲线=1的焦距为（　　）‎ A．2 B．4 C．2 D．4‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】直接利用双曲线方程，求出c，即可得到双曲线的焦距．‎ ‎【解答】解：双曲线=1，可知a2=10，b2=2，c2=12，‎ ‎∴c=2，2c=4．‎ 双曲线=1的焦距为：4．‎ 故选：D．‎ ‎　‎ ‎3．下列求导运算正确的是（　　）‎ A．（x）′=1 B．（x2cosx）′=﹣2xsinx C．（3x）′=3xlog3e D．（log2x）′=‎ ‎【考点】导数的运算．‎ ‎【分析】根据导数的运算公式和运算法则进行判断即可．‎ ‎【解答】解：A．（x+）′=1﹣，∴A错误．‎ B．（x2cosx）′=﹣2xsinx﹣x2sinx，∴B错误．‎ C．（3x）′=3xln3，∴C错误．‎ D．（log2x）′=，正确．‎ 故选：D．‎ ‎　‎ ‎4．在复平面内，复数i（2﹣i）对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【考点】复数的代数表示法及其几何意义．‎ ‎【分析】首先进行复数的乘法运算，得到复数的代数形式的标准形式，根据复数的实部和虚部写出对应的点的坐标，看出所在的象限．‎ ‎【解答】解：∵复数z=i（2﹣i）=﹣i2+2i=1+2i ‎∴复数对应的点的坐标是（1，2）‎ 这个点在第一象限，‎ 故选A．‎ ‎　‎ ‎5．若曲线处的切线与两坐标轴围成的三角形的面积为9，则a=（　　）‎ A．8 B．16 C．32 D．64‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】求得在点处的切线方程，可求三角形的面积，利用面积为9，即可求得a的值．‎ ‎【解答】解：求导数可得，所以在点处的切线方程为：‎ ‎，‎ 令x=0，得；令y=0，得x=3a．‎ 所以切线与两坐标轴围成的三角形的面积，解得a=16‎ 故选B．‎ ‎　‎ ‎6．某产品的广告费用x与销售额y的统计数据如下表 广告费用x（万元）‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y（万元）‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程=x+的为9.4，据此模型预报广告费用为6万元时销售额为（　　）‎ A．63.6万元 B．65.5万元 C．67.7万元 D．72.0万元 ‎【考点】线性回归方程．‎ ‎【分析】首先求出所给数据的平均数，得到样本中心点，根据线性回归直线过样本中心点，求出方程中的一个系数，得到线性回归方程，把自变量为6代入，预报出结果．‎ ‎【解答】解：∵=3.5，‎ ‎=42，‎ ‎∵数据的样本中心点在线性回归直线上，‎ 回归方程中的为9.4，‎ ‎∴42=9.4×3.5+a，‎ ‎∴=9.1，‎ ‎∴线性回归方程是y=9.4x+9.1，‎ ‎∴广告费用为6万元时销售额为9.4×6+9.1=65.5，‎ 故选：B．‎ ‎　‎ ‎7．某校在暑假组织社会实践活动，将8名高一年级学生，平均分配甲、乙两家公司，其中两名英语成绩优秀学生不能分给同一个公司；另三名电脑特长学生也不能分给同一个公司，则不同的分配方案有（　　）‎ A．36种 B．38种 C．108种 D．114种 ‎【考点】计数原理的应用．‎ ‎【分析】分类讨论：①甲部门要2个电脑特长学生和一个英语成绩优秀学生；②甲部门要1个电脑特长学生和1个英语成绩优秀学生．分别求得这2个方案的方法数，再利用分类计数原理，可得结论．‎ ‎【解答】解：由题意可得，有2种分配方案：①甲部门要2个电脑特长学生，则有3种情况；英语成绩优秀学生的分配有2种可能；再从剩下的3个人中选一人，有3种方法．‎ 根据分步计数原理，共有3×2×3=18种分配方案．‎ ‎②甲部门要1个电脑特长学生，则方法有3种；英语成绩优秀学生的分配方法有2种；再从剩下的3个人种选2个人，方法有33种，共3×2×3=18种分配方案．‎ 由分类计数原理，可得不同的分配方案共有18+18=36种，‎ 故选A．‎ ‎　‎ ‎8．空间四边形ABCD中，AB=CD，边AB．CD所在直线所成的角为30°，E、F分别为边BC、AD的中点，则直线EF与AB所成的角为（　　）‎ A．75° B．15° C．75°或15° D．90°‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】空间四边形ABCD中，AB=CD，边AB．CD所在直线所成的角为30°，E、F分别为边BC、AD的中点，则取BD中点为G，联结EG，FG，∵BG=GD，AF=FD，∠FGE的大小或补角等于异面直线AB与CD所成角的大小．‎ ‎【解答】‎ 解：由题意：AB=CD，边AB．CD所在直线所成的角为30°，E、F分别为边BC、AD的中点，取BD中点为G，联结EG，FG，‎ ‎∵BG=GD，AF=FD ‎∴，．‎ 所以∠FGE的大小或补角等于异面直线AB与CD所成角的大小，‎ 即∠FGE=30°或150°‎ 又AB=CD，∴FG=EG ‎∴△FGE为等腰三角形，∴∠GFE=75°，‎ ‎∴异面直线EF和AB所成角等于75°或15°．‎ 故选C．‎ ‎　‎ ‎9．已知F1、F2分别是双曲线﹣=1（a＞0，b＞0）的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆外，则双曲线离心率的取值范围是（　　）‎ A．（1，） B．（，+∞） C．（，2） D．（2，+∞）‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】根据斜率与平行的关系即可得出过焦点F2的直线，与另一条渐近线联立即可得到交点M的坐标，再利用点M在以线段F1F2为直径的圆外和离心率的计算公式即可得出．‎ ‎【解答】解：双曲线﹣=1的渐近线方程为y=±x，‎ 不妨设过点F2与双曲线的一条渐过线平行的直线方程为y=（x﹣c），‎ 与y=﹣x联立，可得交点M（，﹣），‎ ‎∵点M在以线段F1F2为直径的圆外，‎ ‎∴|OM|＞|OF2|，即有＞c2，‎ ‎∴b2＞3a2，‎ ‎∴c2﹣a2＞3a2，即c＞2a．‎ 则e=＞2．‎ ‎∴双曲线离心率的取值范围是（2，+∞）．‎ 故选：D．‎ ‎　‎ ‎10．如果函数满足：对于任意的x1，x2∈[0，1]，都有|f（x1）﹣f（x2）|≤1恒成立，则a的取值范围是（　　）‎ A． B． C． D．‎ ‎【考点】利用导数求闭区间上函数的最值．‎ ‎【分析】由题意函数满足：对于任意的x1，x2∈[0，1]，都有|f（x1）﹣f（x2）|≤1恒成立，必有函数满足其最大值与最小值的差小于等于1，由此不等式解出参数a的范围即可，故可先求出函数的导数，用导数判断出最值，求出最大值与最小值的差，得到关于a的不等式，解出a的值 ‎【解答】解：由题意f′（x）=x2﹣a2‎ 当a2≥1时，在x∈[0，1]，恒有导数为负，即函数在[0，1]上是减函数，故最大值为f（0）=0，最小值为f（1）=﹣a2，故有，解得|a|≤，故可得﹣≤a≤‎ 当a2∈[0，1]，由导数知函数在[0，a]上增，在[a，1]上减，故最大值为f（a）=又f（0）=0，矛盾，a∈[0，1]不成立，‎ 故选A．‎ ‎　‎ ‎11．如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1，CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（　　）‎ A． B． C． D．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】根据题意可设CB=1，CA=CC1=2，分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系，得到A、B、B1、C1四个点的坐标，从而得到向量与的坐标，根据异面直线所成的角的定义，结合空间两个向量数量积的坐标公式，可以算出直线BC1与直线AB1夹角的余弦值．‎ ‎【解答】解：分别以CA、CC1、CB为x轴、y轴和z轴建立如图坐标系，‎ ‎∵CA=CC1=2CB，∴可设CB=1，CA=CC1=2‎ ‎∴A（2，0，0），B（0，0，1），B1（0，2，1），C1（0，2，0）‎ ‎∴=（0，2，﹣1），=（﹣2，2，1）‎ 可得•=0×（﹣2）+2×2+（﹣1）×1=3，且=， =3，‎ 向量与所成的角（或其补角）就是直线BC1与直线AB1夹角，‎ 设直线BC1与直线AB1夹角为θ，则cosθ==‎ 故选A ‎　‎ ‎12．如图，正四面体ABCD的顶点C在平面α内，且直线BC与平面α所成角为45°，顶点B在平面α上的射影为点O，当顶点A与点O的距离最大时，直线CD与平面α所成角的正弦值等于（　　）‎ A． B． C． D．‎ ‎【考点】直线与平面所成的角．‎ ‎【分析】由题意，可得当O、B、A、C四点共面时顶点A与点O的距离最大，设此平面为β．由面面垂直判定定理结合BO⊥α，证出β⊥α．过D作DE⊥α于E，连结CE，根据面面垂直与线面垂直的性质证出DH∥α，从而点D到平面α的距离等于点H到平面α的距离．设正四面体ABCD的棱长为1，根据BC与平面α所成角为45°和正四面体的性质算出H到平面α的距离，从而在Rt△CDE中，利用三角函数的定义算出sin∠DCE=，即得直线CD与平面α所成角的正弦值．‎ ‎【解答】解：∵四边形OBAC中，顶点A与点O的距离最大，‎ ‎∴O、B、A、C四点共面，设此平面为β ‎∵BO⊥α，BO⊂β，∴β⊥α 过D作DH⊥平面ABC，垂足为H，‎ 设正四面体ABCD的棱长为1，则Rt△HCD中，CH=BC=‎ ‎∵BO⊥α，直线BC与平面α所成角为45°，‎ ‎∴∠BCO=45°，结合∠HCB=30°得∠HCO=75°‎ 因此，H到平面α的距离等于HCsin75°=×=‎ 过D作DE⊥α于E，连结CE，则∠DCE就是直线CD与平面α所成角 ‎∵DH⊥β，α⊥β且DH⊄α，∴DH∥α 由此可得点D到平面α的距离等于点H到平面α的距离，即DE=‎ ‎∴Rt△CDE中，sin∠DCE==，即直线CD与平面α所成角的正弦值等于 故选：A ‎　‎ 二.填空题（每题5分，共20分）‎ ‎13．若命题“存在实数x，使x2+ax+1＜0”的否定是假命题，则实数a的取值范围为　a＜﹣2或a＞2　．‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】特称命题的否定是假命题，即原命题为真命题，得到判别式大于0，解不等式即可．‎ ‎【解答】解：∵命命题“存在实数x，使x2+ax+1＜0”的否定是假命题，‎ ‎∴原命题为真命题，即“存在实数x，使x2+ax+1＜0”为真命题，‎ ‎∴△=a2﹣4＞0‎ ‎∴a＜﹣2或a＞2‎ 故答案为：a＜﹣2或a＞2‎ ‎　‎ ‎14．已知抛物线Г：x2=2y，过点A（0，﹣2）和B（t，0）的直线与抛物线没有公共点，则实数t的取值范围是　（﹣∞，﹣1）∪（1，+∞）　．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】设过A的直线方程，与抛物线方程联立，根据判别式求得k，求得过A的抛物线的切线与y=0的交点，则当过点A（0，﹣2）和B（t，0）的直线与抛物线C没有公共点，进而求得t的范围．‎ ‎【解答】解：设过A的直线方程为y=kx﹣2，与抛物线方程联立得x2﹣2kx+4=0，‎ ‎△=4k2﹣16=0，k=±2，求得过A的抛物线的切线与y=0的交点为（±1，0），‎ 则当过点A（0，﹣2）和B（t，0）的直线与抛物线C没有公共点，‎ 实数t的取值范围是（﹣∞，﹣1）∪（1，+∞），‎ 故答案为：（﹣∞，﹣1）∪（1，+∞）．‎ ‎　‎ ‎15．如图，第一个图是正三角形，将此正三角形的每条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第2个图，将第2个图中的每一条边三等分，以中间一段为边向外作正三角形，并擦去中间一段，得第3个图，如此重复操作至第n个图，用an表示第n个图形的边数，则数列an的前n项和Sn等于　4n﹣1　．‎ ‎【考点】等比数列的前n项和．‎ ‎【分析】根据图形得到，a1=3，a2=12，a3=48，由题意知：每一条边经一次变化后总变成四条边，即，由等比数列的定义知：an=3×4n﹣1，于是根据等比数列前n项和公式即可求解 ‎【解答】解：∵a1=3，a2=12，a3=48‎ 由题意知：每一条边经一次变化后总变成四条边，即，‎ 由等比数列的定义知：an=3×4n﹣1‎ ‎∴Sn==4n﹣1‎ 故答案为：4n﹣1‎ ‎　‎ ‎16．如图，正方形BCDE的边长为a，已知AB=BC，将△ABE沿边BE折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：‎ ‎①AB与DE所成角的正切值是；‎ ‎②AB∥CE ‎③VB﹣ACE体积是a3；‎ ‎④平面ABC⊥平面ADC．‎ 其中正确的有　①③④　．（填写你认为正确的序号）‎ ‎【考点】棱柱、棱锥、棱台的体积．‎ ‎【分析】作出直观图，逐项进行分析判断．‎ ‎【解答】解：作出折叠后的几何体直观图如图所示：‎ ‎∵AB=a，BE=a，∴AE=．‎ ‎∴AD=．∴AC=．‎ 在△ABC中，cos∠ABC===．‎ ‎∴sin∠ABC==．‎ ‎∴tan∠ABC==．‎ ‎∵BC∥DE，∴∠ABC是异面直线AB，DE所成的角，故①正确．‎ 连结BD，CE，则CE⊥BD，‎ 又AD⊥平面BCDE，CE⊂平面BCDE，‎ ‎∴CE⊥AD，又BD∩AD=D，BD⊂平面ABD，AD⊂平面ABD，‎ ‎∴CE⊥平面ABD，又AB⊂平面ABD，‎ ‎∴CE⊥AB．故②错误．‎ 三棱锥B﹣ACE的体积V===，故③正确．‎ ‎∵AD⊥平面BCDE，BC⊂平面BCDE，‎ ‎∴BC⊥AD，又BC⊥CD，‎ ‎∴BC⊥平面ACD，∵BC⊂平面ABC，‎ ‎∴平面ABC⊥平面ACD．‎ 故答案为①③④．‎ ‎　‎ 三.解答题（请写出对应的文字说明，公式定理，解答过程，共6题，共70分）‎ ‎17．已知命题p：∃x0∈[﹣1，1]，满足x02+x0﹣a+1＞0，命题q：∀t∈（0，1），方程x2+=1都表示焦点在y轴上的椭圆．若命题p∨q为真命题，p∧q为假命题，求实数a的取值范围．‎ ‎【考点】复合命题的真假．‎ ‎【分析】在命题p中，因为∃x0∈[﹣1，1]，满足，所以只要的最大值满足不等式即可，这样求出该最大值，即可得到a的取值范围．同样根据命题q中的方程表示椭圆，求出a的取值范围．容易判断命题p和q中一真一假，所以分p真，q假和p假，q真讨论，求对应的a的取值范围，然后求这两种情况的并集即可．‎ ‎【解答】解：因为∃x0∈[﹣1，1]，满足，所以只须；‎ ‎∵，∴x0=1时，的最大值为3﹣a，∴3﹣a＞0，所以命题p：a＜3；‎ 因为∀t∈（0，1），方程都表示焦点在y轴上的椭圆，所以t2﹣（2a+‎ ‎2）t+a2+2a+1＞1即t2﹣（2a+2）t+a2+2a=（t﹣a）（t﹣（a+2））＞0对t∈（0，1）恒成立，只须a+2≤0或a≥1，得a≤﹣2或a≥1；‎ 根据已知条件知，p和q中一真一假：‎ 若p真q假，得，即﹣2＜a＜1；‎ 若p假q真，得，得a≥3‎ 综上所述，﹣2＜a＜1，或a≥3；‎ ‎∴a的取值范围为（﹣2，1）∪[3，+∞）．‎ ‎　‎ ‎18．如图，已知平面ABC⊥平面BCDE，△DEF与△ABC分别是棱长为1与2的正三角形，AC∥DF，四边形BCDE为直角梯形，DE∥BC，BC⊥CD，CD=1，点G为△ABC的重心，N为AB中点， =λ（λ∈r，λ＞0），‎ ‎（Ⅰ）当λ=时，求证：GM∥平面DFN ‎（Ⅱ）若直线MN与CD所成角为，试求二面角M﹣BC﹣D的余弦值．‎ ‎【考点】二面角的平面角及求法；直线与平面平行的判定．‎ ‎【分析】（Ⅰ）当λ=时，连AG延长交BC于P，证明GM∥PF，P，D，F，N四点共面，即可证明：GM∥平面DFN ‎（Ⅱ）若直线MN与CD所成角为，以P为原点，PC为x轴，PE为y轴，PA为z轴建立空间直角坐标系，利用向量的夹角公式求二面角M﹣BC﹣D的余弦值．‎ ‎【解答】（Ⅰ）证明：连AG延长交BC于P，‎ 因为点G为△ABC的重心，所以=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 又=λ，λ=，所以==，所以GM∥PF；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 因为AC∥DF，DE∥BC，所以平面ABC∥平面DEF，‎ 又△DEF与△ABC分别是棱长为1与2的正三角形，N为AB中点，P为BC中点，所以NP∥AC，‎ 又AC∥DF，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 所以NP∥DF，得P，D，F，N四点共面 ‎∴GM∥平面DFN﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎（Ⅱ）平面ABC⊥平面BCDE，易得平面DEF⊥平面BCDE，‎ 以P为原点，PC为x轴，PE为y轴，PA为z轴建立空间直角坐标系，‎ 则C（1，0，0），D（1，1，0），A（0，0，），F（，1，），B（﹣1，0，0），N（﹣，0，），﹣﹣﹣﹣‎ 设M（x，y，z），‎ ‎∵=λ，∴M（，λ，），=（，λ，），=（0，1，0）‎ 因为MN与CD所成角为，所以=，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 得2λ2+λ﹣1=0，∴λ=，∴M（，，），‎ 设平面MBC的法向量=（a，b，c），=（2，0，0），=（，，），‎ 则，取=（0，3，﹣2），‎ 面BCD的法向量=（0，0，1），所以二面角M﹣BC﹣D的余弦值==﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎　‎ ‎19．某市为了了解高二学生物理学习情况，在34所高中里选出5所学校，随机抽取了近千名学生参加物理考试，将所得数据整理后，绘制出频率分布直方图如图所示．‎ ‎（1）将34所高中随机编号为01，02，…，34，用下面的随机数表选取5组数抽取参加考试的五所学校，选取方法是从随机数表第一行的第6列和第7列数字开始，由左到右依次选取两个数字，则选出来的第4所学校的编号是多少？‎ ‎49 54 43 54 82 17 37 93 23 78 87 35 20‎ ‎96 43 84 26 34 91 64 57 24 55 06 88 77‎ ‎04 74 47 67 21 76 33 50 25 83 92 12 06‎ ‎（2）求频率分布直方图中a的值，试估计全市学生参加物理考试的平均成绩；‎ ‎（3）如果从参加本次考试的同学中随机选取3名同学，这3名同学中考试成绩在80分以上，（含80分）的人数记为X，求X的分布列及数学期望．（注：频率可以视为相应的概率）‎ ‎【考点】离散型随机变量的期望与方差；频率分布直方图；离散型随机变量及其分布列．‎ ‎【分析】（1）由已知条件利用随机数法能求出第4所学校的编号．‎ ‎（2）由频率分布直方图的性质得2a+2a+3a+6a+7a=20a，由此能求出a=0.005，从而能估计全市学生参加物理考试的平均成绩．‎ ‎（3）从参加考试的同学中随机抽取1名同学的成绩在80分以上的概率为，X可能的取值是0，1，2，3，分别求出相应的概率，由此能求出X的分布列及数学期望．‎ ‎【解答】解：（1）将34所高中随机编号为01，02，…，34，‎ 用题中所给随机数表选取5组数抽取参加考试的五所学校，选取方法是从随机数表第一行的第6列和第7列数字开始，‎ 由左到右依次选取两个数字，则选出来的五所学校依次为：21，32，09，16，17．‎ ‎∴第4所学校的编号是16．‎ ‎（2）由频率分布直方图的性质得：‎ ‎2a+2a+3a+6a+7a=20a，20a×10=1，‎ 解得a=0.005，‎ 估计全市学生参加物理考试的平均成绩为：‎ ‎0.1×55+0.15×65+0.35×75+03×85+0.1×95=76.5‎ ‎（3）从参加考试的同学中随机抽取1名同学的成绩在80分以上的概率为 X可能的取值是0，1，2，3‎ P（X=0）=，‎ P（X=1）=，‎ P（X=2）=，‎ P（X=3）=，‎ ‎∴X的分布列为：‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以E（X）=0×（或X～B（3，），所以E（X）=np=3×=）．‎ ‎　‎ ‎20．如图，在平面直角坐标系xOy中，椭圆C：的左焦点为F，右顶点为A，动点M为右准线上一点（异于右准线与x轴的交点），设线段FM交椭圆C于点P，已知椭圆C的离心率为，点M的横坐标为．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）若∠FPA为直角，求P点坐标；‎ ‎（3）设直线PA的斜率为k1，直线MA的斜率为k2，求k1•k2的取值范围．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由椭圆的离心率e==，准线方程x==，即可求得a和c的值，则b2=a2﹣c2=5，即可求得椭圆C的标准方程；‎ ‎（2）由∠FPA为直角，以AF为直径的圆的与椭圆相交于P点，设P（x，±‎ ‎），求得圆心为O（，0）及半径为，根据点到直线的距离公式，即可求得a的值，代入求得y的值，即可求得P点坐标；‎ ‎（3）设点P（x1，y1）（﹣2＜x1＜3），点M，由点F、P、M三点共线，求得点M的坐标，．，则．由此可导出k1•k2的取值范围．‎ ‎【解答】解：（1）由题意可知：离心率e==，‎ 准线方程x==，‎ 解得：a=3，c=2，‎ 由b2=a2﹣c2=5，‎ ‎∴求椭圆C的标准方程为；…‎ ‎（2）由∠FPA为直角，‎ ‎∴以AF为直径的圆的与椭圆相交于P点，设P（x，±），‎ ‎∴圆心为O（，0），半径为，‎ ‎∴丨PO丨=，即=，整理得：4x2﹣9x﹣9=0，‎ 解得：x=﹣或x=3（舍去），‎ ‎∴y=±=±，‎ ‎∴P点坐标为：…‎ ‎（3）设点P（x1，y1）（﹣2＜x1＜3），点，‎ ‎∵点F，P，M共线，x1≠﹣2，‎ ‎∴，即，‎ ‎∴，…‎ ‎∵，‎ ‎∴，…‎ 又∵点P在椭圆C上，‎ ‎∴，‎ ‎∴，…‎ ‎∵﹣2＜x1＜3，‎ ‎∴，‎ 故k1•k2的取值范围为…‎ ‎　‎ ‎21．某旅游景区的观景台P位于高（山顶到山脚水平面M的垂直高度PO）为2km的山峰上，山脚下有一段位于水平线上笔直的公路AB，山坡面可近似地看作平面PAB，且△PAB为等腰三角形．山坡面与山脚所在水平面M所成的二面角为α（0°＜α＜90°），且sinα=．现从山脚的水平公路AB某处C0开始修建一条盘山公路，该公路的第一段、第二段、第三段…，第n﹣1段依次为 C0C1，C1C2，C2C3，…，Cn﹣1Cn（如图所示），且C0C1，C1C2，C2C3，…，Cn﹣1Cn与AB所成的角均为β，其中0＜β＜90°，sinβ=．试问：‎ ‎（1）每修建盘山公路多少米，垂直高度就能升高100米．若修建盘山公路至半山腰（高度为山高的一半），在半山腰的中心Q处修建上山缆车索道站，索道PQ依山而建（与山坡面平行，离坡面高度忽略不计），问盘山公路的长度和索道的长度各是多少？‎ ‎（2）若修建xkm盘山公路，其造价为a万元．修建索道的造价为2a万元/km．问修建盘山公路至多高时，再修建上山索道至观景台，总造价最少．‎ ‎【考点】解三角形的实际应用；函数模型的选择与应用；利用导数求闭区间上函数的最值．‎ ‎【分析】（1）在盘山公路上取一个点，作出该点到平面的垂线，再利用三垂线定理作出二面角棱的垂线，连接两个垂足，利用三角函数的定义可求出索道长与山高的倍数关系，得出结论；‎ ‎（2）设盘山公路修至山高的距离为x，建立关于x的函数，利用导数确定函数的单调性，极小值即为函数的最小值，从而得出最少总价对应的x．‎ ‎【解答】解：（1）在盘山公路C0C1上任选一点D，作DE⊥平面M交平面M于E，过E作EF⊥AB交AB于F，连接DF，易知DF⊥C0F．sin∠DFE=，sin∠DC0F=．‎ ‎∵DF=C0D，DE=DF，∴DE=C0D，‎ 所以盘山公路长度是山高的10倍，索道长是山高的倍，‎ 所以每修建盘山公路1000米，垂直高度升高100米．‎ 从山脚至半山腰，盘山公路为10km．从半山腰至山顶，索道长2.5km．‎ ‎（2）设盘山公路修至山高x（0＜x＜2）km，则盘山公路长为10xkm，索道长（2﹣x）km．‎ 设总造价为y万元，‎ 则y=a+（2﹣x）•2a=（10﹣5x）a+10a．‎ 令y′=﹣5a=0，则x=1．‎ 当x∈（0，1）时，y′＜0，函数y单调递减；当x∈（1，2）时，y′＞0，函数y单调递增，‎ ‎∴x=1，y有最小值，即修建盘山公路至山高1km时，总造价最小，最小值为15a万元．‎ ‎　‎ ‎22．已知函数f（x）=lnx．‎ ‎（1）求函数g（x）=f（x+1）﹣x的最大值；‎ ‎（2）若对任意x＞0，不等式f（x）≤ax≤x2+1恒成立，求实数a的取值范围；‎ ‎（3）若x1＞x2＞0，求证：＞．‎ ‎【考点】导数在最大值、最小值问题中的应用．‎ ‎【分析】（1）先求出g（x）=ln（x﹣1）﹣x（x＞﹣1），然后求导确定单调区间，极值，最值即可求．‎ ‎（2）本小题转化为在x＞0上恒成立，进一步转化为，然后构造函数h（x）=，利用导数研究出h（x）的最大值，再利用基础不等式可知，从而可知a的取值范围．‎ ‎（3）本小题等价于．令t=，设u（t）=lnt﹣，t＞1，由导数性质求出u（t）＞u（1）=0，由此能够证明＞．‎ ‎【解答】解：（1）∵f（x）=lnx，‎ ‎∴g（x）=f（x+1）﹣x=ln（x+1）﹣x，x＞﹣1，‎ ‎∴．‎ 当x∈（﹣1，0）时，g′（x）＞0，∴g（x）在（﹣1，0）上单调递增；‎ 当x∈（0，+∞）时，g′（x）＜0，则g（x）在（0，+∞）上单调递减，‎ ‎∴g（x）在x=0处取得最大值g（0）=0．‎ ‎（2）∵对任意x＞0，不等式f（x）≤ax≤x2+1恒成立，‎ ‎∴在x＞0上恒成立，‎ 进一步转化为，‎ 设h（x）=，则，‎ 当x∈（1，e）时，h′（x）＞0；当x∈（e，+∞）时，h′（x）＜0，‎ ‎∴h（x）．‎ 要使f（x）≤ax恒成立，必须a．‎ 另一方面，当x＞0时，x+，‎ 要使ax≤x2+1恒成立，必须a≤2，‎ ‎∴满足条件的a的取值范围是[，2]．‎ ‎（3）当x1＞x2＞0时，＞等价于．‎ 令t=，设u（t）=lnt﹣，t＞1‎ 则＞0，‎ ‎∴u（t）在（1，+∞）上单调递增，‎ ‎∴u（t）＞u（1）=0，‎ ‎∴＞．‎ ‎　‎