数学理（B）卷·2019届北京人大附中高二上学期期末考试仿真卷（2018-01） 17页

2017-2018 学年上学期高二年级期末考试仿真测试卷 理 科 数 学 （B） 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证 号条形码粘贴在答题卡上的指定位置。 2．选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案 标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题 卷、草稿纸和答题卡上的非答题区域均无效。 4．考试结束后，请将本试题卷和答题卡一并上交。 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项 中，只有一项是符合题目要求的． 1．[2017·思南中学]若 ，则下列不等式中不成立的是（ ） A． B． C． D． 2．[2017·珠海一中]若 ， 满足 ，则 的最大值为（ ） A． B． C．1 D．2 3 ． [2017· 三 明 期 末 ] 若 关 于 的 一 元 二 次 不 等 式 的 解 集 是 ，则 的最小值是（ ） A． B． C． D． 4．[2017·莆田六中]已知数列 是首项为 1，公差为 的等差数列，若 81 是该数列中的一项，则公差 不可能是（ ） A．2 B．3 C．4 D．5 0a b< < a b> 1 1 a b a >− 1 1 a b > 2 2a b> x y 1 2 0 3 2 2 0 x y x y x y    + − − + ≥ ≤ ≥ 3z x y= − 1 3 2 3 x 2 23 2 0x ax a− + ≥ ( ] [ )( )1 2 1 2,, x x x x−∞ +∞ ≠ ( )1 2 1 2 1a x x x x + + 3 2 3 2 6 3 6 { }na ( )*d d ∈N d 此 卷 只 装 订 不 密 封 班级 姓名 准考证号 考场号 座位号 5．[2017·横峰中学] “不等式 在 上恒成立”的一个必要不充分条件 是（ ） A． B． C． D． 6．[2017·云南一检]已知等比数列 的前 项和为 ，若 ， ，则 数列 的前 项和为（ ） A． B． C． D． 7．[2017·福州教育学院附中]如图，空间四边形 中， ， ， ，点 在 上， ，点 为 中点，则 等于（ ） A． B． C． D． 8 ． [2017· 玉 山 一 中 ] 在 中 ， 为 边 上 一 点 ， ， ， ，若 ，则 的值为（ ） A． B． C． D． 9．[2017·南昌二中]正四棱柱 中，底面边长为 2，侧棱长为 4， 则 点到平面 的距离为（ ） A． B． C． D． 10．[2017·成都七中]已知 ， 为双曲线 的左右焦点，过 的直线 与圆 相切于点 ，且 ，则直线 的斜率是（ ） 2 0x x m− + > R 1 4m > 0m > 0 1m< < 1m > { }na n nS 3 7S = 6 63S = { }nna n ( )3 1 2nn− + + × ( )3 1 2nn+ + × ( )1 1 2nn+ + × ( )1 1 2nn+ − × OABC aOA =  bOB =  cOC =  M OA 2 3OM OA=  N BC MN 1 2 1 2 3 2a b c− +  2 1 1 3 2 2a b c− + +  1 1 1 2 2 2a b c+ −  2 2 1 3 3 2a b c+ −  ABC△ D BC 1 2BD DC= 120ADB∠ = ° 2AD = 3 3ADCS = −△ sin BAC∠ 6 3 6 2 4 + 2 3 5 3 2 1 1 1 1ABCD A B C D− 1B 1AD C 8 3 2 2 3 4 2 3 4 3 1F 2F 2 2 2 2 1( , 0)x y a ba b − = > 1F l 2 2 2x y b+ = M 2 12MF MF= l A． B． C． D． 11．[2017·南溪二中]已知椭圆 ，点 ， 为长轴的两个 端点，若在椭圆上存在点 ，使 ，则离心率 的取值范围为（ ） A． B． C． D． 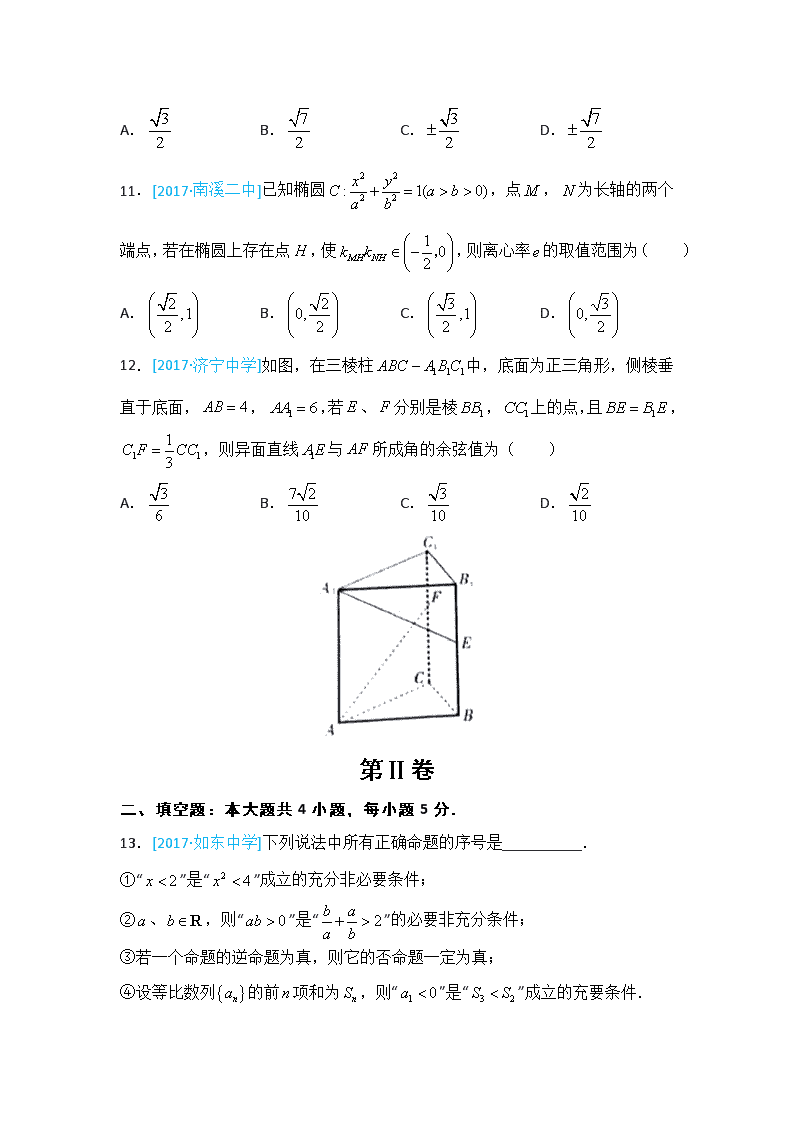12．[2017·济宁中学]如图，在三棱柱 中，底面为正三角形，侧棱垂 直于底面， ， ，若 、 分别是棱 ， 上的点，且 ， ，则异面直线 与 所成角的余弦值为（ ） A． B． C． D． 第Ⅱ卷 二、填空题：本大题共 4 小题，每小题 5 分． 13．[2017·如东中学]下列说法中所有正确命题的序号是__________． ①“ ”是“ ”成立的充分非必要条件； ② 、 ，则“ ”是“ ”的必要非充分条件； ③若一个命题的逆命题为真，则它的否命题一定为真； ④设等比数列 的前 项和为 ，则“ ”是“ ”成立的充要条件． 3 2 7 2 3 2 ± 7 2 ± 2 2 2 2: 1( 0)x yC a ba b + = > > M N H 1 02MH NHk k  ∈ −  ， e 2 ,12       20, 2       3 ,12       30, 2       1 1 1ABC A B C− 4AB = 1 6AA = E F 1BB 1CC 1BE B E= 1 1 1 3C F CC= 1A E AF 3 6 7 2 10 3 10 2 10 2x < 2 4x < a b∈R 0ab > 2b a a b + > { }na n nS 1 0a < 3 2S S< 14．[2017·舒兰中学]给出下列命题：① ，且 ， ；② ， 使得 ；③若 ， ，则 ；④当 时，不等 式 恒成立，则实数 的取值范围是 ．其中所有真命题的序 号是__________． 15．[2017·石室中学]椭圆 的左、右焦点分别为 ， ，弦 过 ， 若 的内切圆的周长为 ， ， 两点的坐标分别为 ， ，则 ____． 16．[2017·闽侯八中]在四棱锥 中，平面 平面 ，侧面 是 边长为 的等边三角形，底面 是矩形，且 ，则该四棱锥外接球 的表面积等于__________． 三、解答题：解答应写出文字说明、证明过程或演算步骤． 17．[2017·北京四中]已知集合 ， ， ． （1）求 ； （2）已知 ， ，若 是 的充分不必要条件，求 的取值范围． 18．[2017·新乡期末]在 中，角 ， ， 所对的边分别为 ， ， ，已 x∀ ∈R 0x ≠ 1 2x x + ≥ x∃ ∈R 2 1 2x x+ ≤ 0x > 0y > 2 2 2 2 x y xy x y + +≥ ( )1,2x∈ 2 4 0x mx+ + < m 5m −≤ 2 2 125 16 x y+ = 1F 2F AB 1F 2ABF△ 2π A B ( )1 1,x y ( )2 2,x y 2 1y y− = S ABCD− SAB ⊥ SAD SAB 2 3 ABCD 4BC = 2{ | 10 21 0}A x x x= − + < 2 2{ |1 log log 10}B x x= < < { | 2 2 }x aC x= < ( )A BR  :q x C∈ :p x A∈ p q a ABC△ A B C a b c 知 ． （1）求角 的大小； （2）若 ， ，求边 的长． 19．[2017·中原名校]已知数列 的前 项和为 ． （1）求数列 的通项公式； （2）令 ，求数列 的前 项和 ． 20．[2017·南昌二中]某家具厂有方木料 ，五合板 ，准备加工成书桌 和书橱出售．已知生产每张书桌需要方木料 ，五合板 ，生产每个书橱 需要方木料 ，五合板 ，出售一张书桌可获利润 元，出售一个书橱可 cos cos 2 cosa B b A c C+ = C 5a = 8b = c { }na n 3 1n nS = + { }na n n nb a = { }nb n nT 390m 2600m 30.1m 22m 30.2m 21m 80 获利润 元． （1）如果只安排生产书桌，可获利润多少? （2）如果只安排生产书橱，可获利润多少? （3）怎祥安排生产可使所得利润最大? 21．[2017·贵阳一中]已知椭圆 的离心率为 ， ， 是 椭圆的左、右焦点， 是椭圆上一点， 的最小值为 2． （1）求椭圆 的方程； （2）过点 且与 轴不重合的直线 交椭圆 于 ， 两点，圆 是以 为圆 心椭圆 的长轴长为半径的圆，过 且与 垂直的直线与圆 交于 ， 两点， 求四边形 面积的取值范围． 120 ( )2 2 2 2: 1 0x yC a ba b + = > > 1 2 1F 2F P 1 2PF PF⋅  C 2F x l C M N E 1F C 2F l E P Q MPNQ 22．[2017·福建师范附中]已知四棱锥 ，底面 是边长为 的菱形， ， 为 的中点， 平面 ， 与平面 所成角的正 弦值为 ． （1）在棱 上求一点 ，使 平面 ； （2）求二面角 的余弦值． 2017-2018 学年上学期高二年级期末考试仿真测试 卷 理 科 数 学 （B）答 案 第Ⅰ卷 一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项 中，只有一项是符合题目要求的． 1．【答案】B 【解析】∵ ，∴ ，∴ ，因此 B 不正确． 2．【答案】D 【解析】由约束条件 作出可行域如图，联立 ，解 得 ，化目标函数 为 ，由图可知，当直线 过 P ABCD− ABCD 2 60ABC∠ = ° E AB PA ⊥ ABCD PC PAD 6 4 PD F //AF PEC D PE A− − 0a b< < 0a a b< − < 1 1 a b a <− 1 2 0 3 2 2 0 x y x y x y    + − − + ≥ ≤ ≥ 3 2 2 0 2 2 x y x y − + =  − = ( )2,4A 3z x y= − 3y x z= − 3z x y= − A 时可知取得最大值，代入得 2． 3．【答案】D 【 解 析 】 ∵ 关 于 的 一 元 二 次 不 等 式 的 解 集 是 ，∴ ，∴ ， ， ∴ ，当且仅当 时取等号． ∴ 的最小值是 ． 4．【答案】B 【解析】由题设， ，81 是该数列中的一项，即 ， 所以 ，因为 ， ，所以 是 80 的因数，故 不可能是 3，选 B． 5．【答案】B 【解析】“不等式 在 上恒成立”的等价条件为 ，即 ，所以必要不充分条件比 的范围更大且包含 ，所以选 B． 6．【答案】D 【 解 析 】 当 时 ， 不 成 立 ， 当 时 ， ， 两 式 相 除 得 ，解得： ， 即 ， ， x 2 23 2 0x ax a− + ≥ ( ] [ )( )1 2 1 2,, x x x x−∞ +∞ ≠ 2 2 29 8 0a a a∆ = − = > 1 2 3x x a+ = 2 1 2 2x x a= ( ) 2 1 2 2 1 2 1 13 62a x x ax x a + + = + ≥ 4 1 6a = ( )1 2 1 2 1a x x x x + + 6 ( )1 1na n d= + − ( )81 1 1n d= + − 80 1n d = + d *n∈N d d 2 0x x m− + > R 1 4 0m∆ = − < 1 4m > 1 4m > 1 4m > 1q = 1q ≠ ( ) ( ) 3 1 6 1 1 71 1 631 a q q a q q  −  =− − = − 3 6 3 1 1 7 1 1 63 q q q − = =− + 2q = 1 1a = 1 1 1 2n n na a q − −= = 12n nn a n −⋅ = ⋅ 设数列 的前 项和为 ，则 ， ， 两式相减得到： ， 所以 ，故选 D． 7．【答案】B 【解析】由题意 ； 又 ， ， ， ．故选 B． 8．【答案】D 【解析】设 ，则 ， ，则 ， ， ， ， ， ， ， ， ， ，选 D． 9．【答案】A 【解析】根据题意，以 为原点， ， ， 分别为 ， ， 为坐标轴， 建立空间直角坐标系，则 ， ， ， ，设平面 的 法 向 量 为 ， 则 ， 取 ， 则 ，所以 ，所以 点到平面 的距离为 ，故选 { }nna n nT 2 11 2 2 3 2 ...... 2n nT n −= + ⋅ + ⋅ + + ⋅ ( )2 12 1 2 2 2 ...... 1 2 2n n nT n n−= ⋅ + ⋅ + + − ⋅ + ⋅ ( )2 1 1 21 2 2 ...... 2 2 2 1 2 11 2 n n n n n nT n n n− −− = + + + + − ⋅ = − ⋅ = − ⋅ −− ( )1 1 2n nT n= + − × 1 1 3 2MN MA AB BN OA OB OA BC= + + = + − +        2 1 1 2 1 1 3 2 2 3 2 2OA OB OC OB OA OB OC= − + + − = − + +       aOA =  bOB =  cOC =  2 1 1 3 2 2MN a b c∴ = − + +   BD x= 2CD x= 120ADB∠ = ° 60ADC∠ = ° 1 sin 3 3 32ADCS AD DC ADC x= ⋅ ∠ = = −△ 3 1x = − 1 3 3 2 2ADB ADCS S −= =△ △ 9 3 3 2ABCS −=△ 2 2 2 2 cos 6AB AD BD AD BD ADB= + − ⋅ ∠ = 6AB = 2 2 2 2 cos 24 12 3AC AD CD AD CD ADC= + − ⋅ ∠ = − 2 6 3 3AC = − 9 3 3 2 3sin 1 2 26 2 6 3 3·2 ABCSBAC AB AC −∠ = = ⋅ = ⋅ − △ D DA DC 1DD x y z ( )2,0,0A ( )0,2,0C ( )1 0,0,4D ( )1 2,2,4B 1AD C ( ), ,n x y z= 1 0 2 4 0 2 2 00 n AC x z x yn AD  ⋅ = − + = ⇒ − + =⋅ =    1z = 2x y= = ( )2,2,1n = 1B 1AD C 1 1 8 3 n B D n ⋅ =   A． 10．【答案】C 【解析】由题意得 ， 在 中由余弦定理得： ， 选 C． 11．【答案】A 【解析】由题意 ， ．设 ，则 ． ， 可得： ， ．故选 A． 12．【答案】D 【解析】以 的中点为原点建立如图所示的空间直角坐标系， 因为 ， ，且 ， ， 所以 ， ， ， ， 所以 ， ， 则 ， 所以异面直线 与 所成的角的余弦值为 ，故选 D． 第Ⅱ卷 二、填空题：本大题共 4 小题，每小题 5 分． 13．【答案】②③④ 2 2 2 2 1 1 2 2MF OF OM c b a MF a= − = − = ⇒ = 2MF O△ ( )22 2 2 2 2 1 2 3cos cos 3 42 2l b c ab bMOF MOF a b kc bc a + −∠ = − ∠ = − = ⇒ = ⇒ = ± = ± ( ),0M a− ( ),0N a ( )0 0,H x y 2 2 2 2 0 02 ( )by a xa = − 2 2 2 2 2020 0 0 2 2 2 2 2 0 0 0 0 ( ) 1 ,02MH NH b a xy y y bak k x a x a x a x a a −  ∴ = ⋅ = = = − ∈ − + − − −   2 2 2 2 11 ,02 c a ea −  = − ∈ −   2 ,12e  ∴ ∈    AB 4AB = 1 6AA = 1BE B E= 1 1 1 3C F CC= ( )0, 2,0A − ( )1 0, 2,6A − ( )0,2,3E ( )2 3,0,4F − ( )1 0, 2,0A E = − ( )2 3,2,4AF = − 1 1 1 4 2cos< , > 105 4 2 A E AFA E AF A E AF ⋅ −= = = − ×⋅      1A E AF 2 10 【解析】对于①中， ，则 ，所以 是 的必要不充分条 件，所以不正确； 对 于 ② 中 ， 由 时 ， 则 ， 而 当 ，则 成立，所以 是 的 必要不充分条件，所以②正确； 对于③中，原命题的逆命题与原命题的否命题，互为逆否关系，所以一个命题的 逆命题为真，则它的否命题一定为真是正确的，所以③正确； 对于④中，在等比数列中，当 时， ，即 成立， 当 时，则 ，所以 ，所以在等比数列中， 是 的充要条件，所以④是正确的，故填②③④． 14．【答案】②③④ 【解析】①令 ，可得 ，故①错误； ， ， ，令 ，可得 ，故②正确； ， ，由已知均值不等式 ， ，故③正确； ④取 ， ， ， ，故④正确． 所以其中真命题的序号是②③④． 15．【答案】 【解析】在椭圆 中， ， ， ． ∵ 的内切圆的周长为 ，∴ 内切圆的半径为 ． 由椭圆的定义得 的周长为: 2 4x < 2 2x− < < 2x < 2 4x < 0ab > 2b a a b + ≥ ( )22 2 22 0a bb a a b ab a b ab ab −+ −+ − = = > 0ab > 0ab > 2b a a b + > 1 0a < 2 3 2 3 1 0S S a a q− = = < 3 2S S< 3 2S S< 2 3 2 3 1 0S S a a q− = = < 1 0a < 1 0a < 3 2S S< 1x = − 1 1 1 2 2x x + = − − = − ≤ x∃ ∈R 2 1 2x x+ ≤ ( )21 0x∴ − ≤ 1x = 0 0≤ 0x > 0y > ( )2 2 2 , 01 12 2 a b a b ab a b a b + + > + ≥ ≥ ≥ 2 2 2 2 1 12 x y xy x y x y +∴ =+ + ≥ 5m = − 2 5 4 0x x∴ − + < ( )( )4 1 0x x− − < 1 4x∴ < < 10 3 2 2 125 16 x y+ = 5a = 4b = 3c = 2ABF△ 2π 2ABF△ 1r = 2ABF△ ， 又 ， 且 ，∴ ，解得 ． 16．【答案】 【解析】∵平面 SAB⊥平面 SAD，平面 SAB∩平面 SAD=SA，侧面 SAB 是边长为 的等边三角形，设 AB 的中点为 E，SA 的中点为 F， 则 BF⊥SA，∴BF⊥平面 SAD，∴BF⊥AD，底面 ABCD 是矩形， ∴AD⊥平面 SAB，SE⊂平面 SAB， ∴AD⊥SE，又 SE⊥AB，AB∩AD=A， ∴SE⊥底面 ABCD，作图如下： ∵SAB 是边长为 的等边三角形， ∴ ． 又底面 ABCD 是矩形，且 BC=4， ∴矩形 ABCD 的对角线长为 ， ∴矩形 ABCD 的外接圆的半径为 ． 设该四棱锥外接球的球心为 O，半径为 R，O 到底面的距离为 h， 则 r2+h2=R2，即 7+h2=R2，又 R2=22+（SE−h）2=4+（3−h）2， ∴7+h2=4+（3−h）2，∴h=1．∴R2=7+h2=8， ∴该四棱锥外接球的表面积 ． 三、解答题：解答应写出文字说明、证明过程或演算步骤． 17．【答案】（1） ；（2） ． ( ) ( )12 2 1 22AB BF AF AF AF BF BF+ + = + + + 4 20a= = ( ) 2 2 2 1 1 1 20 102 2ABFS r AB BF AF= + + = × × =△ 2 1 2 1 2 1 2 1 32ABFS F F y y y y= − = −△ 1 23 10y y− = 1 2 10 3y y− = 32π 2 3 2 3 32 3sin 60 2 3 32SE = ° = × = ( )224 2 3 2 7+ = 7r = 24π 32πS R= = { | 2 3 7 10}x x x< <≤ 或 ≤ [ )7,+∞ 【解析】（1） ， ， ． ， ． （2） 是 的充分不必要条件，则 ，所以 ，即 的取值范围是 18．【答案】（1） ；（2） ． 【解析】（1）由 及正弦定理得： ， 即 ， ，又 为三角形的内角， ． （2）由余弦定理 ，得 ． 19．【答案】（1） ；（2） ． 【解析】（1）当 时， ，当 时， ， 当 时， 不满足上式，故 ； （2） ， ， 令 ······①， ······②， ①－②得： ， ， ． 20．【答案】（1）如果只安排生产书桌，最多可生产 张书桌，获得利润 { | 3 7}A x x= < < { | 2 10}B x x= < < { | }C x x a= < { | 3 7}A x x x=R ≤ 或 ≥ ( ) { | 2 3 7 10}A B x x x= < = = + ×   2m = ( )0,1,2P PF PDλ=  ( )0,0,2AP = ( )3, 1, 2PD = − − ( )3 , ,2 2AF AP PF λ λ λ= + = − −   PEC ( ), ,m x y z= 3 1, ,22 2EP  =      ( )0, 2, 2PC = − − 3 1 2 02 2 2 2 0 x y z y z  + + = − − = ( )3, 1,1m = − − 0m AF⋅ = 3 2 2 0λ λ λ− + + − = 1 2 λ = F PD PEA ( )1= 3, 3,0n − PED ( )2 = 3,9, 3n − 1 2 3 27 4cos , 313112 93 n n −< >= = − ×   D PE A− − D PE A− − ．4 3131