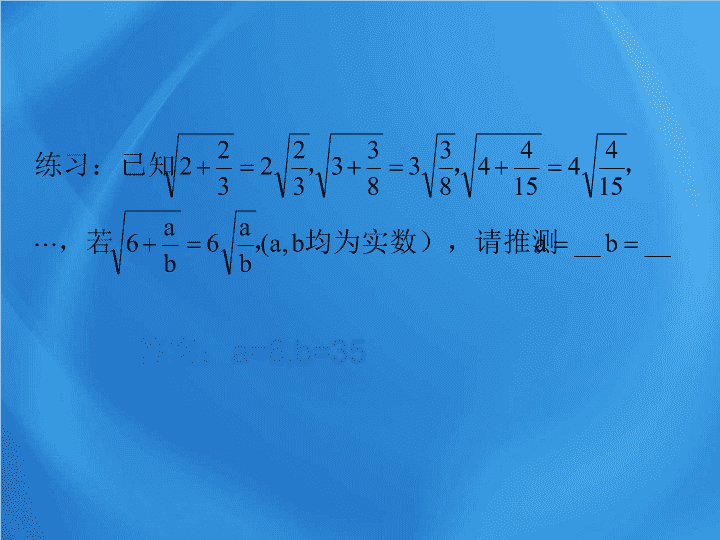- 1.87 MB
- 2021-06-23 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
合情推理(二)
——
类比推理
知识回顾:
由某类事物的
部分
对象具有某些特征
,
推出该类事物的
全部
对象都具有这些特征的推理
,
或者由
个别
事实概栝出
一般
结论的推理
,
称为
归纳推理
.(
简称归纳
)
2
、归纳推理的一般模式
:
S
1
具有
P,
S
2
具有
P,
……
S
n
具有
P,
(S
1
,S
2
,
…
,S
n
是
A
类事物的对象)
所以
A
类事物具有
P
1
、什么是归纳推理?
答案:
a=6,b=35
从一个传说说起:春秋时代鲁国的公输班(后人称鲁班,被认为是木匠业的祖师)一次去林中砍树时被一株齿形的茅草割破了手,这桩倒霉事却使他发明了锯子
.
他的思路是这样的:
茅草是齿形的
;
茅草能割破手
.
我需要一种能割断木头的工具;
它也可以是齿形的
.
这个推理过程是归纳推理吗?
二、情景引入:
可能有生命存在
有生命存在
温度适合生物的生存
一年中有四季的变更
有大气层
大部分时间的温度适合地球上某些已知生物的生存
一年中有四季的变更
有大气层
行星、围绕太阳运行、绕轴自转
行星、围绕太阳运行、绕轴自转
火星
地球
火星上是否存在生命
火星
与
地球
类比的思维过程:
火星
地球
存在类似特征
地球上有生命存在
猜测火星上也可能有生命存在
这种由两个(两类)对象之间在某些方面的相似或相同,推演出他们在其他方面也相似或相同;或其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为
类比推理
(简称
类比
).
简言之,
类比推理是由特殊到特殊的推理
.
类比推理举例
探究
1
:
类比圆的特征,说说球的相关特征,并说明推理的过程。
试将平面上的圆与空间的球进行类比
.
圆的定义
:平面内到一个定点的距离等于定长的点的集合
球的定义:
空间中到一个定点的距离等于定长的点的集合
圆
弦
直径周长
面积
球
截面圆
大圆
表面积
体积
.
.
圆的概念和性质
球的概念和性质
与圆心距离相等的两弦相等
与圆心距离不相等的两弦不相等
,
距圆心较近的弦较长
以点
(x
0
,y
0
)
为圆心
, r
为半径的圆的方程为
(x-x
0
)
2
+(y-y
0
)
2
= r
2
圆心与弦(非直径)中点的连线垂直于弦
球心与不过球心的截面
(
圆面
)
的圆点的连线垂直于截面
与球心距离相等的两截面面积相等
与球心距离不相等的两截面面积不相等
,
距球心较近的面积较大
以点
(x
0
,y
0
,z
0
)
为球心
, r
为半径的球的方程为
(x-x
0
)
2
+(y-y
0
)
2
+(z-z
0
)
2
= r
2
利用圆的性质类比得出求的性质
球的体积
球的表面积
圆的周长
圆的
面积
试根据等式的性质猜想不等式的性质。
等式的性质:
(1) a=b
a+c=b+c;
(2) a=b
ac=bc;
(3)
a=b
a
2
=b
2
;
等等。
猜想不等式的性质:
(1) a
>
b
a+c
>
b+c;
(2) a
>
b
ac
>
bc;
(3)
a
>
b
a
2
>
b
2
;
等等。
问:这样猜想出的结论是否一定正确?
让我们一起来类比推理
类比推理的结论不一定成立
.
我们已经学习过
“等差数列”
与
“等比数列”
.
你是否想过
“等和数列”、“等积数列”
?
从第二项起,每一项与其前一项的
差
等于一个常数的数列是
等差数列
.
类推
从第二项起,每一项与其前一项的
和
等于一个常数的数列是
等和数列
.
类比某些熟悉的概念,产生的类比推理型试题;在求解时可以借助原概念所涉及的基本方法与基本思路。
例
1.
等和数列的定义是:若数列
{
a
n
}
从第二项起,以后每一项与前一项的和都是同一常数,则此数列叫做等和数列,这个常数叫做等和数列的公和;如果数列
{
a
n
}
是等和数列,且
a
1
=1
,
a
2
=2
,写出数列
{
a
n
}
的一个通项公式为
;
分析:
由定义知公和为
3
,且
那么
类比推理
1----
类比概念
类比推理的几个特点
;
1.
类比是从人们已经掌握了的事物的属性
,
推测正在研究的事物的属性
,
是以旧有的认识为基础
,
类比出新的结果
.
2.
类比是从一种事物的特殊属性推测另一种事物的特殊属性
.
3.
类比的结果是猜测性的不一定可靠
,
单它却有发现的功能
.
3
、进行类比推理的
步骤
:
(1)
找出两类对象之间可以确切表述的相似特征;
(2)
用一类对象的已知特征去猜测另一类对象的特征,从而得出一个猜想;
(3)
检验这个猜想
.
4
、类比推理的一般模式
:
所以
B
类事物可能具有性质
d
’
.
A
类事物具有性质
a,b,c,d,
B
类事物具有性质
a
’
,b
’
,c
’
,
(a,b,c
与
a
’
,b
’
,c
’
相似或相同)
观察、比较
联想、类推
猜想新结论
运用类比法的关键是:
寻找一个合适的
类比对象
基本原则是:要根据当前问题的需要,选择
适当的类比对象
。
思考:平面几何中的哪一类图形可以作为四面体的类比对象
构成几何体的元素数目:三角形 四面体
平面图形(二维)
立体图形(三维)
点
点或线
线
线或面
平面直角坐标系
空间直角坐标系
从初中到高中我们学过的定理很多,这些定理是产生类比型问题的“沃土”。请看:
例
2.
在平面几何里有勾股定理:
“
设的两边互相垂直,则。
”
拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积之间的关系,可以得出的正确结论是:
“
设三棱锥的三侧面两两垂直,则
。
”
(
03
年全国卷第
15
题)
分析:在平面上是线的关系,在空间呢?假若是面的关系,
类比一下:
直角顶点所对的边的平方是另外两边的平方和,而直角顶点所对的面会有什么关系呢?
大胆一点猜测:
类比推理
2----
类比定理
类比推理
2----
类比定理
事实上,如图作
AE
⊥
CD
于
E,
连
BE
,
则
BE
⊥
CD
平面图形与空间图形的类比关系如下:
平面图形
空间图形
点
线
线(线段长度)
面(面积)
面(封闭图形)(面积)
体(几何体)(体积)
类比推理
2----
类比定理
1.
如图,在平行四边形 中,有
那么,在平行六面体 中,有
练习:
从一个特殊式子的性质、一个特殊图形的性质入手,产生的类比推理型问题;求解时要认真分析两者之间的联系与区别,深入思考两者的转化过程是求解的关键。
例
3.
我们知道:圆的任意一弦(非直径)的中点和圆心连线与该弦垂直;那么,若椭圆
b
2
x
2
+
a
2
y
2
=
a
2
b
2
的一弦中点与原点连线及弦所在直线的斜率均存在,你能得到什么结论?请予以证明。
类比推理
3----
类比性质
类比推理
3----
类比性质
分析:
假若弦的斜率与弦的中点和圆心连线的斜率都存在,由于两线垂直,我们知道斜率之积为-
1
;对于方程 ,若
a
=
b
,则方程即为圆
的方程,由此可以猜测两斜率之积为 或 ;
证明:
设弦
AB
的两端点的坐标分别为
A
(
x
1
,
y
1
)
,
B
(
x
2
,
y
2
)
,
中点为
P
,则
例
4.
在平面上
,
设
h
a
,h
b
,h
c
是三角形
ABC
三条边上的高
.P
为三角形内任一点
,P
到相应三边的距离分别为
p
a
,p
b
,p
c
,
我们可以得到结论
:
试通过类比
,
写出在空间中的类似结论
.
类比推理
3----
类比性质
类比推理
3----
类比性质
平面上
空间中
图
形
结论
证
法
A
B
C
P
p
a
p
b
p
c
A
B
C
D
P
类比推理
3----
类比性质
证
法
类比推理
3----
类比性质
练习
2
(
2004
广东,
15
)
由图
(1)
有面积关系
:
则由图
(2)
有体积关系
:
图
(1)
图
(2)
有一些处理问题的方法,具有类比性,结合这些方法产生的问题,在求解时,要注意知识的迁移。
例
5.
若点
P
是正四面体 的面
BCD
上一点,且
P
到另三个面的距离分别为
h
1
,
h
2
,
h
3
,该正四面体的高为
h
,则( )
分析:
由点
P
是正三角形
ABC
的边
BC
上一点,且到另两边的距离分别为
h
1
和
h
2
,正三角形
ABC
的高为
h
,由面积相等很快可以得到
h
=
h
1
+
h
2
;于是,类比方法,平面上用面积,空间中用体积,立即可得答案为
B
类比推理
4----
类比方法
分析:面积法
例
6
☞
类比推理
5----
类比方法
A
B
C
D
O
O
类比推理
5----
类比方法
数列知识是类比的沃土
---
例
7.
数列知识是类比的沃土
---
练习
3.
练习
.
数列知识是类比的沃土
---
练习
4.
观察下面图形规律,在其右下角的空格内画上合适的图形为( )
A. ■ B. △ C. □ D. ○
□
●
▲
▲
■
○
●
△
练习
5.
最后提醒
----
类比陷阱
类比推理是一种很好、很重要的推理,为使这种推理更严谨、更完美,有时也会故意设计一些让你“误入歧途”的类比推理型陷阱题。
例
8.
平面几何中有
“
一个角的两边分别垂直于另一个角的两边则两角相等或互补
”
;在立几
“
当一个二面角的两个半平面分别垂直于另一个二面角的两个半平面时
”
,两二面角( )
A.
互补
B.
相等
C.
互补或相等
D.
此两二面角的关系不定
分析:
平几中的这个结论有很大的误导性,建立在这个结论的基础上,很多同学也许会不知不觉“上当”误选答案(
C
);
其实,正确答案为(
D
),作一个图形就可以发现结论。
类比推理
类比推理
以
旧
的知识为基础
,
推测
新
的结果,具有
发现的功能
由
特殊到特殊
的推理
类比推理的结论
不一定成立
注意
类比推理
由
特殊到特殊
的推理
;
以旧的知识为基础
,
推测
新
的结果;
结论不一定成立
.
归纳推理
由部分到整体、
特殊到一般
的推理
;
以观察分析为基础
,
推测
新
的结论
;
具有
发现
的功能
;
结论不一定成立
.
具有
发现
的功能
;
没有大胆猜测就没有伟大发明 牛顿
小结
☞
归纳推理和类比推理的过程
从具体问题出发
观察、分析、比较、联想
归纳、类比
提出猜想
通俗地说,合情推理是指
“合乎情理”
的推理
.
合情推理
归纳推理
类比推理
几何中常见的类比对象
三角形
四面体
(各面均为
三角形
)
四边形
六面体
(各面均为
四边形
)
圆
球
代数中常见的类比对象
数
向量
方程
函数
不等式
交集,并集,补集
或,且,非运算
无限
有限
善于观察勤于思考敢于猜想的人
常常会冒出创造的灵感火花
再 见