高中数学：新人教A版选修1-1 3_1变化率与导数（同步练习） 7页

人教新课标版（A）选修1-1 3.1 变化率与导数同步练习题 ‎【基础演练】‎ 题型一：变化率问题与导数概念 ‎ 一般地，我们称为平均变化率，如果时，存在，称此极限值为函数在处的导数，记作，请根据以上知识解决以下1~5题。‎ ‎ 1. 一质点运动的方程为，则在一段时间内相应的平均速度为 ‎ A. B. C. D. ‎ ‎ 2. 将半径为R的球加热，若球的半径增加△R，则球的体积增加△y约等于 ‎ A. B. C. D. ‎ ‎ 3. 已知函数的图象上一点（1，2）及邻近一点，则等于 ‎ A. 2 B. 2x C. 2+△x D. 2+△‎ ‎ 4. 自变量变到时，函数值的增量与相应自变量的增量之比是函数 ‎ A. 在区间上的平均变化率 B. 在处的变化率 C. 在处的变化量 D. 在区间上的导数 ‎ 5.若函数在处的导数为A，求。‎ 题型二：导数的物理意义 ‎ 在物体的运动规律中，如果，那么物体的瞬时速度；如果，那么物体的加速度，请根据以上知识解决以下6~7题。‎ ‎ 6. 若一物体运动方程如下：‎ ‎ ‎ ‎ 求物体在或时的速度。‎ ‎ 7. 质点M按规律做直线运动，则质点的加速度a=___________。‎ 题型三：导数的几何意义 ‎ 导数的几何意义：函数在处的导数，即曲线在点P（）处切线的斜率为，相应的切线方程是，请根据以上知识解决以下8~9题。‎ ‎ 8. 下面说法正确的是 ‎ A. 若不存在，则曲线在点（，）处没有切线 B. 若曲线在点（）处有切线，则必存在 C. 若不存在，则曲线在点（）处的切线斜率不存在 D. 若曲线在点（）处没有切线，则可能存在 ‎ 9. 已知曲线C：。‎ ‎ （1）求曲线C上横坐标为1的点处的切线方程 ‎ （2）第（1）小题中的切线与曲线C是否还有其他的公共点？‎ ‎【互运探究】‎ ‎［学科内综合］‎ ‎ 10. 设，在处可导是在（a，b）内可导的 ‎ A. 充分非必要条件 B. 必要而非充分条件 C. 充要条件 D. 既非充分又非必要条件 ‎ 11. 如图‎3-1-1‎表示物体运动的路程随时间变化的函数的图象，试根据图象，描述、比较曲线在、、附近的变化情况，并求出时的切线的方程。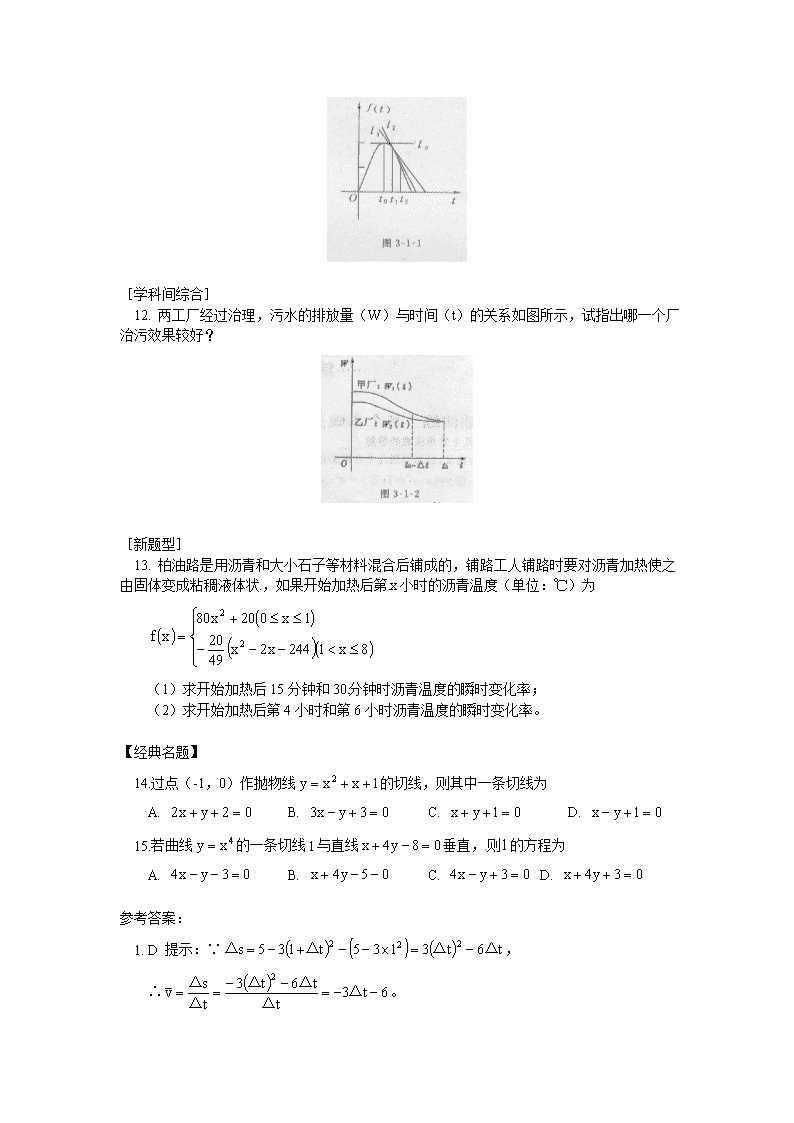‎ ‎［学科间综合］‎ ‎ 12. 两工厂经过治理，污水的排放量（W）与时间（t）的关系如图所示，试指出哪一个厂治污效果较好？‎ ‎［新题型］‎ ‎ 13. 柏油路是用沥青和大小石子等材料混合后铺成的，铺路工人铺路时要对沥青加热使之由固体变成粘稠液体状，如果开始加热后第x小时的沥青温度（单位：℃）为 ‎ ‎ ‎ （1）求开始加热后15分钟和30分钟时沥青温度的瞬时变化率；‎ ‎ （2）求开始加热后第4小时和第6小时沥青温度的瞬时变化率。‎ ‎【经典名题】‎ ‎ 14.过点（-1，0）作抛物线的切线，则其中一条切线为 ‎ A. B. C. D. ‎ ‎ 15.若曲线的一条切线l与直线垂直，则的方程为 ‎ A. B. C. D. ‎ 参考答案：‎ ‎ 1. D 提示：∵，‎ ‎∴。‎ ‎ 2. B 提示：∵，‎ ‎∴‎ ‎，‎ ‎∵R是一个很小的量，‎ ‎∴和（△R）非常小，‎ ‎∴。‎ ‎ 3. C 4. A ‎ 5. 解：∵，‎ ‎∴（令替换），‎ ‎∴‎ ‎（当时，）‎ ‎。‎ ‎ 6. 解：当时，，‎ ‎ ‎ ‎，‎ ‎∴。‎ 当时，， ‎ ‎，‎ ‎∴。‎ ‎∴物体在和时的瞬时速度分别是6和0。‎ ‎ 7. 4 提示：。‎ ‎ ∴。‎ ‎ 8. C ‎ 9. 解：（1）将代入曲线C的方程，得，‎ ‎ ∴切点的坐标为（1，1）。‎ ‎∵‎ ‎，‎ ‎∴，‎ ‎∴过点（1，1）的切线的方程为 ‎，‎ 即。‎ ‎（2）由，得 整理得，‎ 解得或。‎ 从而获得切线与曲线的公共点为（1，1）和（-2，-8）。‎ 说明切线与曲线C的公共点除去切点外，还有一个公共点（-2，-8）‎ 提示：本例回答了一个问题：直线与曲线相切是否一定只有一个公共点。‎ ‎ 10. B ‎ 11. 解：用曲线在、、处的切线刻画曲线在、、附近的变化情况。‎ ‎ （1）当时，曲线在处的切线平行于x轴，所以在附近曲线比较平坦，几乎没有升降。‎ ‎ （2）当时，曲线在处的切线的斜率，所以在附近曲线下降，即函数在附近单调递减。‎ ‎（3）当时，曲线在处的切线的斜率，所以在附近曲线下降，即函数在附近也单调递减。由图象可以看出，直线的倾斜程度小于直线的倾斜程度，说明曲线在附近比在附近下降得缓慢。‎ ‎（4）当时，。‎ 在是的切线的斜率 ‎。‎ 所以切线的方程为。‎ 即。‎ 提示：导数的几何意义是曲线的切线斜率，反过来，在曲线上取定一点作曲线的切线时，能根据切线判定斜率的符号即导数的符号，进而根据符号确定在该点附近曲线的升降情况（或函数的增减情况），同时可以根据几点处的切线倾斜程度的大小，判断曲线升降的快慢程度。‎ ‎ 12. 解：在处，虽然，但，所以说，在单位时间里，企业甲比企业乙的平均治污率大，因此企业甲比企业乙略好一些。‎ ‎ 13. 解：（1）∵时，‎ ‎，‎ ‎15分钟=0.25小时，‎ ‎30分钟=0.5小时，‎ ‎∴沥青温度在15分钟和30分钟时的瞬时变化率就是函数在处和处的导数和，‎ ‎∵‎ ‎，‎ ‎∴，‎ ‎∵同理可得 ‎。‎ ‎（2）当时，‎ ‎，‎ 当时， ‎ ‎，‎ ‎∴，同理当时，，‎ ‎∴。‎ 提示：函数在某一点处的瞬时变化率就是在处的导数，物体在某一时刻处的瞬时的速度就是相应运动方程在处的导数。‎ ‎ 14. C ‎ ‎15. A ‎ ‎ ‎ ‎