2019高三数学理北师大版一轮单元评估检测7　第7章　立体几何 12页

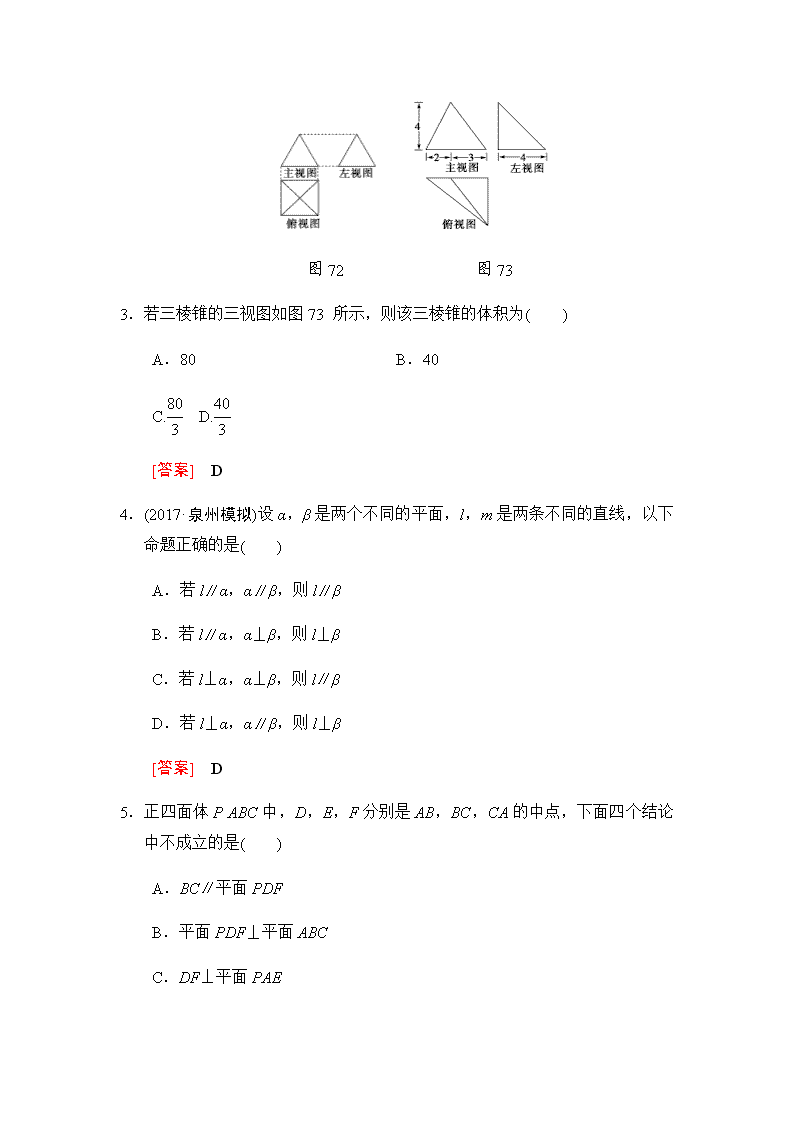
单元评估检测(七)　第7章　立体几何 ‎(120分钟　150分)‎ ‎(对应学生用书第294页)‎ 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．中央电视台正大综艺以前有一个非常受欢迎的娱乐节目：墙来了！选手需按墙上的空洞造型摆出相同姿势，才能穿墙而过，否则会被墙推入水池．类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞(如图71)，则该几何体为(　　)‎ 图71‎ ‎[答案]　A ‎2．(2018·衡阳模拟)如果一个几何体的三视图如图72所示，主视图与左视图是边长为2的正三角形，俯视图轮廓为正方形(单位：cm)，则此几何体的侧面积是(　　)‎ ‎【导学号：79140426】‎ A．2 cm2 B．4 cm2‎ C．8 cm2 D．14 cm2‎ ‎[答案]　C ‎　　‎ 图72　　　　　　　　图73‎ ‎3．若三棱锥的三视图如图73所示，则该三棱锥的体积为(　　)‎ A．80 B．40 ‎ C. D. ‎[答案]　D ‎4．(2017·泉州模拟)设α，β是两个不同的平面，l，m是两条不同的直线，以下命题正确的是(　　)‎ A．若l∥α，α∥β，则l∥β B．若l∥α，α⊥β，则l⊥β C．若l⊥α，α⊥β，则l∥β D．若l⊥α，α∥β，则l⊥β ‎[答案]　D ‎5．正四面体PABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是(　　)‎ A．BC∥平面PDF B．平面PDF⊥平面ABC C．DF⊥平面PAE D．平面PAE⊥平面ABC ‎[答案]　B ‎6．在正三棱柱ABCA1B1C1中，若AB＝2，AA1＝1，则点A到平面A1BC的距离为(　　)‎ A. B. C. D. ‎[答案]　B ‎7．如图74，四面体ABCD中，AB＝DC＝1，BD＝，AD＝BC＝，二面角ABDC的平面角的大小为60°，E，F分别是BC，AD的中点，则异面直线EF与AC所成的角的余弦值是(　　)‎ 图74‎ A. B. C. D. ‎[答案]　B ‎8．如图75，在正方体ABCDA1B1C1D1中，下列结论错误的是(　　)‎ 图75‎ A．直线BD1与直线B1C所成的角为 B．直线B1C与直线A1C1所成的角为 C．线段BD1在平面AB1C内的射影是一个点 D．线段BD1恰被平面AB1C平分 ‎[答案]　D ‎9．如图76，在四棱锥PABCD中，侧面PAD为正三角形，底面ABCD是边长为2的正方形，侧面PAD⊥底面ABCD，M为底面ABCD内的一个动点，且满足MP＝MC，则点M的正方形ABCD内的轨迹的长度为(　　)‎ 图76‎ A. B．2 ‎ C．π D. ‎[答案]　A ‎10．棱长为4的正四面体内切一球，然后在正四面体和该球形成的空隙处各放入一个小球，则这些小球的最大半径为(　　) ‎ ‎【导学号：79140427】‎ A. B. C. D. ‎[答案]　B ‎11．(2017·南阳模拟)如图77是一个由两个半圆锥与一个长方体组合而成的几何体的三视图，则该几何体的体积为(　　)‎ 图77‎ A．6＋ B．8＋ C．4＋ D．4＋ ‎[答案]　C ‎12．下列命题中错误的是(　　)‎ A．如果α⊥β，那么α内一定有直线平行于平面β B．如果α⊥β，那么α内所有直线都垂直于平面β C．如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β D．如果α⊥γ，β⊥γ，α∩β＝l，那么l⊥γ ‎[答案]　B 二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上)‎ ‎13．半径为的球的体积与一个长、宽分别为6,4的长方体的体积相等，则长方体的表面积为________．‎ ‎[答案]　88‎ ‎14．(2017·运城模拟)如图78，三棱柱ABCA1B1C1的体积为V1，四棱锥ABCC1B1的体积为V2，则＝________.‎ 图78‎ ‎[答案]　 ‎15．如图79，矩形ABCD中，AB＝2AD，E为AB的中点，将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点，则在△ADE翻折过程中，下面四个命题中正确的是________．(填序号)‎ 图79‎ ‎①BM是定值；‎ ‎②点M在某个球面上运动；‎ ‎③存在某个位置，使DE⊥A1C；‎ ‎④存在某个位置，使MB∥平面A1DE.‎ ‎[答案]　①②④‎ ‎16．已知向量a＝(0，－1,1)，b＝(4,1,0)，|λa＋b|＝且λ＞0，则λ＝________. ‎ ‎【导学号：79140428】‎ ‎[答案]　3‎ 三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17．(本小题满分10分)(2018·南昌模拟)如图710所示，设计一个四棱锥形冷水塔塔顶，四棱锥的底面是正方形，侧面是全等的等腰三角形，已知底面边长为2 m，高为 m，则制造这个塔顶需要多少面积的铁板？‎ 图710‎ ‎[解]　制造这个塔顶需要8 m2的铁板．‎ ‎18．(本小题满分12分)(2017·长沙模拟)如图711，在三棱锥PABC中，∠PAB＝∠PAC＝∠ACB＝90°.‎ 图711‎ ‎(1)求证：平面PBC⊥平面PAC；‎ ‎(2)若PA＝1，AB＝2，BC＝，在直线AC上是否存在一点D，使得直线BD与平面PBC所成角为30°？若存在，求出CD的长；若不存在，说明理由．‎ ‎[解]　(1)略　(2)存在，CD＝.‎ ‎19．(本小题满分12分)如图712，在三棱柱ABCA1B1C1中，侧面ABB1A1⊥底面ABC，CA＝CB，D，E，F分别为AB，A1D，A1C的中点，点G在AA1上，且A1D⊥EG.‎ 图712‎ ‎(1)求证：CD∥平面EFG；‎ ‎(2)求证：A1D⊥平面EFG.‎ ‎[解]　略 ‎20．(本小题满分12分) (2017·江西五市三联)如图713，在四棱锥PABCD中，AD∥BC，AB⊥AD，AB＝AD＝AP＝2BC＝2，M是棱PD上的一点，＝λ(0＜λ＜1)．‎ 图713‎ ‎(1)若λ＝，求证：PB∥平面MAC；‎ ‎(2)若平面PAB⊥平面ABCD，平面PAD⊥平面ABCD，二面角DACM的余弦值为，求λ的值．‎ ‎[解]　(1)略　(2).‎ ‎21．(本小题满分12分)(2017·新乡模拟)如图714(1)，在三角形PCD中，AB为其中位线，且2BD＝PC，若沿AB将三角形PAB折起，使∠PAD＝‎ θ，构成四棱锥PABCD，且＝＝2，如图714(2)．‎ 图714‎ ‎(1)求证：平面BEF⊥平面PAB；‎ ‎(2)当异面直线BF与PA所成的角为60°时，求折起的角度θ. ‎ ‎【导学号：79140429】‎ ‎[解]　(1)因为2BD＝PC，所以∠PDC＝90°，‎ 因为AB∥CD，且＝＝2，所以E为CD的中点，F为PC的中点，CD＝2AB，所以AB∥DE且AB＝DE，所以四边形ABED为平行四边形，所以BE∥AD，BE＝AD，‎ 因为BA⊥PA，BA⊥AD，且PA∩AD＝A，所以BA⊥平面PAD，‎ 因为AB∥CD，所以CD⊥平面PAD，又因为PD平面PAD，AD平面PAD，‎ 所以CD⊥PD且CD⊥AD，又因为在平面PCD中，EF∥PD(三角形的中位线)，于是CD⊥FE.‎ 因为在平面ABCD中，BE∥AD，‎ 于是CD⊥BE，‎ 因为FE∩BE＝E，FE平面BEF，BE平面BEF，所以CD⊥平面BEF，‎ 又因为CD∥AB，AB在平面PAB内，所以平面BEF⊥平面PAB.‎ ‎(2)因为∠PAD＝θ，取PD的中点G，连接FG，AG，所以FG∥CD，FG＝CD，又AB∥CD，AB＝CD，‎ 所以FG∥AB，FG＝AB，从而四边形ABFG为平行四边形，所以BF∥AG，所以BF与PA所成的角即为AG与PA所成的角，即∠PAG＝60°，因为PA＝AD，G为PD中点，所以AG⊥PD，∠APG＝30°，所以∠PDA＝30°，所以∠PAD＝180°－30°－30°＝120°.故折起的角度为120°.‎ ‎22．(本小题满分12分)(2018·周口模拟)如图715，正方形ADEF与梯形ABCD所在平面互相垂直，AD⊥CD，AB∥CD，AB＝AD＝CD＝2，点M在线段EC上且不与E，C重合．‎ 图715‎ ‎(1)当点M是EC中点时，求证：BM∥平面ADEF；‎ ‎(2)当平面BDM与平面ABF所成锐二面角的余弦值为时，求三棱锥MBDE的体积．‎ ‎[解]　(1)取ED的中点N，‎ 连接MN，AN，‎ 又因为点M是EC的中点，‎ 所以MN∥DC，‎ MN＝DC，‎ 而AB∥DC，AB＝DC，‎ 所以MNAB，‎ 所以四边形ABMN是平行四边形，‎ 所以BM∥AN，‎ 而BM⃘平面ADEF，AN平面ADEF，‎ 所以BM∥平面ADEF.‎ ‎(2)取CD的中点O，过点O作OP⊥DM，连接BP，BO，‎ 因为AB∥CD，AB＝CD＝2，‎ 所以四边形ABOD是平行四边形，‎ 因为AD⊥DC，‎ 所以四边形ABOD是矩形，‎ 所以BO⊥CD，‎ 因为正方形ADEF与梯形ABCD所在平面互相垂直，ED⊥AD，‎ 所以ED⊥平面ADCB，‎ 所以平面CDE⊥平面ADCB，‎ 所以BO⊥平面CDE，所以BP⊥DM，‎ 所以∠OPB是平面BDM与平面DCE(即平面ABF)所成锐二面角，‎ 因为cos∠OPB＝，所以sin∠OPB＝，‎ 所以＝，解得BP＝.‎ 所以OP＝BPcos∠OPB＝，所以sin∠MDC＝＝，‎ 而sin∠ECD＝＝，‎ 所以∠MDC＝∠ECD，‎ 所以DM＝MC，同理DM＝EM，所以M为EC的中点，‎ 所以S△DEM＝S△CDE＝2，‎ 因为AD⊥CD，AD⊥DE，‎ 且DE与CD相交于点D，‎ 所以AD⊥平面CDE，因为AB∥CD，‎ 所以三棱锥BDME的高＝AD＝2，‎ 所以VMBDE＝VBDEM＝S△DEM·AD＝.‎