专题20 综合训练3（第02期）-2018年高考数学（文）备考之百强校小题精练系列 5页

‎1．设集合，则（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】由题意得， ，则 ，故选B．‎ ‎2．为虚数单位，已知复数满足，则（ ）‎ A． B． C． D． ‎ ‎【答案】C ‎【解析】由题意得，设，则， ，故选C．‎ ‎3．下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目，则这些车辆数的中位数和众数分别是（ ）‎ A． 230．5，220 B． 231．5，232 C． 231，231 D． 232，231‎ ‎【答案】C ‎4．已知向量满足，向量与的夹角为60°，则（ ）‎ A． B． 19 C． D． 7‎ ‎【答案】C ‎【解析】由题意得， ，则选C．‎ ‎5．已知，则的值为 （ ）‎ A． B． 1 C． D． ‎ ‎【答案】A ‎【解析】由题意得， ，则 ，故选A．‎ ‎6．四个数的大小顺序是 （ ）‎ A． B． ‎ C． D． ‎ ‎【答案】D ‎【解析】由题意得， ，故选D．‎ ‎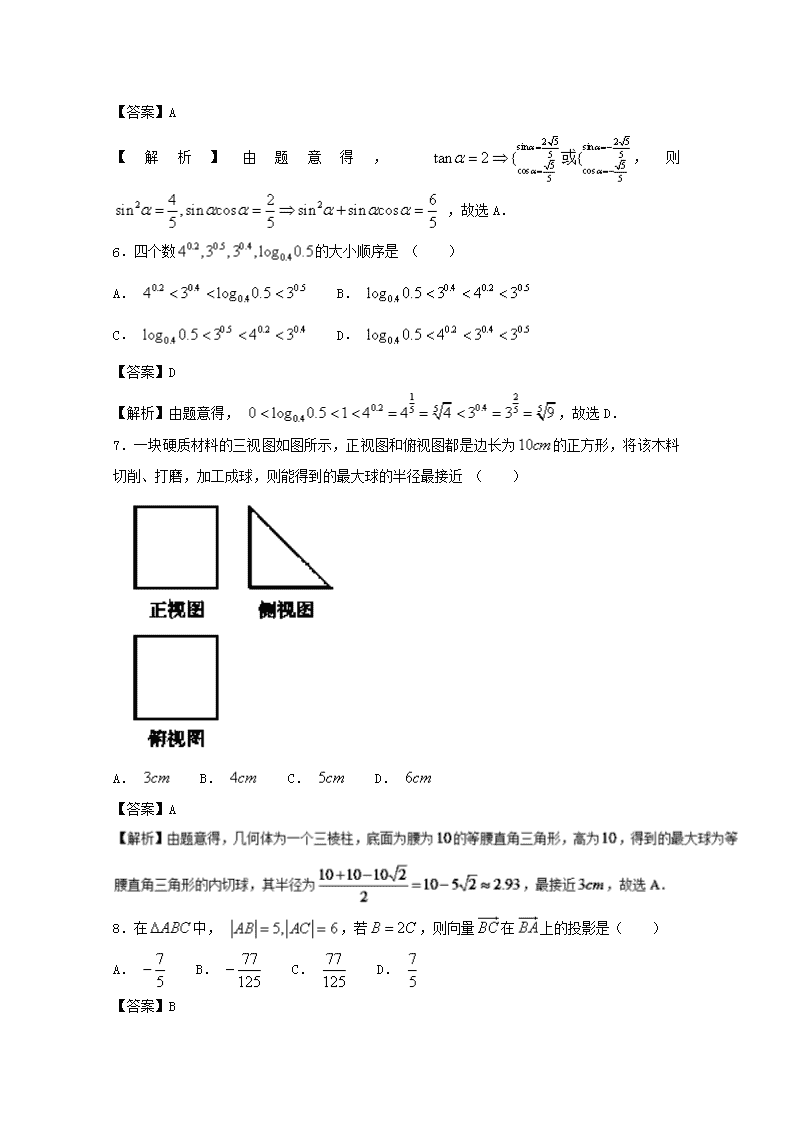7．一块硬质材料的三视图如图所示，正视图和俯视图都是边长为的正方形，将该木料切削、打磨，加工成球，则能得到的最大球的半径最接近 （ ）‎ A． B． C． D． ‎ ‎【答案】A ‎8．在中， ，若，则向量在上的投影是（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】由正弦定理得， ,由余弦定理得， ,则 ，故选B．‎ ‎9．已知双曲线的右顶点为，抛物线的焦点为．若在的渐近线上存在点，使得，则的离心率的取值范围是 （ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【点睛】本题主要考查了双曲线的基本性质的应用，抛物线基本性质的应用，向量数量积坐标运算以及一元二次方程根的判别式的运用，属于中档题，首先可画一张草图，分析其中的几何关系，然后将系用代数形式表示出来，即可得到一个一元二次方程，若要使得一元二次方程有实数解， ，水到渠成，即可得到答案，因此将几何关系转化成方程是解题的关键．‎ ‎10．已知实数满足，则的最大值是__________．‎ ‎【答案】‎ ‎【解析】由约束条件可作如图所示的可行域，两直线的交点,则当过原点的直线过点时，斜率最大，即的最大值为．‎ ‎11．将函数的图象向左平移个单位，再将所得图象上各点的横坐标缩为原来的，纵坐标不变，便得到函数的图象，则解析式为__________．‎ ‎【答案】‎ ‎12．若直线（都是正实数）与圆相交于两点，当（是坐标原点）的面积最大时， 的最大值为__________．‎ ‎【答案】2‎ ‎【解析】根据题意画出图形，如图所示：‎ 由的面积为可得， 为直角三角形， ,则点到直线 的距离为，即，那么只有当且仅当时， 取最大值．‎