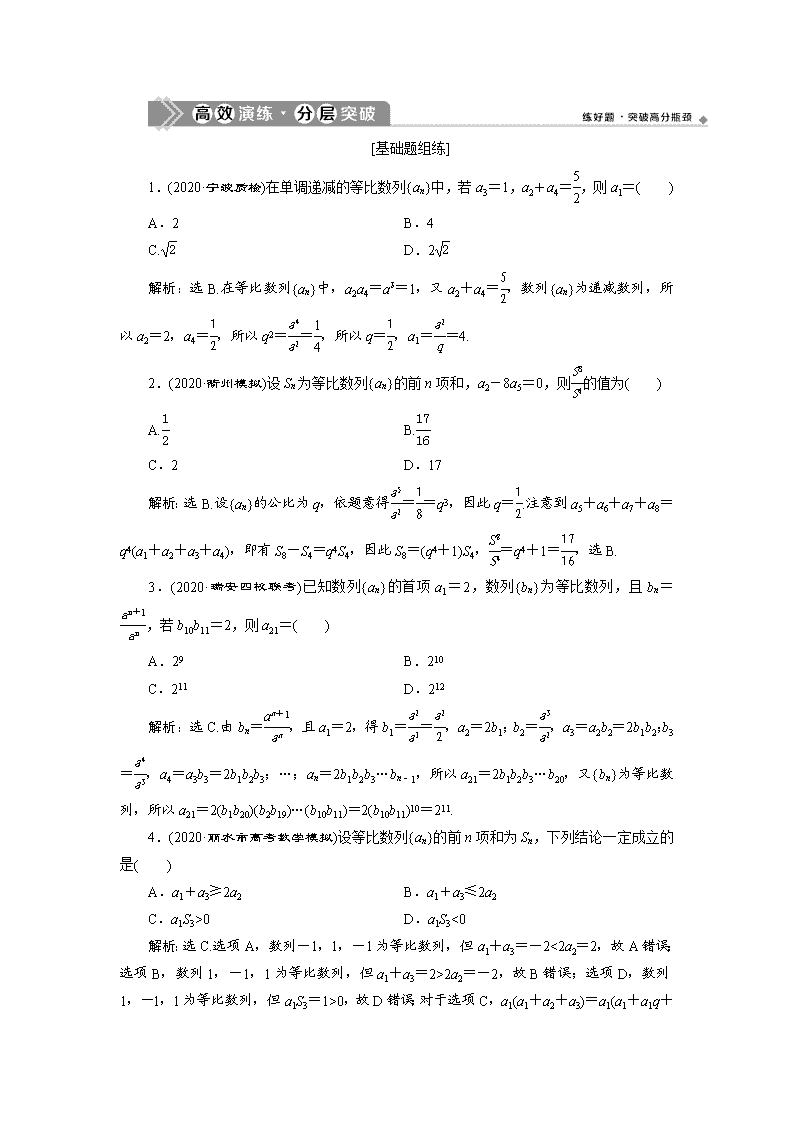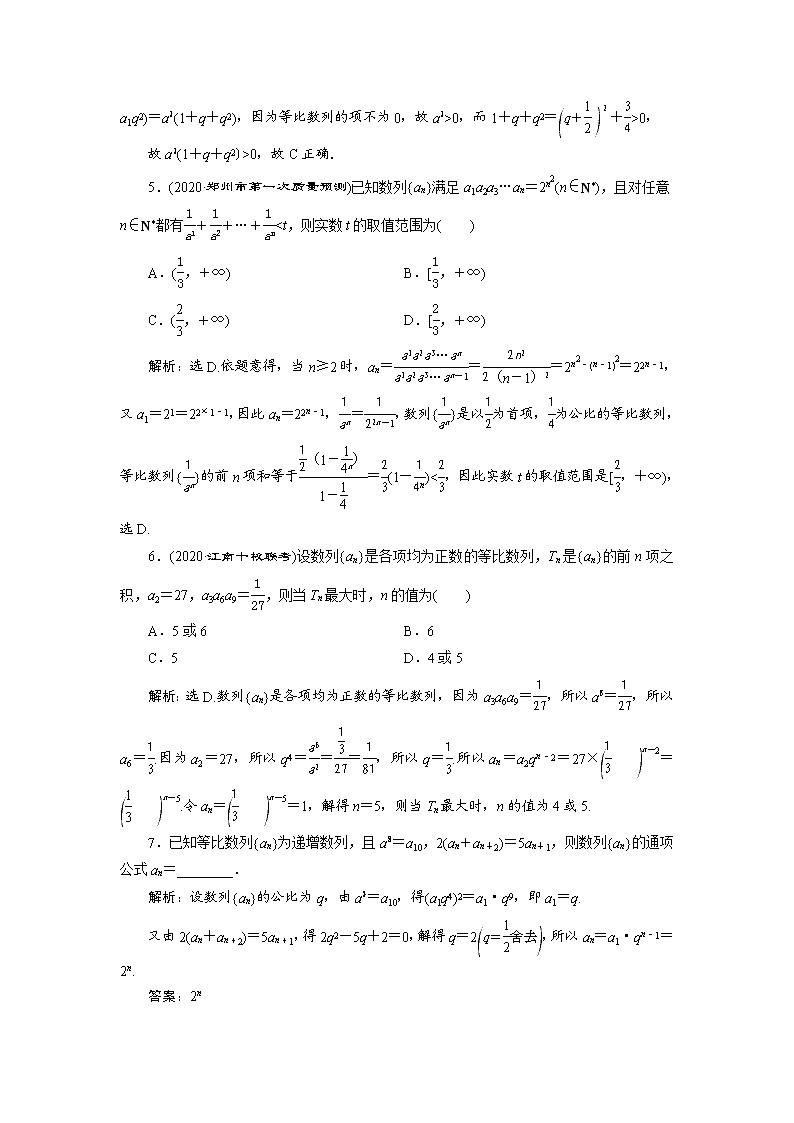2021届浙江新高考数学一轮复习高效演练分层突破：第六章　3 第3讲　等比数列及其前n项和 8页

‎[基础题组练]‎ ‎1．(2020·宁波质检)在单调递减的等比数列{an}中，若a3＝1，a2＋a4＝，则a1＝(　　)‎ A．2　　　　　　　　　　　　 B．4‎ C. D．2 解析：选B.在等比数列{an}中，a2a4＝a＝1，又a2＋a4＝，数列{an}为递减数列，所以a2＝2，a4＝，所以q2＝＝，所以q＝，a1＝＝4.‎ ‎2．(2020·衢州模拟)设Sn为等比数列{an}的前n项和，a2－8a5＝0，则的值为(　　)‎ A. B. C．2 D．17‎ 解析：选B.设{an}的公比为q，依题意得＝＝q3，因此q＝.注意到a5＋a6＋a7＋a8＝q4(a1＋a2＋a3＋a4)，即有S8－S4＝q4S4，因此S8＝(q4＋1)S4，＝q4＋1＝，选B.‎ ‎3．(2020·瑞安四校联考)已知数列{an}的首项a1＝2，数列{bn}为等比数列，且bn＝，若b10b11＝2，则a21＝(　　)‎ A．29 B．210‎ C．211 D．212‎ 解析：选C.由bn＝，且a1＝2，得b1＝＝，a2＝2b1；b2＝，a3＝a2b2＝2b1b2；b3＝，a4＝a3b3＝2b1b2b3；…；an＝2b1b2b3…bn－1，所以a21＝2b1b2b3…b20，又{bn}为等比数列，所以a21＝2(b1b20)(b2b19)…(b10b11)＝2(b10b11)10＝211.‎ ‎4．(2020·丽水市高考数学模拟)设等比数列{an}的前n项和为Sn，下列结论一定成立的是(　　)‎ A．a1＋a3≥2a2　　　　　 B．a1＋a3≤2a2‎ C．a1S3>0 D．a1S3<0‎ 解析：选C.选项A，数列－1，1，－1为等比数列，但a1＋a3＝－2<2a2＝2，故A错误；选项B，数列1，－1，1为等比数列，但a1＋a3＝2>2a2＝－2，故B错误；选项D，数列1，－1，1为等比数列，但a1S3＝1>0，故D错误；对于选项C，a1(a1＋a2＋a3)＝a1(a1＋a1q＋a1q2)＝a(1＋q＋q2)，因为等比数列的项不为0，故a>0，而1＋q＋q2＝＋>0，‎ 故a(1＋q＋q2)>0，故C正确．‎ ‎5．(2020·郑州市第一次质量预测)已知数列{an}满足a1a2a3…an＝2n2(n∈N*)，且对任意n∈N*都有＋＋…＋0)．(　　)‎ A．若b7≤a6，则b4＋b10≥a3＋a9‎ B．若b7≤a6，则b4＋b10≤a3＋a9‎ C．若b6≥a7，则b3＋b9≥a4＋a10‎ D．若b6≤a7，则b3＋b9≤a4＋a10‎ 解析：选C.因为数列{an}是等差数列，数列{bn}是等比数列(bn>0)，‎ 在A中，因为b7≤a6，b4＋b10≥2＝2b7，‎ a3＋a9＝2a6，所以b4＋b10≥a3＋a9不一定成立，故A错误；‎ 在B中，因为b7≤a6，b4＋b10≥2＝2b7，‎ a3＋a9＝2a6，所以b4＋b10≤a3＋a9不一定成立，故B错误；‎ 在C中，因为b6≥a7，所以b3＋b9≥2＝2b6，a4＋a10＝2a7，所以b3＋b9≥a4＋a10，故C正确；‎ 在D中，因为b6≤a7，所以b3＋b9≥2＝2b6，a4＋a10＝2a7，所以b3＋b9≤a4＋a10不一定成立，故D错误．‎ ‎3．已知直线ln：y＝x－与圆Cn：x2＋y2＝2an＋n交于不同的两点An，Bn，n∈N*，数列{an}满足：a1＝1，an＋1＝|AnBn|2，则数列{an}的通项公式为________．‎ 解析：圆Cn的圆心到直线ln的距离dn＝＝，半径rn＝，故an＋1＝|AnBn|2＝r－d＝2an，故数列{an}是以1为首项，2为公比的等比数列，故an＝2n－1(n∈N*)．‎ 答案：an＝2n－1(n∈N*)‎ ‎4．设数列{an}的前n项和为Sn，已知a1＝，且对任意正整数m，n都有am＋n＝am·an，若Sn0知，A(n)，B(n)，C(n)均大于0，于是＝＝＝q，‎ ＝＝＝q，‎ 即＝＝q，‎ 所以三个数A(n)，B(n)，C(n)组成公比为q的等比数列；‎ ‎(充分性)：若对任意n∈N*，三个数A(n)，B(n)，C(n)组成公比为q的等比数列，则 B(n)＝qA(n)，C(n)＝qB(n)，‎ 于是C(n)－B(n)＝q[B(n)－A(n)]，即an＋2－a2＝‎ q(an＋1－a1)，亦即an＋2－qan＋1＝a2－qa1.‎ 由n＝1时，B(1)＝qA(1)，‎ 即a2＝qa1，从而an＋2－qan＋1＝0.‎ 因为an>0，‎ 所以＝＝q.故数列{an}是首项为a1，公比为q的等比数列．‎ 综上所述，数列{an}是公比为q的等比数列的充分必要条件是：对任意n∈N*，三个数A(n)，B(n)，C(n)组成公比为q的等比数列．‎ ‎6．(2020·杭州市七校高三联考)已知等比数列{an}的公比为q(0a5，‎ 解得a2＝1，a5＝，‎ 由等比数列的性质可知a5＝a2·q3，解得q＝，‎ an＝a2·＝，‎ 所以数列{an}的通项公式为an＝.‎ ‎(2)由(1)可知bn＝an·(log2an)＝，‎ ‎{bn}的前n项和Tn＝b1＋b2＋b3＋…＋bn ‎＝2＋0＋＋＋＋…＋，‎ Tn＝1＋0＋＋＋＋…＋，‎ 两式相减可得 Tn＝1－－ ‎＝1－－ ‎＝1－－ ‎＝－ ‎＝，‎ 所以Tn＝.‎ ‎(3)因为Sn＝4，‎ 由<⇒2<2n(4－m)<6，‎ ‎2n(4－m)为偶数，因此只能取2n(4－m)＝4，‎ 所以有或⇒或.‎