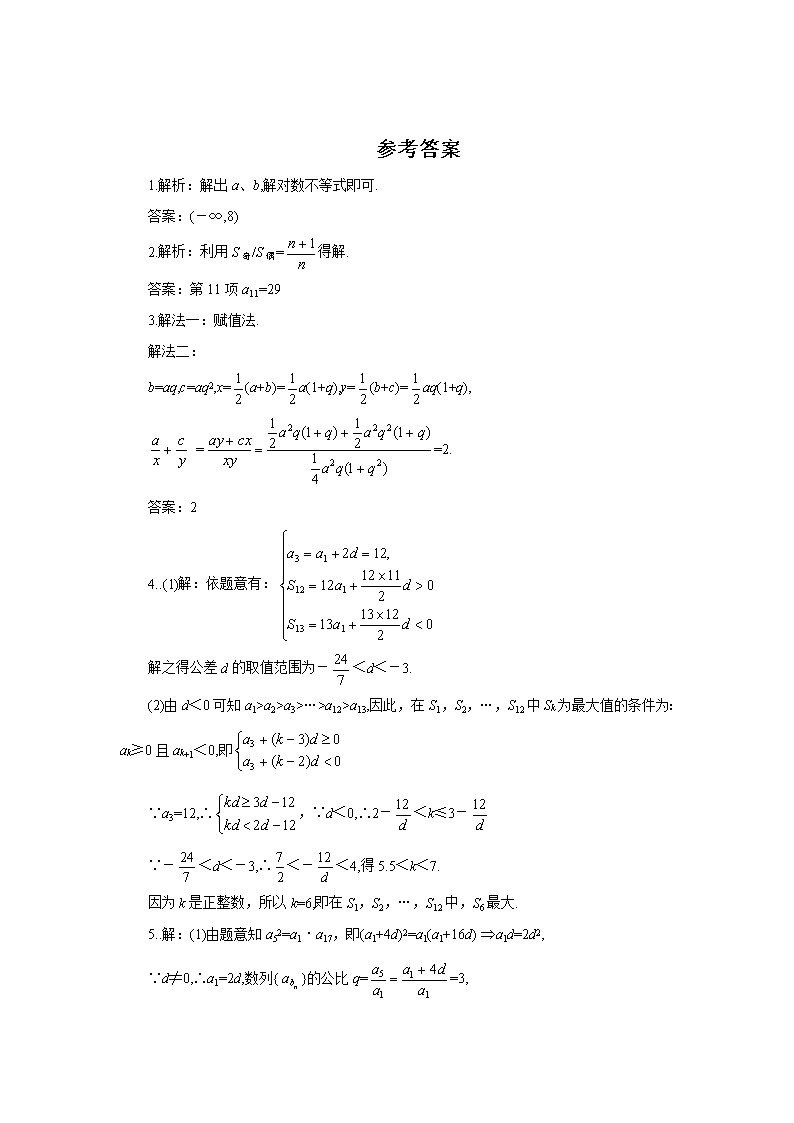- 97.00 KB
- 2021-06-23 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
高三数学复习之30分钟小练习(42)
1.已知a,b,a+b成等差数列,a,b,ab成等比数列,且00,S13<0.
(1)求公差d的取值范围;
(2)指出S1、S2、…、S12中哪一个值最大,并说明理由.
5.已知数列{an}为等差数列,公差d≠0,由{an}中的部分项组成的数列
a,a,…,a,…为等比数列,其中b1=1,b2=5,b3=17. 求数列{bn}的通项公式;
6.设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2·b4=a3,分别求出{an}及{bn}的前10项和S10及T10.
7.{an}为等差数列,公差d≠0,an≠0,(n∈N*),且akx2+2ak+1x+ak+2=0(k∈N*)
(1)求证:当k取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为x1,x2,…,xn,…,求证:数列为等差数列.
参考答案
1.解析:解出a、b,解对数不等式即可.
答案:(-∞,8)
2.解析:利用S奇/S偶=得解.
答案:第11项a11=29
3.解法一:赋值法.
解法二:
b=aq,c=aq2,x=(a+b)=a(1+q),y=(b+c)=aq(1+q),
==2.
答案:2
4..(1)解:依题意有:
解之得公差d的取值范围为-<d<-3.
(2)由d<0可知a1>a2>a3>…>a12>a13,因此,在S1,S2,…,S12中Sk为最大值的条件为:ak≥0且ak+1<0,即
∵a3=12,∴,∵d<0,∴2-<k≤3-
∵-<d<-3,∴<-<4,得5.5<k<7.
因为k是正整数,所以k=6,即在S1,S2,…,S12中,S6最大.
5..解:(1)由题意知a52=a1·a17,即(a1+4d)2=a1(a1+16d)a1d=2d2,
∵d≠0,∴a1=2d,数列{}的公比q==3,
∴=a1·3n-1 ①
又=a1+(bn-1)d= ②
由①②得a1·3n-1=·a1.∵a1=2d≠0,∴bn=2·3n-1-1.
6.解:∵{an}为等差数列,{bn}为等比数列,∴a2+a4=2a3,b2·b4=b32,
已知a2+a4=b3,b2·b4=a3,∴b3=2a3,a3=b32,
得b3=2b32,∵b3≠0,∴b3=,a3=.
由a1=1,a3=,知{an}的公差d=-,
∴S10=10a1+d=-.
由b1=1,b3=,知{bn}的公比q=或q=-,
7.证明:(1)∵{an}是等差数列,∴2ak+1=ak+ak+2,故方程akx2+2ak+1x+ak+2=0可变为(akx+ak+2)(x+1)=0,
∴当k取不同自然数时,原方程有一个公共根-1.
(2)原方程不同的根为xk=
天 星 教育网(www.tesoon.com) 版权所有
天 星 教育网(www.tesoon.com) 版权所有
天 星 教育网(www.tesoon.com) 版权所有
Tesoon.com
天 星版权
天·星om
权
天 星 教育网(www.tesoon.com) 版权所有
tesoon
天·星om
权
天·星om
权
Tesoon.com
天 星版权
tesoon
tesoon
tesoon
天 星