广东省2019年广州市普通高中毕业班综合测试（二）理科数学(解析版) 26页

‎2019年广州市普通高中毕业班综合测试（二）‎ 理科数学 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知复数在复平面内对应的点在第三象限，则实数的取值范围是（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎1．答案：B 解析：对应的点位于第三象限，所以．‎ ‎2．己知集合，则（ ）‎ A．或 B．或 C．或 D．或 ‎2．答案：D 解析：，，解得，所以，‎ 或．‎ ‎3．某公司生产三种不同型号的轿车，产量之比依次为，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为的样本，若样本中种型号的轿车比种型号的轿车少8辆，则（ ）‎ A．96‎ B．72‎ C．48‎ D．36‎ ‎3．答案：B 解析：设抽取三种型号的车的数量分别为，则根据题意可得，‎ 所以．‎ ‎4．执行如图所示的程序框图，则输出的值是（ ）‎ A．21‎ B．22‎ C．23‎ D．24‎ ‎4．答案：A 解析：‎ 输出．‎ ‎5．己知点与点关于直线对称，则点的坐标为（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎5．答案：D 解析：设，则中点在直线上，‎ 所以．‎ ‎6．从某班6名学生（其中男生4人，女生2人）中任选3人参加学校组织的社会实践活动．设所选3人中女生人数为，则数学期望（ ）‎ A．‎ B．1‎ C．‎ D．2‎ ‎6．答案：B 解析：‎ ‎7．已知：，其中，则（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎7．答案：D 解析：由，其中，可得，‎ ‎．‎ ‎8．过双曲线的左焦点作圆的切线，切点为，延长交双曲线右支交于点，若，则双曲线的离心率为（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎8．答案：A 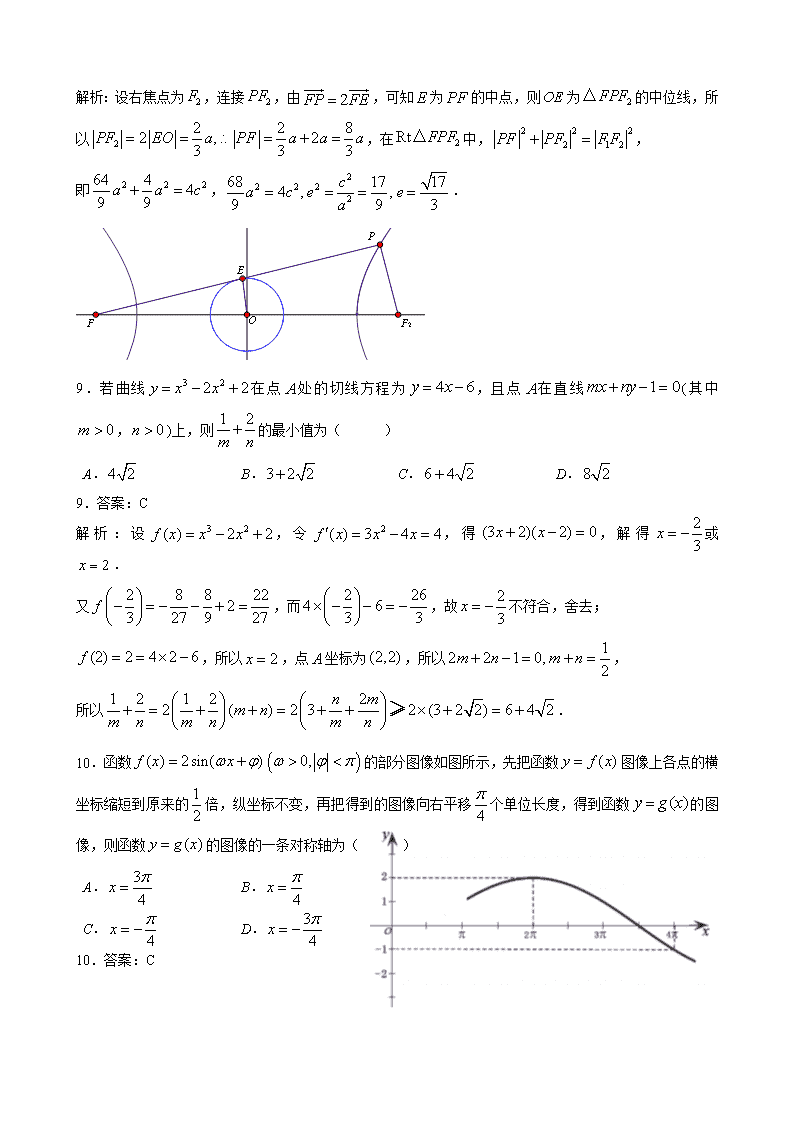解析：设右焦点为，连接，由，可知为的中点，则为的中位线，所以，在中，，‎ 即，．‎ ‎9．若曲线在点处的切线方程为，且点在直线(其中，)上，则的最小值为（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎9．答案：C 解析：设，令，得，解得或．‎ 又，而，故不符合，舍去；‎ ‎，所以，点坐标为，所以，‎ 所以．‎ ‎10．函数的部分图像如图所示，先把函数图像上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的图像向右平移个单位长度，得到函数的图像，则函数的图像的一条对称轴为（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎10．答案：C 解析：由图象可知，所以．各点的横坐标缩短到原来的倍，得，再把得到的图像向右平移个单位长度，得 ‎，由，‎ 所以，当时，得．‎ ‎11．已知点在直线上，点在直线上，的中点为，且 ‎，则的取值范围为（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎11．答案：B 解析：在直线上，所以，，由，‎ 得，解得，所以．‎ ‎12．若点与曲线上点的距离的最小值为，则实数的值为（ ）‎ A．‎ B．‎ C．‎ D．‎ ‎12．答案：D 解析：设，则，设，‎ 则，令，得，此时取得最小值，所以 ‎，显然，所以，‎ 又因为，所以，所以，此时．‎ 二、填空题：本题共4小题，每小题5分，共20分．‎ ‎13．若是夹角为的两个单位向量，向量，则 ．‎ ‎13．答案： ‎ 解析：，‎ 所以．‎ ‎14．若的展开式中的系数是80，则实数的值是 ．‎ ‎14．答案：2‎ 解析：的展开式中含的项为，所以．‎ ‎15．秦九韶是我国南宋著名数学家，在他的著作《数书九章》中有己知三边求三角形面积的方法：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减上，余四约之，为实，一为从隅，开平方得积．”如果把以上这段文字写成公式就是其中是的内角的对边．若，且成等差数列，则面积的最大值为 ．‎ ‎15．答案：‎ 解析： 因为，‎ 又因为，所以，即，‎ 因为成等差数列，所以，‎ 所以 ‎，当且仅当时等号成立．故面积的最大值为．‎ ‎16．有一个底面半径为，轴截面为正三角形的圆锥纸盒，在该纸盒内放一个棱长均为的四面体，并且四面体在纸盒内可以任意转动，则的最大值为 ．‎ ‎16．答案：‎ 解析：要使得四面体在纸盒内可以任意转动，且最大，则四面体的外接球就是圆锥的内切球，设该球的半径为，则，且，所以，解得．‎ 三、解答题：共70分，解答应写出文字说明、证明过程和演算步骤，第17～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答．‎ ‎（一）必考题：共60分．‎ ‎17．（本小题满分12分）‎ 己知是递增的等比数列，．‎ ‎（1）求数列的通项公式；‎ ‎（2）令，求数列的前项和．‎ ‎17．解法1：（1）设等比数列的公比为，因为，，‎ 所以 ……………………………………………………………………………………2分 解得 或 ………………………………………………………………………………4分 因为是递增的等比数列，所以，．………………………………………………5分 所以数列的通项公式为．………………………………………………………………6分 解法2：（1）设等比数列的公比为，因为，，‎ 所以，是方程的两个根．…………………………………………………………2分 解得或…………………………………………………………………………………4分 因为是递增的等比数列，‎ 所以，，则．…………………………………………………………………………5分 所以数列的通项公式为．………………………………………………………………6分 ‎（2）由（1）知．………………………………………………………………………………7分 则， ①…………………………8分 在①式两边同时乘以得，‎ ‎， ②…………………………9分 ‎①-②得，…………………………………………………10分 即，…………………………………………………………………………11分 所以．………………………………………………………………………12分 ‎18．（本小题满分12分）‎ 科研人员在对人体脂肪含量和年龄之间关系的研究中，获得了一些年龄和脂肪含量的简单随机样本数据，如下表：‎ x （年龄/岁）‎ ‎26‎ ‎27‎ ‎39‎ ‎41‎ ‎49‎ ‎53‎ ‎56‎ ‎58‎ ‎60‎ ‎61‎ y（脂肪量/%）‎ ‎14.5‎ ‎17.8‎ ‎21.2‎ ‎25.9‎ ‎26.3‎ ‎29.6‎ ‎31.4‎ ‎33.5‎ ‎35.2‎ ‎34.6‎ 根据上表的数据得到如下的散点图．‎ ‎（1）根据上表中的样本数据及其散点图：‎ ‎（i）求；‎ ‎（ii）计算样本相关系数（精确到0. 01），并刻画它们的相关程度．‎ ‎（2）若关于的线性回归方程为，求的值（精确到0.01），并根据回归方程估计年龄为50岁时人体的脂肪含量。‎ 附：‎ 参考数据：‎ 参考公式：相关系数 回归方程中斜率和截距的最小二乘估计公式分别为 ‎18．解：（1）根据上表中的样本数据及其散点图：‎ ‎（ⅰ）．…………………………………2分 ‎（ⅱ）…………3分 ‎ ………………………………4分 ‎ ．…………………………………………………………………………5分 因为，，‎ 所以．……………………………………………………………………………………………6分 由样本相关系数，可以推断人体脂肪含量和年龄的相关程度很强．………………………7分 ‎（2）因为回归方程为，即．‎ 所以．‎ ‎【或利用】……………………………10分 所以关于的线性回归方程为．‎ 将代入线性回归方程得．………………………………………11分 所以根据回归方程预测年龄为岁时人的脂肪含量为%．…………………………………12分 ‎19．（本小题满分12分）‎ 如图，在四棱锥中，底面为菱形，，且．‎ ‎（1）求证：平面平面；‎ ‎（2）若，求二面角的余弦值．‎ ‎19．（1）证明：取中点，连结，，，‎ 因为底面为菱形，，‎ 所以．‎ 因为为的中点，‎ 所以．………………………………………1分 在△中，， 为的中点，‎ 所以．‎ 设,则，，‎ 因为，所以．………………………………………2分 ‎【2分段另证：在△中，，为的中点，所以．‎ 在△ 和△ 中，因为，，，所以△ △ ．‎ 所以．所以．】‎ 因为，平面，平面，‎ 所以平面．……………………………………………………………………………………3分 因为平面，‎ 所以平面平面．…………………………………………………………………………4分 ‎（2）解法1：因为，，，‎ 平面，平面，‎ 所以平面．‎ 所以． ‎ 由（1）得，，‎ 所以，，所在的直线两两互相垂直．‎ ‎………………………5分 以为坐标原点，分别以，，所在直线为轴，轴，轴建立如图所示的空间直角坐标系．……………………………………………………………6分 设，则，，，，………………………………7分 所以，，，………………………………8分 设平面的法向量为，‎ 则 令，则，，‎ 所以．…………………………………………………………………………………9分 设平面的法向量为，‎ 则 令，则，，‎ 所以．……………………………………………………………………………………10分 设二面角为，由于为锐角，‎ 所以………………………………………………………………………………11分 ‎．‎ 所以二面角的余弦值为．…………………………………………………………12分 解法2：因为，，，平面，平面，‎ 所以平面．‎ 所以．…………………………………………………………………………………………5分 所以，．‎ 过点作，为垂足，‎ 过点作交于点，连接，……6分 因为，，‎ 所以，即．‎ 所以为二面角的平面角．………7分 在等腰△中，，，‎ 根据等面积法可以求得．…………………………………………………………………8分 进而可以求得，‎ 所以，．…………………………………………………………………………9分 在△中，，，，‎ 所以．‎ 在△中，，，，‎ 所以，即．…………………………10分 在△中，，，，‎ 所以………………………………………………………………11分 ‎．‎ 所以二面角的余弦值为．…………………………………………………………12分 ‎20．（本小题满分12分）‎ 在平面直角坐标系中，动点分别与两个定点的连线的斜率之积为 ‎(1)求动点的轨迹的方程；‎ ‎(2)设过点的直线与轨迹交于两点，判断直线与以线段为直径的圆的位置关系，并说明理由．‎ ‎20．解：（1）设动点的坐标为，‎ 因为，，…………………………………………………1分 所以．……………………………………………………………………2分 整理得．………………………………………………………………………………………3分 所以动点的轨迹的方程．………………………………………4分 ‎（2）解法1：过点的直线为轴时，显然不合题意．……………………………………………5分 所以可设过点的直线方程为， ‎ 设直线与轨迹的交点坐标为，‎ 由得．………………………………………………………6分 因为，‎ 由韦达定理得=，=．…………………………………………………7分 注意到=．‎ 所以的中点坐标为．…………………………………………………………8分 因为 ‎．………………………………………………9分 点到直线的距离为．………………………………………10分 因为，……………………………………………………………11分 即，‎ 所以直线与以线段为直径的圆相离．……………………………………………………12分 解法2：①当过点的直线斜率不存在时，直线方程为，与交于和两点，此时直线与以线段为直径的圆相离．…………………………………5分 ‎②当过点的直线斜率存在时，设其方程为，‎ 设直线与轨迹的交点坐标为，，‎ 由得．……………………………………………6分 因为，‎ 由韦达定理得，．…………………………………………………7分 注意到．‎ 所以的中点坐标为．…………………………………………………………8分 因为 ‎．………………………………………………9分 点到直线的距离为．……………………………………10分 因为，……………………………………………………………11分 即， ‎ 所以直线与以线段为直径的圆相离．……………………………………………………12分 ‎21．（本小题满分12分）‎ 已知函数．‎ ‎（1）讨论函数的单调性；‎ ‎（2）若函数有两个零点，求的取值范围，并证明．‎ ‎21．（1）解：因为，函数的定义域为，‎ 所以．………………………………………………………………1分 当时，，‎ 所以函数在上单调递增．…………………………………………………………………2分 当时，由，得（负根舍去），‎ 当时，，当时，，‎ 所以函数在上单调递减；在上单调递增．……………………………3分 综上所述，当时，函数在上单调递增；当时，函数在上单调递减，在上单调递增．………………………………………………………………………4分 ‎（2）先求的取值范围：‎ ‎【方法1】由（1）知，当时，在上单调递增，不可能有两个零点，不满足条件．‎ ‎………………………………………………………………………5分 当时，函数在上单调递减，在上单调递增，‎ 所以，‎ 要使函数有两个零点，首先，解得．………………6分 因为，且，‎ 下面证明．‎ 设，则．‎ 因为，所以．‎ 所以在上单调递增，‎ 所以．‎ ‎【若考生书写为：因为当时，，且．此处不扣分】‎ 所以的取值范围是．…………………………………………………………………………7分 ‎【方法2】由，得到．………………………………………………5分 设，则．‎ 当时，，当时，，‎ 所以函数在上单调递减，在上单调递增． ‎ 所以由．…………………………………………………………………6分 因为时，，且，‎ 要使函数有两个零点，必有． ‎ 所以的取值范围是．…………………………………………………………………………7分 再证明：‎ ‎【方法1】因为，是函数的两个零点，不妨设，令，则．‎ 所以即．……………………………………………………8分 所以，即，，．‎ 要证，即证．………………………………………………………9分 即证，即证．‎ 因为，所以即证，‎ 或证．………………………………………………………………10分 设，．‎ 即，．‎ 所以．‎ ‎【用其他方法判断均可，如令分子为，通过多次求导判断】‎ 所以在上单调递减，………………………………………………………………………11分 所以． ‎ 所以．…………………………………………………………………………………12分 ‎【方法2】因为，是函数有两个零点，不妨设，令，则．‎ 所以即．……………………………………………………8分 所以，即，，． ‎ 要证，需证．………………………………………………………9分 即证，即证．‎ 因为，所以即证．…………………………………………………10分 设，‎ 则，． ‎ 所以在上单调递减，………………………………………………………………………11分 所以．‎ 所以．…………………………………………………………………………………12分 ‎【方法3】因为，是函数有两个零点，不妨设，令，则．‎ 所以即．………………………………………………………8分 要证，需证．………………………………………………………9分 只需证．‎ 即证，即证．‎ 即证．…………………………………………………………………………10分 因为，所以，即．………………………………………………11分 所以．‎ 而， ‎ 所以成立．‎ 所以．…………………………………………………………………………………12分 ‎【方法4】因为，是函数有两个零点，不妨设，令，则．‎ 由已知得即．…………………………………………………8分 先证明，即证明． ‎ 设，则．‎ 所以在上单调递增，所以，所证不等式成立．………………………9分 所以有．………………………………………………………10分 即．‎ 因为（），……………………………………………………………………11分 所以，即．‎ 所以．…………………………………………………………………………………12分 ‎【方法5】要证，其中，，‎ 即证．…………………………………………………………………………………8分 利用函数的单调性，只需证明． ‎ 因为，所以只要证明，其中．………9分 构造函数，，‎ 则．…………………………………………10分 因为 ‎（利用均值不等式）‎ ‎，‎ 所以在上单调递减．…………………………………………………………………11分 所以．‎ 所以在上恒成立．‎ 所以要证的不等式成立．……………………………………………………………12分 ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．‎ ‎22．[选修4 —4：坐标系与参数方程]（本小题满分10分）‎ 在直角坐标系中，倾斜角为的直线的参数方程为（为参数）．在以坐标原点为极点，轴正半轴为极轴的极坐标系中，曲线的极坐标方程为．‎ ‎（1）求直线的普通方程与曲线的直角坐标方程；‎ ‎（2）若直线与曲线交于两点，且，求直线的倾斜角．‎ ‎22．（1）解法1：因为直线的参数方程为（为参数），‎ 当时，直线的直角坐标方程为．…………………………………………………………1分 当时，直线的直角坐标方程为．……………………………………3分 因为，…………………………………………………………………………4分 因为，所以．‎ 所以的直角坐标方程为．………………………………………………………5分 解法2：因为直线的参数方程为（为参数），‎ 则有 ……………………………………………………………2分 所以直线的直角坐标方程为 ．………………………3分 因为，…………………………………………………………………………4分 因为，所以．‎ 所以的直角坐标方程为．………………………………………………………5分 ‎（2）解法1：曲线的直角坐标方程为，‎ 将直线的参数方程代入曲线的方程整理，得．……………6分 因为，可设该方程的两个根为，，‎ 则 ，．……………………………………………………7分 所以 ‎ ‎．…………………………………………………………8分 整理得，‎ 故．…………………………………………………………………………………9分 因为，所以或，‎ 解得或 综上所述，直线的倾斜角为或．…………………………………………………………………10分 解法2：直线与圆交于，两点，且，‎ 故圆心到直线的距离．…………………………………………………6分 ‎①当时，直线的直角坐标方程为，符合题意．…………………………………………7分 ‎②当时，直线的方程为．‎ 所以，………………………………………………………………8分 整理得．‎ 解得．………………………………………………………………………………………………9分 综上所述，直线的倾斜角为或．…………………………………………………………………10分 ‎23．[选修4—5：不等式选讲]（本小题满分10分）‎ 己知函数．‎ ‎（1）当时，解不等式；‎ ‎（2）若存在实数，使得成立，求实数的取值范围．‎ ‎23．（1）解：当时，由，得．…………………………………………1分 当时，， 解得．‎ 当时，，解得．…………………………………………………………4分 综上可知，不等式的解集为 ．……………………………………5分 ‎（2）解法1：由，得．‎ 则．…………………………………………………………………………………6分 令，‎ 则问题等价于 因为……………………………………………………………………9分 ‎．‎ 所以实数的取值范围为．…………………………………………………………………10分 解法2：因为，………………………………………………6分 即，则．……………………………………………7分 所以，…………………………………………8分 当且仅当时等号成立．……………………………………………………………………………9分 所以．‎ 所以实数的取值范围为．…………………………………………………………………10分