数学理卷·2017届北京市平谷区高三下学期质量监控（2017 9页

平谷区２０１６－２０１７学年度第二学期质量监控试卷 高三数学(理)‎ 考 生 须知 1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分,考试时间为120分钟 .‎ 2. 试题所有答案必须书写在答题卡上，在试卷上作答无效.‎ 3. 考试结束后，将答题卡交回，试卷按学校要求保存好.‎ 第Ⅰ卷（选择题 共40分）‎ 一、选择题：（本大题共8小题，每小题5分，共40分；在每个小题列出的四个选项中，只有一项是符合要求的.）‎ ‎1.已知集合，则为 ‎ A． B． C． D． ‎ ‎2.下列函数中，既是偶函数又存在零点的是 ‎ A． B． C． D． ‎ ‎3.已知实数、满足：，则的最大值为 A．2 B．0 C．-1 D．-3 ‎ ‎4.已知是两条不同的直线，是平面，且，那么“”是“”的 A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎ 开始 S=0，i=1‎ 结束 i=i+2‎ i >7?‎ 输出S 是 否 S=S+i ‎5. 执行如右图所示的程序框图，则输出的值是 ‎ A． 9 B. 16 C. 25 D. 27‎ ‎6．若将函数的图像向右平移个单位，‎ 所得图像关于轴对称，则的最小正值是 A． B． C． D． ‎ ‎7.已知点及抛物线上一动点，‎ 则的最小值为 A． B． C． 3 D． 4 ‎ ‎8、某位股民购进某只股票，在接下来的交易时间内，他的这只股票先经历了5次涨停(每次上涨10%)，又经历了5次跌停(每次下跌10%)，则该股民这只股票的盈亏情况(不考虑其他费用)为 A．略有盈利 B．略有亏损 C．没有盈利也没有亏损 D．无法判断盈亏情况 第Ⅱ卷（非选择题 共110分）‎ 二、填空题：（本大题共6小题，每小题5分，共30分.）‎ ‎9.设是虚数单位，则复数等于________________.‎ ‎10．在极坐标系中，设曲线和直线交于、两点，则_ .‎ ‎11.已知数列是递增的等比数列， ，，则数列的前6项和等于 . ‎ ‎12．在平面直角坐标系中，若方程表示双曲线，则实数的范围_____________；若此双曲线的离心率为，则双曲线的渐近线方程为________.‎ ‎13.如图，在矩形中，,点为的中点，如果，那么的值是 ． ‎ ‎14. 已知函数. ‎ ‎(i) 当时，满足不等式的的取值范围为_________；‎ ‎(ii) 若函数的图象与轴没有交点，则实数的取值范围为_____________.‎ 三、解答题：(本大题共6小题，共80分；解答应写出文字说明，证明过程或演算步骤.）‎ ‎15.(本小题满分13分)‎ 在中，角，，的对边分别是，,．‎ ‎（Ⅰ）求边的值； ‎ ‎（Ⅱ） 若，求的面积．‎ ‎16. 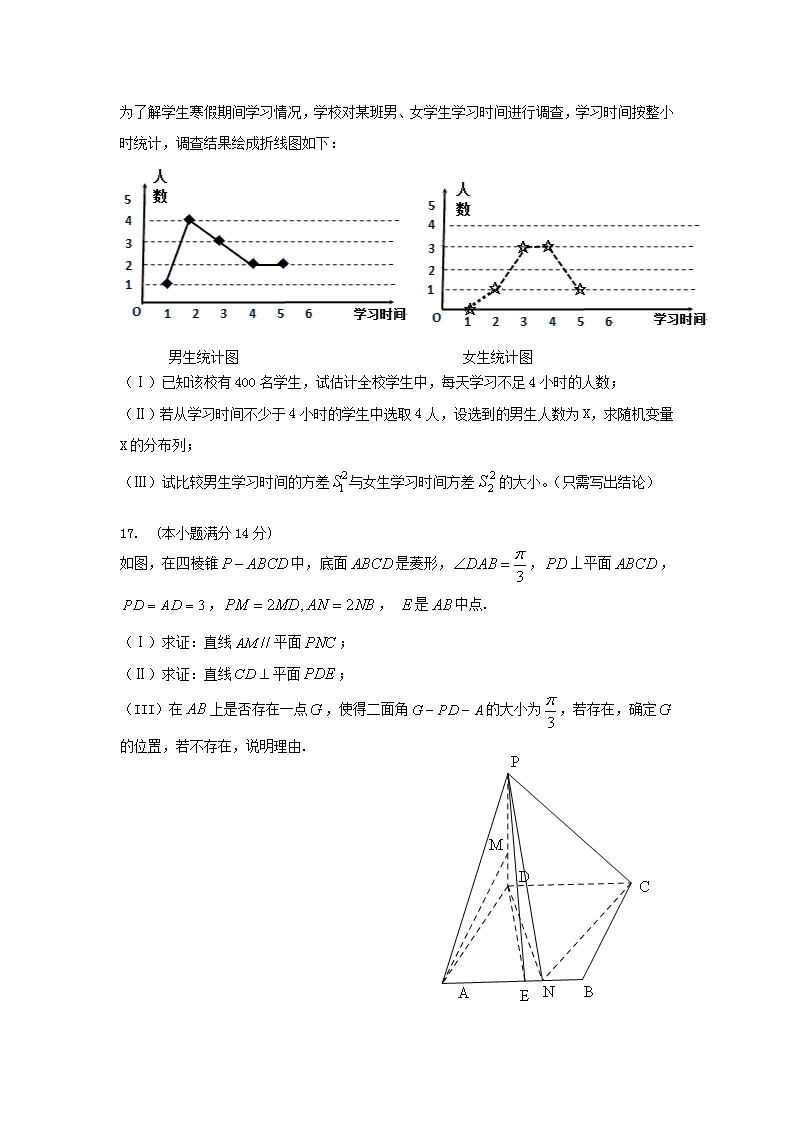(本小题满分13分)‎ 为了解学生寒假期间学习情况，学校对某班男、女学生学习时间进行调查，学习时间按整小时统计，调查结果绘成折线图如下：‎ ‎ 男生统计图 女生统计图 ‎（Ⅰ）已知该校有400名学生，试估计全校学生中，每天学习不足4小时的人数；‎ ‎（Ⅱ）若从学习时间不少于4小时的学生中选取4人，设选到的男生人数为X，求随机变量X的分布列；‎ ‎（Ⅲ）试比较男生学习时间的方差与女生学习时间方差的大小。（只需写出结论）‎ ‎17. (本小题满分14分)‎ 如图，在四棱锥中，底面是菱形，，⊥平面，，， 是中点.‎ ‎（Ⅰ）求证：直线平面；‎ ‎（Ⅱ）求证：直线平面； ‎ ‎（III）在上是否存在一点，使得二面角的大小为，若存在，确定的位置，若不存在，说明理由. ‎ ‎ ‎ ‎18．(本小题满分13分)‎ 已知函数．‎ ‎（Ⅰ）如果在处取得极值，求的值；‎ ‎（Ⅱ）求函数的单调区间；‎ ‎（III）当时，过点存在函数曲线的切线，求的取值范围.‎ ‎19.(本小题满分14分)‎ 已知椭圆C：经过点，离心率为， 为坐标原点.‎ ‎（Ⅰ）求椭圆C的方程； ‎ ‎（Ⅱ）若点为椭圆上一动点，点与点的垂直平分线交轴于点，求的最小值.‎ ‎20.(本小题满分13分)‎ 对于数列，若满足，则称数列为“0-1数列”.‎ 若存在一个正整数，若数列中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等，则称数列是“k阶可重复数列”，‎ 例如数列因为与按次序对应相等，所以数列是“4阶可重复数列”.‎ ‎（Ⅰ）分别判断下列数列 是否是“5阶可重复数列”？如果是，请写出重复的这5项；‎ ‎（Ⅱ）若项数为的数列一定是 “3阶可重复数列”，则的最小值是多少？说明理由；‎ ‎（III）假设数列不是“5阶可重复数列”，若在其最后一项后再添加一项0或1，均可使新数列是“5阶可重复数列”，且，求数列的最后一项的值.‎ 平谷区2016-2017学年度第二学期质量监控试题 高三数学（理）参考答案 一.选择题：本大题共8小题，每小题5分，共40分.‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A C A ‎ D B A C B 二.填空题：本大题共6小题，每小题5分，共30分.（两空题，第一空3分，第二空2分）‎ ‎9. ； 10. ； 11. 63 ； ‎ ‎12. m >0 ， ； 13. 9 ； 14. . ，‎ 三、解答题：(本大题共6小题，共80分；解答应写出文字说明，证明过程或演算步骤.）‎ ‎15.(本小题满分13分)‎ 解：因为 可得……………4分 因为 所以 即 所以 因为所以 所以面积……………13分 ‎16.(本小题满分13分)‎ 解：（Ⅰ）每天学习不足4小时的人数为：人．……………4分 ‎ （Ⅱ）学习时间不少于4本的学生共8人，其中男学生人数为4人，故的取值为 ‎．‎ 由题意可得； ；‎ ‎； ；‎ ‎．‎ 所以随机变量的分布列为 随机变量的均值．…………10分 ‎（Ⅲ）．…………………………………………………………………………13分 ‎17. (本小题满分14分)‎ 证明：（Ⅰ）在上去一点，使，连接，‎ 因为，‎ 所以，‎ 所以 所以为平行四边形 即 又平面 所以直线平面……………..5分 ‎（Ⅱ）因为是中点，底面是菱形，，所以 因为，所以，即.又⊥平面,所以 又所以直线平面……………..9分 ‎（III）由（Ⅱ）问 可知相互垂直，以为原点， 如图建立空间直角坐标系 则 设面的法向量 设面的法向量 解得 所以与重合.点的位置为所求………..14分 ‎18. (本小题满分13分)‎ 解：（Ⅰ）函数的定义域为R．所以 ‎ ‎∵函数在处取得极值 ‎∴，解得：k=0‎ 当k=0时，，‎ ‎∴函数在处取得极小值，符合题意。………..3分 ‎（Ⅱ）因为．‎ ①当时， 恒成立，所以在为减函数 ‎②当时，令 ， 则，‎ 当时，，在上单调递减；‎ 当时，，在上单调递增；‎ ‎…………………………………8分 ‎（III）设切点坐标为，‎ 则切线方程为 即 将代入得．‎ ‎ ‎ 令， 所以 ．‎ 当时，．‎ 所以 当时，，函数在上单调递增；‎ 当时，，在上单调递减． ‎ 所以 当时，，无最小值．‎ 当时，存在切线； ……………..13分 ‎19.(本小题满分14分)‎ ‎（Ⅰ）解：离心率为，所以，故，椭圆C为 把点带入得，所以椭圆的方程为. ……………5分 ‎（Ⅱ）解：由题意，直线的斜率存在，设点，‎ ‎ 则线段的中点的坐标为， 且直线的斜率，…7分 ‎ 由点关于直线的对称点为，得直线，‎ ‎ 故直线的斜率为，且过点， ‎ ‎ 所以直线的方程为：， ………9分 ‎ 令，得，则，‎ ‎ 由，得， 化简，得. …………11分 ‎ 所以 .…………13分 ‎ 当且仅当，即时等号成立.‎ ‎ 所以的最小值为. ………… 14分 ‎20.(本小题满分13分)‎ 解：（Ⅰ）10101 ….3分 ‎（Ⅱ）因为数列的每一项只可以是0或1，所以连续3项共有种不同的情形.‎ 若m＝11，则数列中有9组连续3项，则这其中至少有两组按次序对应相等，即项数为11的数列一定是“3阶可重复数列”；若m＝10，数列0,0,1,0,1,1,1,0,0,0不是“3阶可重复数列”；则时，均存在不是“3阶可重复数列”的数列.所以，要使数列一定是“3阶可重复数列”，则m的最小值是11. ……….8分 ‎（III）由于数列在其最后一项后再添加一项0或1，均可使新数列是“5阶可重复数列”，即在数列的末项后再添加一项，则存在，‎ 使得与按次序对应相等，或与按次序对应相等， ‎ 如果与不能按次序对应相等，那么必有，，使得、与按次序对应相等. ‎ 此时考虑和，其中必有两个相同，这就导致数列中有两个连续的五项恰按次序对应相等，从而数列是“5阶可重复数列”，这和题设中数列不是“5阶可重复数列”矛盾！所以与按次序对应相等，从而 ‎……….14分