数学卷·2018届江苏省苏州市高三上学期期末调研测试（2018 16页

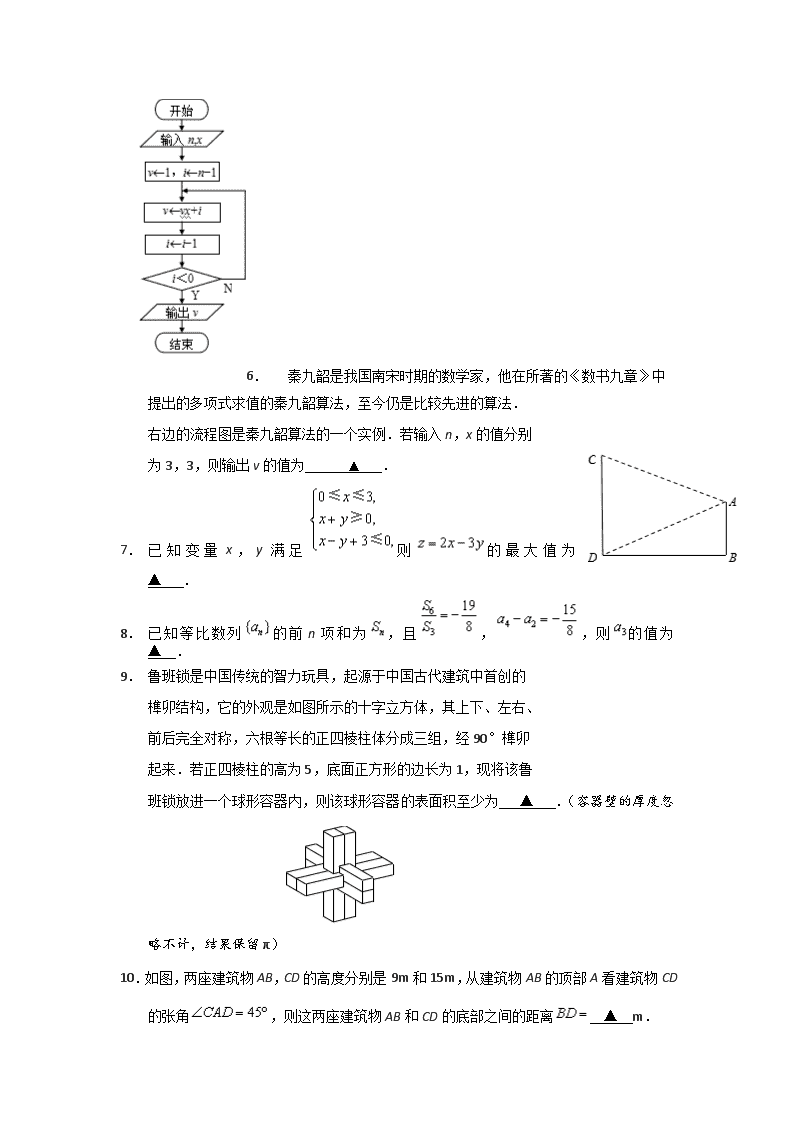
江苏省苏州市2018届高三上学期期末调研测试 ‎ 数学Ⅰ试题 2018．1‎ 参考公式：球的表面积公式S=4πr2，其中r为球的半径．‎ 一、填空题：本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请把答案直接填在答题卡相应位置上．‎ ‎1． 已知i为虚数单位，复数的模为 ▲ ．‎ ‎2． 已知集合，，且，则正整数 ▲ ．‎ ‎3． 在平面直角坐标系xOy中，抛物线的焦点坐标为 ▲ ．‎ ‎4． 苏州轨道交通1号线每5分钟一班，其中，列车在车站停留0.5 分钟，假设乘客到达站台的时刻是随机的，则该乘客到达站台 立即能乘上车的概率为 ▲ ． ‎ ‎5． 已知，，则正实数 ▲ ．‎ ‎6． 秦九韶是我国南宋时期的数学家，他在所著的《数书九章》中 提出的多项式求值的秦九韶算法，至今仍是比较先进的算法． 右边的流程图是秦九韶算法的一个实例．若输入n，x的值分别 为3，3，则输出v的值为 ▲ ．‎ ‎7． 已知变量x，y满足则的最大值为 ▲ ． ‎ ‎8． 已知等比数列的前n项和为，且，，则的值为 ▲ ．‎ ‎9． 鲁班锁是中国传统的智力玩具，起源于中国古代建筑中首创的 榫卯结构，它的外观是如图所示的十字立方体，其上下、左右、 前后完全对称，六根等长的正四棱柱体分成三组，经90°榫卯 起来．若正四棱柱的高为5，底面正方形的边长为1，现将该鲁 班锁放进一个球形容器内，则该球形容器的表面积至少为 ▲ ．（容器壁的厚度忽略不计，结果保留π）‎ ‎10．如图，两座建筑物AB，CD的高度分别是9m和15m，从建筑物AB的顶部A看建筑物CD的张角，则这两座建筑物AB和CD的底部之间的距离 ▲ m． ‎ ‎11．在平面直角坐标系xOy中，已知过点的圆和直线 x + y = 1相切，且圆心在直线 y = -2x 上，则圆C的标准方程为 ▲ ．‎ ‎12．已知正实数a，b，c满足，，则的取值范围是 ▲ ． ‎ ‎13．如图，△ABC为等腰三角形，，，以A为圆心，1为半径的圆分别交AB，AC与点E，F，点P是劣弧上的一点，则的取值范围是 ▲ ．‎ ‎14．已知直线y＝a分别与直线，曲线交于点A，B，则线段AB长度的最小值为 ▲ ．‎ ‎ ‎ ‎ ‎ ‎ ‎ 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15．（本小题满分14分）‎ 已知函数．‎ ‎（1）求函数的最小值，并写出取得最小值时自变量x的取值集合；‎ ‎（2）若，求函数的单调增区间．‎ ‎ ‎ ‎ ‎ ‎16．（本小题满分14分）‎ 如图，在正方体中，已知E，F，G，H分别是A1D1，B1C1，D1D，C1C的中点．‎ ‎（1）求证：EF∥平面ABHG；‎ ‎（2）求证：平面ABHG⊥平面CFED．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎17. （本小题满分14分）‎ 如图，B,C分别是海岸线上的两个城市，两城市间由笔直的海滨公路相连，B，C之间的距离为100km，海岛A在城市B的正东方50处．从海岛A到城市C，先乘船按北偏西θ角（，其中锐角的正切值为）航行到海岸公路P处登陆，再换乘汽车到城市C．已知船速为25km/h，车速为75km/h. ‎ ‎（1）试建立由A经P到C所用时间与的函数解析式；‎ ‎（2）试确定登陆点P的位置，使所用时间最少，并说明理由．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18．（本小题满分16分）‎ 在平面直角坐标系xOy中，椭圆的离心率为，椭圆上动点到一个焦点的距离的最小值为．‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）已知过点的动直线l与椭圆C交于 A，B 两点，试判断以AB为直径的圆是否恒过定点，并说明理由．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎19. （本小题满分16分）‎ 已知各项是正数的数列的前n项和为．‎ ‎（1）若（nÎN，n≥2），且．‎ ‎① 求数列的通项公式；‎ ‎② 若对任意恒成立，求实数的取值范围；‎ ‎（2）数列是公比为q（q＞0， q¹1）的等比数列，且{an}的前n项积为．若存在正整数k，对任意nÎN，使得为定值，求首项的值．‎ ‎ ‎ ‎ ‎ ‎20. （本小题满分16分）‎ 已知函数 ‎（1）当时，求函数的单调区间；‎ ‎（2）若方程在区间(0,+¥)上有实数解，求实数a的取值范围；‎ ‎（3）若存在实数，且，使得，求证：．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 数学Ⅱ（附加题） 2018．1‎ ‎ ‎ ‎21．【选做题】本题包括、、、四小题，请选定其中两题，并在相应的答题区域内作答，若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．‎ ‎．选修4 - 1：几何证明选讲（本小题满分10分）‎ 如图，，与圆O分别切于点B，C，点P为圆O上异于点B，C的任意一点，于点D，于点E，于点F. ‎ 求证：.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎．选修4 - 2：矩阵与变换（本小题满分10分）‎ 已知，，求．‎ ‎ ‎ ‎ ‎ ‎．选修4 - 4：坐标系与参数方程（本小题满分10分）‎ 在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为，若直线l与曲线C相交于A，B两点，求△AOB的面积．‎ ‎．选修4 - 5：不等式选讲（本小题满分10分）‎ 已知a，b，c∈R，，若对一切实数a，b，c恒成立，求实数x的取值范围．‎ ‎ ‎ ‎【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎22．（本小题满分10分）‎ 如图，已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB，且ABBP2，AD=AE=1，AE⊥AB，且AE∥BP．‎ ‎（1）求平面PCD与平面ABPE所成的二面角的余弦值；‎ ‎（2）线段PD上是否存在一点N，使得直线BN与 平面PCD所成角的正弦值等于？若存在，试确定 点N的位置；若不存在，请说明理由．‎ ‎ ‎ ‎23．（本小题满分10分）‎ 在正整数集上定义函数，满足，且．‎ ‎（1）求证：；‎ ‎（2）是否存在实数a，b，使，对任意正整数n恒成立，并证明你的结论．‎ ‎ ‎ 参考答案 一、填空题（共70分）‎ ‎1． 2．2 3． 4． 5． 6．48 7． 8． 9． ‎ ‎10．18 11． 12． 13． 14．‎ 二、解答题（共90分）‎ ‎15. 解（1）‎ ‎ 2分 ‎． 4分 当，即时，取得最小值0．‎ 此时，取得最小值时自变量x的取值集合为． 7分 ‎（注：结果不写集合形式扣1分）‎ ‎（2）因为，‎ 令， 8分 解得， 10分 又，令，，令，，‎ 所以函数在的单调增区间是和． 14分 ‎（注：如果写成两区间的并集，扣1分，其中写对一个区间给2分）‎ ‎16. 证明：（1）因为E，F是A1D1，B1C1的中点，所以，‎ 在正方体中，A1B1∥AB，‎ ‎（注：缺少A1B1∥AB扣1分）‎ 所以． 3分 又平面ABHG，AB平面ABHG，‎ ‎（注：缺少AB平面ABHG不扣分）‎ 所以EF∥平面ABHG． 6分 ‎（2）在正方体ABCD−A1B1C1D1中，CD ^平面BB1C1C，‎ 又平面，所以．① 8分 设，△BCH≌△，所以，‎ 因为∠HBC+∠PHC=90°，所以+∠PHC=90°．‎ 所以，即．② 11分 由①②，又，DC，CFÌ平面CFED，‎ 所以平面CFED．‎ 又平面ABHG，‎ 所以平面ABHG⊥平面CFED． 14分 ‎ （注：缺少平面ABHG，此三分段不给分）‎ ‎ ‎ ‎17. 解（1）由题意，轮船航行的方位角为θ，所以，，‎ 则，． ‎ ‎． 4分 ‎（注：AP，BP写对一个给2分）‎ 由A到P所用的时间为，‎ 由P到C所用的时间为， 6分 所以由A经P到C所用时间与θ的函数关系为 ． 8分 函数的定义域为，其中锐角的正切值为. ‎ ‎（2）由（1），，，‎ ‎，令，解得， 10分 设θ0Î，使 θ0‎ ‎0‎ 减函数 极小值 增函数 ‎ 12分 所以，当时函数f(θ)取得最小值，此时BP=≈17.68 ，‎ 答：在BC上选择距离B为17.68 处为登陆点，所用时间最少． 14分 ‎（注：结果保留根号，不扣分）‎ ‎ ‎ ‎18. 解（1）由题意，故， 1分 又椭圆上动点到一个焦点的距离的最小值为，所以，‎ ‎ 2分 解得，，所以， 4分 所以椭圆C的标准方程为. 6分 ‎（2）当直线l的斜率为0时，令，则，‎ 此时以AB为直径的圆的方程为． 7分 当直线l的斜率不存在时，以AB为直径的圆的方程为， 8分 联立解得，即两圆过点．‎ 猜想以AB为直径的圆恒过定点． 9分 对一般情况证明如下：‎ 设过点的直线l的方程为与椭圆C交于,‎ 则整理得，‎ 所以． 12分 ‎（注：如果不猜想，直接写出上面的联立方程、韦达定理，正确的给3分）‎ 因为 ‎，‎ 所以．‎ 所以存在以AB为直径的圆恒过定点T，且定点T的坐标为． 16分 ‎19. 解（1）①当时，由 ①‎ 则 ②‎ ‎②-①得，即， 2分 当时，由①知，即，‎ 解得或（舍），‎ 所以，即数列为等差数列，且首项，‎ 所以数列的通项公式为. 5分 ‎（注：不验证扣1分）‎ ‎②由①知，，所以，‎ 由题意可得对一切恒成立，‎ 记，则，，‎ 所以，， 8分 当时，，当时，，且，，，‎ 所以当时，取得最大值，‎ 所以实数的取值范围为. 11分 ‎（2）由题意，设（），，两边取常用对数，‎ ‎． ‎ 令，‎ 则数列是以为首项，为公差的等差数列， 13分 若为定值，令，则，‎ 即对恒成立，‎ 因为，问题等价于 将代入，解得.‎ 因为，所以，‎ 所以，又故. 16分 ‎20. 解（1）当时，‎ 当时，，则，‎ 令，解得或（舍），所以时，， ‎ 所以函数在区间上为减函数. 2分 当时，，，‎ 令，解得，当时，，当时，，‎ 所以函数在区间上为减函数，在区间上为增函数， 且. 4分 综上，函数的单调减区间为和，单调增区间为． 5分 ‎（注：将单调减区间为和写出的扣1分）‎ ‎（2）设，则，所以，‎ 由题意，在区间上有解，‎ 等价于在区间上有解. 6分 记，‎ 则， 7分 令，因为，所以，故解得，‎ 当时，，当时，，‎ 所以函数在区间上单调递减，在区间上单调递增，‎ 故函数在处取得最小值. 9分 要使方程在区间上有解，当且仅当，‎ 综上，满足题意的实数a的取值范围为. 10分 ‎（3）由题意，，‎ 当时，，此时函数在上单调递增，‎ 由，可得，与条件矛盾，所以. 11分 令，解得，‎ 当时，，当时，，‎ 所以函数在上单调递减，在上单调递增.‎ 若存在，，则介于m，n之间， 12分 不妨设，‎ 因为在上单调递减，在上单调递增，且，‎ 所以当时，，‎ 由，，可得，故，‎ 又在上单调递减，且，所以．‎ 所以，同理． 14分 即解得，‎ 所以. 16分 ‎ ‎ 附加题参考答案 ‎21A 选修4－1 几何证明选讲 证明 连PB，PC，因为分别为 同弧BP上的圆周角和弦切角， 所以. 2分 因为，，‎ 所以△PDB∽△PFC，故. 5分 同理，，‎ 又，，‎ 所以△PFB∽△PEC，故. 8分 所以，即. 10分 ‎21B 选修4－2 矩阵与变换 解 矩阵的特征多项式为， 2分 令，解得，解得 属于λ1的一个特征向量为，属于λ2的一个特征向量为． 5分 令，即，所以解得．‎ ‎ 7分 所以 ‎． 10分 ‎21C 选修4－4 坐标系与参数方程 解 由曲线C的极坐标方程是，得ρ2sin2θ=2ρcosθ．‎ 所以曲线C的直角坐标方程是y2=2x． 2分 由直线l的参数方程 (t为参数)，得，‎ 所以直线l的普通方程为． 4分 将直线l的参数方程代入曲线C的普通方程y2=2x，得，‎ 设A，B两点对应的参数分别为t1，t2，‎ 所以， 7分 因为原点到直线的距离，‎ 所以△AOB的面积是． 10分 ‎21D 选修4－5 不等式选讲 解 因为a，b，c∈R，，‎ 由柯西不等式得， 4分 因为对一切实数a，b，c恒成立，‎ 所以．‎ 当时，，即；‎ 当时，不成立；‎ 当时，，即；‎ 综上，实数x的取值范围为． 10分 ‎22. 解（1）因为平面ABCD⊥平面ABEP，平面ABCD∩平面ABEPAB，BP⊥AB，‎ 所以BP⊥平面ABCD，又AB⊥BC，所以直线BA，BP，BC两两垂直， ‎ 以B为原点，分别以BA，BP，BC为x轴，y轴，z轴建立如图所示的空间直角坐标系,则P（0，2，0），B（0，0，0），D（2，0，1），E（2，1，0），C（0，0，1），‎ 因为BC⊥平面ABPE，所以为平面ABPE的一个法向量， 2分 ‎，设平面PCD的一个法向量为，‎ 则 即令，则，故， 4分 设平面PCD与平面ABPE所成的二面角为，则，‎ 显然，所以平面PCD与平面ABPE所成二面角的余弦值． 6分 ‎（2）设线段PD上存在一点N，使得直线BN与平面PCD所成角α的正弦值等于．‎ 设，． 7分 由（1）知，平面PCD的一个法向量为，‎ 所以，‎ 即，解得或（舍去）． 9分 当点N与点D重合时，直线BN与平面PCD所成角的正弦值为． 10分 ‎23. 解（1）因为，整理得，‎ 由，代入得，，‎ 所以． 2分 ‎（2）由，，可得． 3分 以下用数学归纳法证明 存在实数，，使成立．‎ ‎① 当时，显然成立． 4分 ‎② 当时，假设存在，使得成立，‎ ‎ 5分 那么，当时，‎ ‎，‎ 即当时，存在，使得成立．‎ ‎ 9分 由①，②可知，存在实数，，使对任意正整 数n恒成立． 10分