2018-2019学年湖北省宜昌县域高中协同发展共同体高二上学期期末考试数学（文）试题（解析版） 17页

‎2018-2019学年湖北省宜昌县域高中协同发展共同体高二上学期期末考试数学（文）试题 一、单选题 ‎1．直线y=2x+1在x轴和y轴上的截距之和为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由直线方程，分别令，求出对应的截距即可.‎ ‎【详解】‎ 因为，令得，令，得,‎ 所以截距之和为.‎ ‎【点睛】‎ 本题主要考查直线的截距，属于基础题型.‎ ‎2．下课以后，教室里还剩下2位男同学和1位女同学，若他们依次走出教室，则第2位走出的是女同学的概率是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】先由题意确定试验所包含的基本事件总数，再确定满足条件的基本事件数，即可求出结果.‎ ‎【详解】‎ 由题意教室里还剩下2位男同学和1位女同学，他们依次走出教室，共包含3个基本事件，‎ 第2为时女同学只有一个基本事件，所以第2位走出的是女同学的概率是.‎ ‎【点睛】‎ 本题主要考查古典概型，属于基础题型.‎ ‎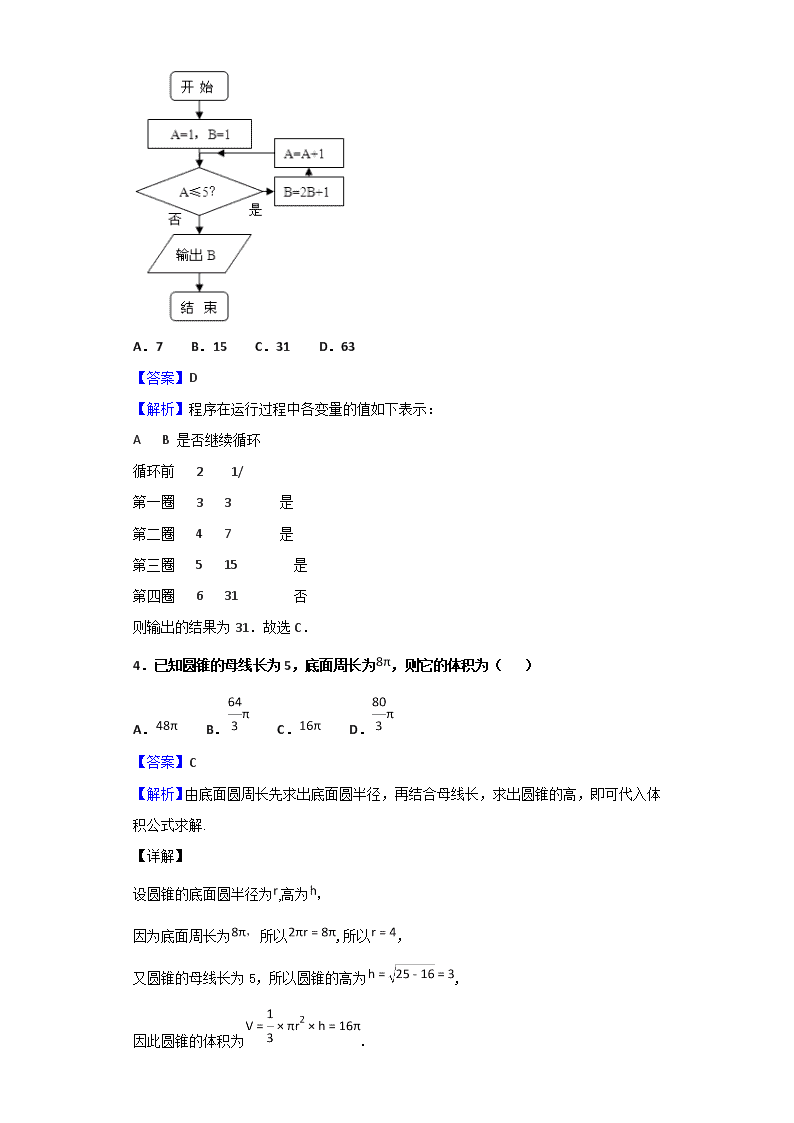3．程序框图如图所示，则该程序运行后输出的B等于(　　)‎ ‎ ‎ A．7 B．15 C．31 D．63‎ ‎【答案】D ‎【解析】程序在运行过程中各变量的值如下表示：‎ A B 是否继续循环 循环前 2 1/‎ 第一圈 3 3 是 第二圈 4 7 是 第三圈 5 15 是 第四圈 6 31 否 则输出的结果为31．故选C．‎ ‎4．已知圆锥的母线长为5，底面周长为，则它的体积为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】由底面圆周长先求出底面圆半径，再结合母线长，求出圆锥的高，即可代入体积公式求解.‎ ‎【详解】‎ 设圆锥的底面圆半径为,高为，‎ 因为底面周长为所以,所以，‎ 又圆锥的母线长为5，所以圆锥的高为,‎ 因此圆锥的体积为.‎ ‎【点睛】‎ 本题主要考查圆锥的体积，属于基础题型.‎ ‎5．小明需要从甲城市编号为1-14的14个工厂或乙城市编号为15-32的18个工厂中选择一个去实习，设“小明在甲城市实习”为事件A，“小明在乙城市且编号为3的倍数的工厂实习”为事件B，则P(A+B)=（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由题意可知A,B两事件互斥，根据互斥事件的概率公式求解即可.‎ ‎【详解】‎ 由题意可知A,B两事件互斥,且，‎ 所以.‎ ‎【点睛】‎ 本题主要考查互斥事件的概率加法公式，属于基础题型.‎ ‎6．已知直线若则实数a的值是（ ）‎ A．0 B．2或-3 C．0或3 D．3‎ ‎【答案】C ‎【解析】由直线垂直可得两直线对应系数的关系，从而可求出结果.‎ ‎【详解】‎ 因为，直线；‎ 所以，解得或.‎ ‎【点睛】‎ 本题主要考查由直线垂直求参数的值，属于基础题型.‎ ‎7．已知一组数据的平均数是2，那么另一组数据的平均数为（ ）‎ A．1 B．2 C．3 D．4‎ ‎【答案】A ‎【解析】根据平均数的计算公式可直接求解。‎ ‎【详解】‎ 因为的平均数是2，即 所以的平均数为 ‎【点睛】‎ 本题主要考查平均数的计算公式，属于基础题型.‎ ‎8．已知直线及直线截圆C所得的弦长均为，则圆C的面积是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由两平行直线间的距离公式求出圆心到直线的距离，由弦长公式求出圆的半径，由面积公式求出圆的面积.‎ ‎【详解】‎ 因为直线及直线平行，且两直线间的距离为，‎ 所以圆心到直线的距离为,‎ 设圆的半径为,‎ 因为两直线截圆所得弦长均为,‎ 所以,因此圆的面积为.‎ ‎【点睛】‎ 本题主要考查直线与圆位置关系，属于基础题型.‎ ‎9．天气预报说，在今后的三天中，每天下雨的概率都为.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：用表示下雨，从下列随机数表的第行第列的开始读取，直到读取了组数据，‎ ‎18 18 07 92 45 44 17 16 58 09 79 83 86 19 62 06 76 50 03 10 ‎ ‎55 23 64 05 05 26 62 38 97 75 34 16 07 44 99 83 11 46 32 24‎ 据此估计，这三天中恰有两天下雨的概率近似为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由题意知模拟三天恰有两天下雨的结果，观察经随机模拟产生的数据，用列举法找出表示三天中恰有两天下雨的数据，再由古典概型的概率公式即可求解.‎ ‎【详解】‎ 由题意知模拟三天恰有两天下雨的结果，观察经随机模拟产生的数据可得，表示三天中恰有两天下雨的数据有：4 17，3 86，19 6，2 06，共4组数据，‎ 所以这三天中恰有两天下雨的概率.‎ ‎【点睛】‎ 本题主要考查模拟方法估计概率，属于基础题型.‎ ‎10．某种商品的广告费支出x与销售额y（单位：万元）之间有如下对应数据，根据表中提供的数据，得出y与x的线性回归方程为，则表中的m的值为（ ）‎ x ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎30‎ ‎40‎ m ‎50‎ ‎70‎ A．45 B．50 C．55 D．60‎ ‎【答案】D ‎【解析】由表中数据，计算. 平均值为=1 5 ×（2+4+5+6+8）=5，‎ ‎=1 5×（30+40+50+m+70）=38+，‎ ‎∵回归直线方程y =6.5x+17.5过样本中心，‎ ‎∴38+m 5 =6.5×5+17.5，‎ 解得m=60．‎ 故选：D．‎ ‎11．如图，椭圆的左、右焦点分别为，过椭圆上的点作轴的垂线，垂足为，若四边形为菱形，则该椭圆的离心率为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】先由题意得到的坐标，再由四边形为菱形求出点坐标，代入椭圆方程即可求解.‎ ‎【详解】‎ 由题意，,‎ 因为四边形为菱形，所以,‎ 将点坐标代入可得：，整理得，‎ 所以，因,故解方程得，.‎ ‎【点睛】‎ 本题主要考查椭圆的简单性质，属于基础题型.‎ ‎12．小华爱好玩飞镖，现有如图所示的由两个边长都为的正方形和构成的标靶图形，如果点正好是正方形的中心，而正方形可以绕点旋转，则小华随机向标靶投飞镖射中阴影部分的概率是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】先连OA,OB，设OR交BC于M,OP交AB于N，由四边形 是正方形，得到，再由四边形为正方形，可证，从而可求出结果.‎ ‎【详解】‎ 先连OA,OB，设OR交BC于M,OP交AB于N,如图所示：‎ 因为四边形是正方形，所以，‎ 又四边形为正方形，所以，‎ 所以，‎ 所以，即它们重叠部分的面积为1，总面积是7，‎ 故小华随机向标靶投飞镖射中阴影部分的概率是.‎ ‎【点睛】‎ 本题主要考查与面积有关的几何概型，属于基础题型.‎ 二、填空题 ‎13．抛物线的准线方程是____________‎ ‎【答案】‎ ‎【解析】先将抛物线方程化为标准方程，即可求解.‎ ‎【详解】‎ 由，所以，故准线方程为.‎ ‎【点睛】‎ 本题主要考查抛物线的简单性质，属于基础题型.‎ ‎14．已知命题,使得是假命题，则实数的最大值是____________‎ ‎【答案】‎ ‎【解析】由命题“，使得”是假命题，得“，使得”是真命题，从而可求出结果.‎ ‎【详解】‎ 因为命题“，使得”是假命题，‎ 所以“，使得”是真命题，‎ 故.‎ ‎【点睛】‎ 本题主要考查根据命题真假判断参数的范围，属于基础题型.‎ ‎15．经过两点，且圆心在x轴上的圆C的标准方程为____________‎ ‎【答案】‎ ‎【解析】由圆心在x轴上，先设圆的方程为，再由圆过点,列方程组，求解即可.‎ ‎【详解】‎ 因为圆心在x轴上，所以设圆的方程为，又圆过点，‎ 所以有，解得，所以圆的方程为.‎ ‎【点睛】‎ 本题主要考查待定系数法求圆的方程，属于基础题型.‎ ‎16．为调查一单位落实“中央某项规定”情况，采用系统抽样方法从该单位480人中抽取32人做问卷调查，将他们随机编号为1,2，…，480，分组后在第一组采用简单随机抽样的方法抽到的号码为3。抽到的32人中，编号落入区间[1，225]的人做问卷A，编号落入区间[226，380]的人做问卷B，其余的人做问卷C，做问卷C的人数为____________‎ ‎【答案】‎ ‎【解析】先由题意得出组距，设做问卷A，B，C的人数，列不等式组求出A，B的人数，即可求解.‎ ‎【详解】‎ 由题意可得，组距,因为第一组抽到的号码为3，所以做问卷A,B,C的有m,n,t 人，‎ 则有，解得，所以人.‎ ‎【点睛】‎ 本题主要考查系统抽样，属于基础题型.‎ 三、解答题 ‎17．某学校900名学生在一次百米测试中，成绩全部介于13秒与18 秒之间，利用分层抽样的方法抽取其中若干个样本，将测试结果按如下方式分成五组：第一组[13,14），第二组[14,15），…，第五组[17,18]，有关数据见下表：‎ 各组组员数 各组抽取人数 ‎[13,14）‎ ‎ 54‎ a ‎[14,15）‎ b ‎8‎ ‎[15,16）‎ ‎342‎ ‎19‎ ‎[16,17）‎ ‎288‎ c ‎[17,18]‎ ‎ ‎ d ‎（1）求a,b,c,d的值；‎ ‎（2）若样本第一组中只有一个女生，其他都是男生，第五组则只有一个男生，其他都是女生，现从第一、五组中各抽一个同学组成一个新的组，求这个新组恰好由一个男生和一个女生构成的概率。‎ ‎【答案】（1）的值分别为（2）‎ ‎【解析】(1)利用频率表中的概率之和为1，利用频数除以频率等于样本容量求出的值即可；‎ ‎(2)列举出所有的基本事件，再找到满足条件的基本事件，根据概率公式计算即可；‎ ‎【详解】‎ 解：(1)因为，所以每个学生被抽到的概率都为 故 故的值分别为 ‎(2)样本中第一组共有3人，第五组共有4人。‎ 其中第五组四人记为a、b、c、d，其中a为男生，b、c、d为女生，第一组三人记为1、2、3，其中1、2为男生，3为女生，基本事件列表如下：‎ a b c d ‎1‎ ‎1a ‎1b ‎1c ‎1d ‎2‎ ‎2a ‎1b ‎2c ‎2d ‎3‎ ‎3a ‎3b ‎3c ‎3d 所以基本事件有12个，‎ 恰为一男一女的事件有1b，1c，1d，2b，2c，2d，3a共7个，‎ 因此新组恰由一男一女构成的概率是 ‎【点睛】‎ 本题主要考查古典概型及其概率计算公式，属于基础题型.‎ ‎18．青少年“心理健康”问题越来越引起社会关注，某校对高一600名学生进行了一次“心理健康”知识测试，并从中抽取了部分学生的成绩（得分取正整数，满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图。‎ 分组 频数 频率 ‎[50,60）‎ ‎2‎ ‎0.04‎ ‎[60,70）‎ ‎8‎ ‎0.16‎ ‎[70,80）‎ ‎10‎ ‎[80,90）‎ ‎[90,100]‎ ‎14‎ ‎0.28‎ 合计 ‎1.00‎ ‎ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎（1）填写答题卡频率分布表中的空格，补全频率分布直方图，并标出每个小矩形对应的纵轴数据； ‎ ‎（2）请你估算学生成绩的平均数及中位数。‎ ‎【答案】（1）详见解析（2）平均数81.4，中位数83.125‎ ‎【解析】(1)先求出样本容量，再计算表中所缺的频率与频数，完成频率分布表与频率分布直方图；‎ ‎(2)结合频率分布直方图求解即可.‎ ‎【详解】‎ 解：(1) ‎ ‎　 ‎ ‎(2)设所求平均数为，由频率分布直方图可得：‎ 所以学生成绩的平均分数约为81.4(分)‎ 设中位数为X,依题意得 解得 ‎【点睛】‎ 本题主要考查频率分布表与频率分布直方图，属于基础题型.‎ ‎19．为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响，某校课外兴趣小组记录了组昼夜温差与颗种子发芽数，得到如下资料：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 温差（）‎ ‎10‎ ‎11‎ ‎13‎ ‎12‎ ‎8‎ 发芽数（颗）‎ ‎23‎ ‎25‎ ‎30‎ ‎26‎ ‎16‎ 经分析，这组数据具有较强的线性相关关系，因此该小组确定的研究方案是：先从这五组数据中选取组数据求出线性回归方程，再用没选取的组数据进行检验.‎ ‎（1）若选取的是第组的数据，求出关于的线性回归方程；‎ ‎（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？‎ ‎（参考公式：，）‎ ‎【答案】（1）（2）可靠 ‎【解析】(1)根据所给的数据,先做出的平均数，即做出本组数据的样本中心点，根据最小二乘法求出线性回归方程的系数,写出线性回归方程；(2)‎ 根据估计数据与所选出的检验数据的误差均不超过2颗,就认为得到的线性回归方程是可靠的，根据求得的结果和所给的数据进行比较，得到所求的方程是可靠的.‎ ‎【详解】‎ ‎（1）由题意：，,‎ ‎．‎ ‎，‎ 故回归直线方程为：．‎ ‎(2)当时，，‎ 当时，，所以（1）中所得的回归直线方程是可靠的.‎ ‎【点睛】‎ 本题主要考查线性回归方程的求解与应用，属于中档题.求回归直线方程的步骤：①依据样本数据确定两个变量具有线性相关关系；②计算的值；③计算回归系数；④写出回归直线方程为； 回归直线过样本点中心是一条重要性质，利用线性回归方程可以估计总体，帮助我们分析两个变量的变化趋势.‎ ‎20．在如图所示的五面体中，四边形是矩形，平面平面，且, ，， ，点在上.‎ ‎ 求证：（1）平面 ‎（2）平面 平面 ‎【答案】详见解析 ‎【解析】(1)先证明平面平面,进而由面面平行可得线面平行；‎ ‎(2)利用勾股定理的逆定理证明直线,由面面垂直的性质得到平面,进而可得平面，从而可得平面 平面.‎ ‎【详解】‎ 证明：（1）连结DM ‎∵AB∥EF，AB=EF，M是EF的中点，‎ ‎∴AB∥EM且ABEM,四边形ABEM是平行四边形，‎ ‎∴AM∥BE，又∵AM⊄平面BCE，BE⊂平面BCE，‎ ‎∴AM∥平面BCE．∵四边形ABCD是矩形，‎ ‎∴AD∥BC，又BC⊂平面BCE，AD⊄平面BCE，∴AD∥平面BCE，‎ 又AD⊂平面ADM，AM⊂平面ADM，AD∩AM=A，‎ ‎∴平面ADM∥平面BCE，‎ 又DN⊂平面ADM， ‎ ‎∴DN∥平面BCE（2）由（1）知AM=BE=2，‎ ‎∵AF=BE=2，MF=EF=‎ ‎∴AM2+AF2=MF2，∴AM⊥AF．‎ ‎∵平面ADF⊥平面ABEF，平面ADF∩平面ABEF=AF，AM⊂平面ABEF，‎ ‎∴AM⊥平面DAF，∵DA⊂平面DAF，‎ ‎∴AM⊥DA，‎ 又∵四边形ABCD是矩形，∴AD⊥AB，‎ ‎∵AB⊂平面ABEF，AM⊂平面ABEF，AB∩AM=A，‎ ‎∴AD⊥平面ABEF，又AD⊂平面ABCD，‎ ‎∴平面ABEF⊥平面ABCD ‎【点睛】‎ 本题主要考查线面平行的判定与性质，以及面面垂直的判定与性质，属于基础题型.‎ ‎21．已知圆的方程为，直线的方程为，点在直线上.‎ ‎（1）若点的坐标为，过点作圆的割线交圆于两点，当 时，求直线的方程；.‎ ‎（2）若过点作圆的切线，切点为，求证：经过四点的圆必过定点，并求出所有定点的坐标.‎ ‎【答案】（1）或；（2）过定点 ‎【解析】(1)依题意，先设直线方程y−2=k(x-1)，由点到直线距离公式即可求解;‎ ‎(2)先由条件得到圆心坐标，写出圆的标准方程，化简整理，由圆的方程即可求出结果.‎ ‎【详解】‎ 解：(1)依题意，割线CD的斜率一定存在，设为k,则其方程为：y−2=k(x-1)，‎ 即kx-y+2−k=0.‎ 则圆心到直线的距离，且 ‎∴直线CD的方程为： ‎ ‎(2)由条件可知四点在以为直径的圆上，设 又则的中点为所以经过四点的圆的方程为 化简得 由解得 或 于是经过四点的圆必过定点 ‎【点睛】‎ 本题主要考查直线的方程与圆过定点问题，属于基础题型.‎ ‎22．已知椭圆过两点，过点的动直线与椭圆交于两点 ‎ (1) 求椭圆的标准方程； ‎ ‎ (2)当时，求直线的方程.‎ ‎【答案】（1）（2）或 ‎【解析】(1)将代入椭圆方程得到方程组，解方程组即可；‎ ‎(2)先设，由得到与关系式①，再由直线与曲线方程联立与①即可求出结果，但要注意斜率不存在的情况.‎ ‎【详解】‎ 解：（1）将点代入椭圆，得 故椭圆的标准方程为 ‎ (2)设，①‎ 若直线的斜率存在，可设 则由得 与①联立解得 若直线的斜率不存在，则 综上可知，直线的方程为，即或 ‎【点睛】‎ 本题主要考查椭圆的方程和椭圆的简单性质，属于中档试题.‎