高考文科数学专题复习练习3三视图与直观图 20页

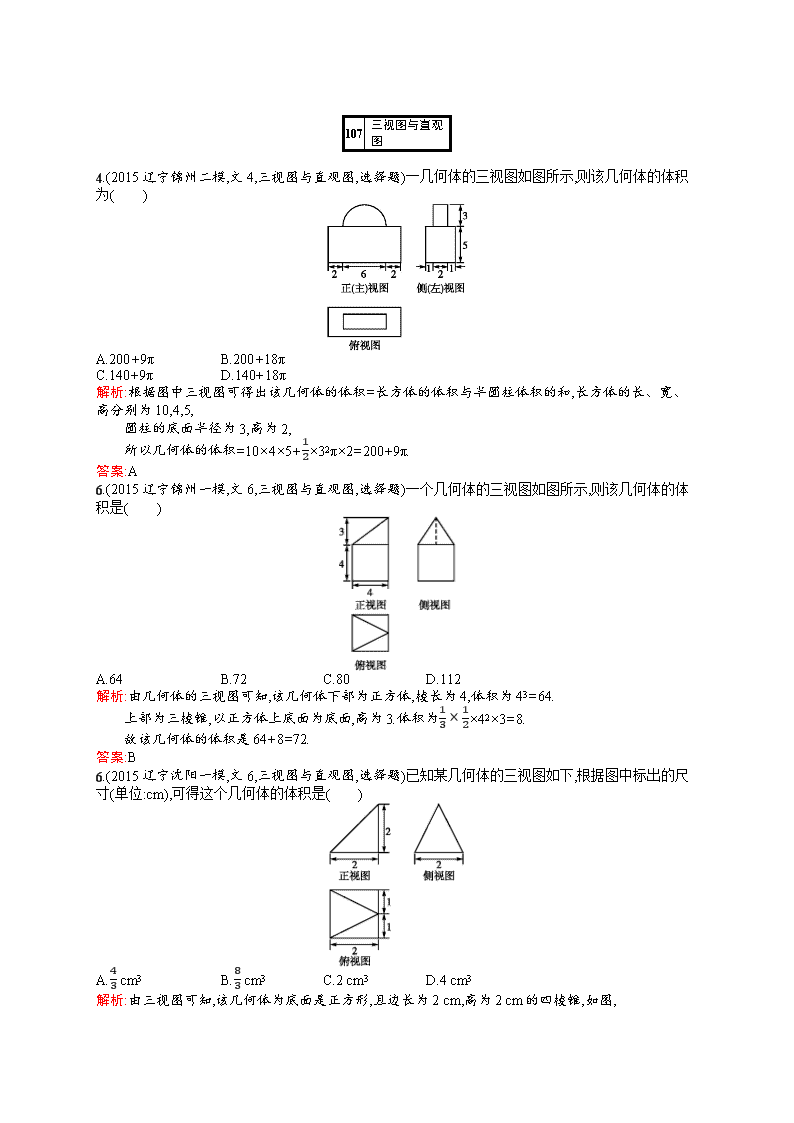
‎107‎ 三视图与直观图 ‎4.(2015辽宁锦州二模,文4,三视图与直观图,选择题)一几何体的三视图如图所示,则该几何体的体积为(　　)‎ A.200+9π B.200+18π C.140+9π D.140+18π 解析:根据图中三视图可得出该几何体的体积=长方体的体积与半圆柱体积的和,长方体的长、宽、高分别为10,4,5,‎ 圆柱的底面半径为3,高为2,‎ 所以几何体的体积=10×4×5+‎1‎‎2‎×32π×2=200+9π.‎ 答案:A ‎6.(2015辽宁锦州一模,文6,三视图与直观图,选择题)一个几何体的三视图如图所示,则该几何体的体积是(　　)‎ A.64 B.72 C.80 D.112‎ 解析:由几何体的三视图可知,该几何体下部为正方体,棱长为4,体积为43=64.‎ 上部为三棱锥,以正方体上底面为底面,高为3.体积为‎1‎‎3‎‎×‎‎1‎‎2‎×42×3=8.‎ 故该几何体的体积是64+8=72.‎ 答案:B ‎6.(2015辽宁沈阳一模,文6,三视图与直观图,选择题)已知某几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是(　　)‎ A.‎4‎‎3‎ cm3 B.‎8‎‎3‎ cm3 C.2 cm3 D.4 cm3‎ 解析:由三视图可知,该几何体为底面是正方形,且边长为2 cm,高为2 cm的四棱锥,如图,‎ 故V=‎1‎‎3‎×22×2=‎8‎‎3‎(cm3).‎ 答案:B ‎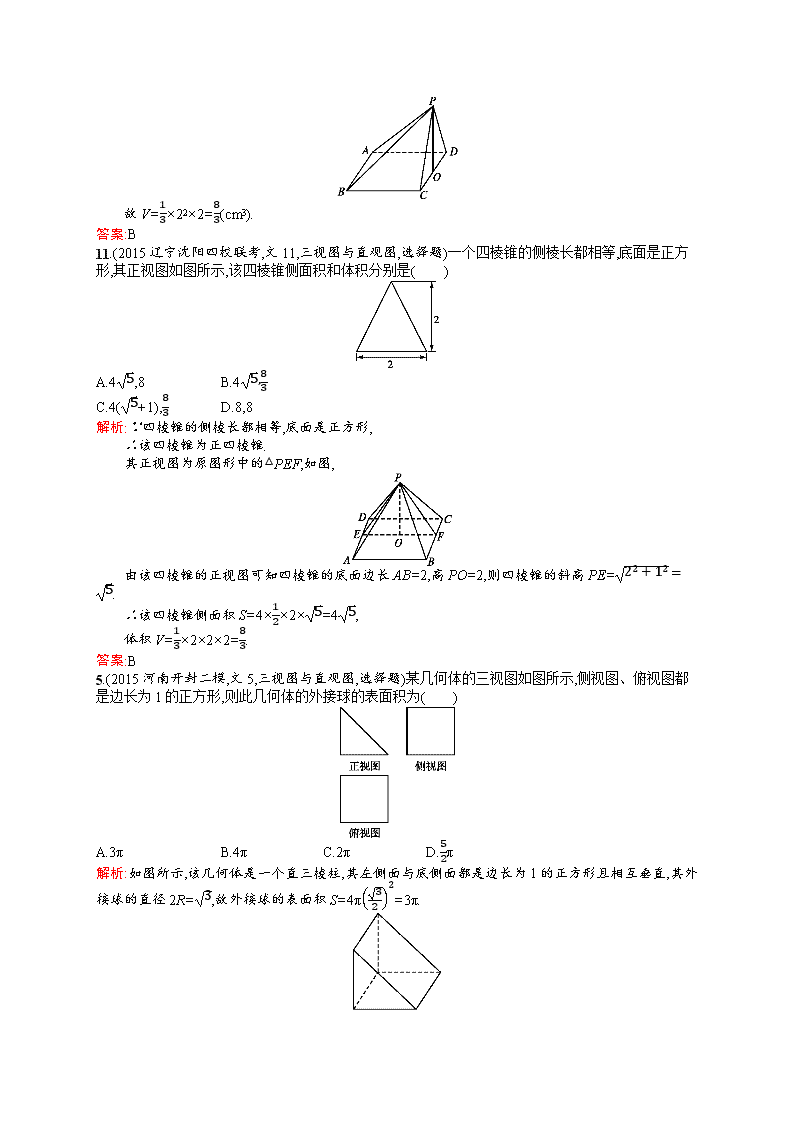11.(2015辽宁沈阳四校联考,文11,三视图与直观图,选择题)一个四棱锥的侧棱长都相等,底面是正方形,其正视图如图所示,该四棱锥侧面积和体积分别是(　　)‎ A.4‎5‎,8 B.4‎‎5‎‎,‎‎8‎‎3‎ C.4(‎5‎+1),‎8‎‎3‎ D.8,8‎ 解析:∵四棱锥的侧棱长都相等,底面是正方形,‎ ‎∴该四棱锥为正四棱锥.‎ 其正视图为原图形中的△PEF,如图,‎ 由该四棱锥的正视图可知四棱锥的底面边长AB=2,高PO=2,则四棱锥的斜高PE=‎2‎‎2‎‎+‎‎1‎‎2‎‎=‎‎5‎.‎ ‎∴该四棱锥侧面积S=4×‎1‎‎2‎×2×‎5‎=4‎5‎,‎ 体积V=‎1‎‎3‎×2×2×2=‎8‎‎3‎.‎ 答案:B ‎5.(2015河南开封二模,文5,三视图与直观图,选择题)某几何体的三视图如图所示,侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为(　　)‎ A.3π B.4π C.2π D.‎5‎‎2‎π 解析:如图所示,该几何体是一个直三棱柱,其左侧面与底侧面都是边长为1的正方形且相互垂直,其外接球的直径2R=‎3‎,故外接球的表面积S=4π‎3‎‎2‎‎2‎=3π.‎ 答案:A ‎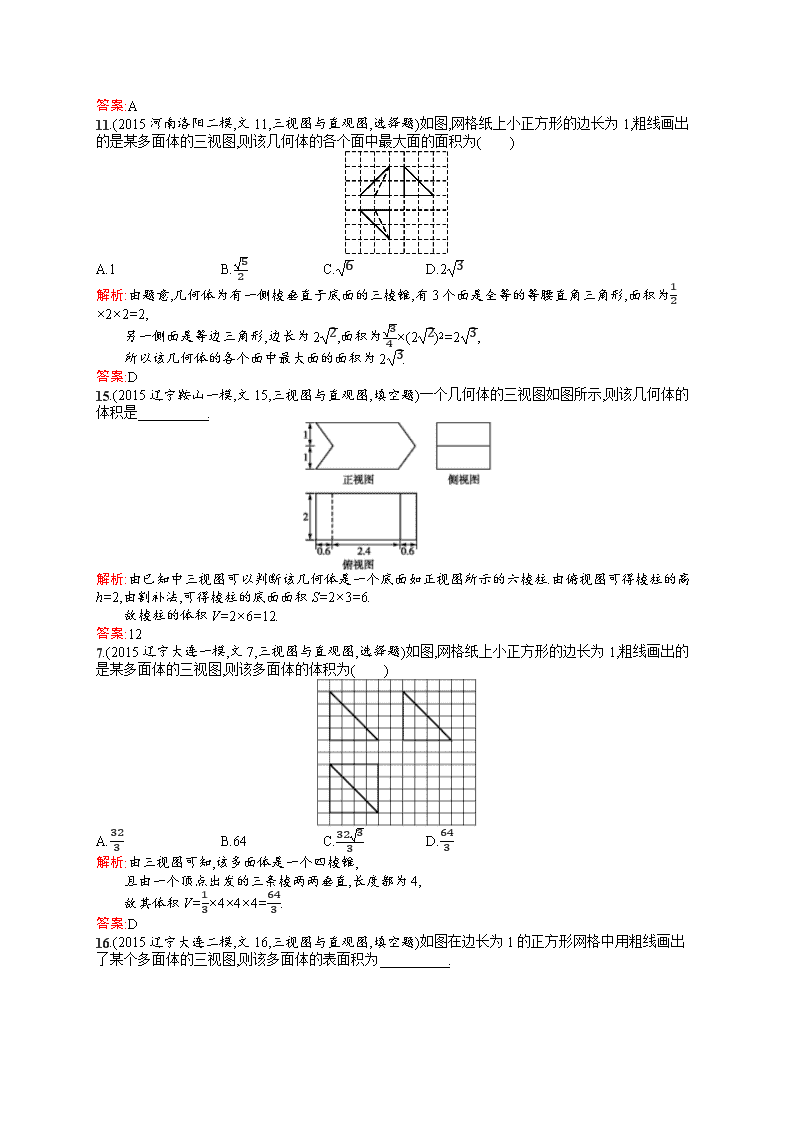11.(2015河南洛阳二模,文11,三视图与直观图,选择题)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为(　　)‎ A.1 B.‎5‎‎2‎ C.‎6‎ D.2‎‎3‎ 解析:由题意,几何体为有一侧棱垂直于底面的三棱锥,有3个面是全等的等腰直角三角形,面积为‎1‎‎2‎×2×2=2,‎ 另一侧面是等边三角形,边长为2‎2‎,面积为‎3‎‎4‎×(2‎2‎)2=2‎3‎,‎ 所以该几何体的各个面中最大面的面积为2‎3‎.‎ 答案:D ‎15.(2015辽宁鞍山一模,文15,三视图与直观图,填空题)一个几何体的三视图如图所示,则该几何体的体积是　　　　　. ‎ 解析:由已知中三视图可以判断该几何体是一个底面如正视图所示的六棱柱.由俯视图可得棱柱的高h=2,由割补法,可得棱柱的底面面积S=2×3=6.‎ 故棱柱的体积V=2×6=12.‎ 答案:12‎ ‎7.(2015辽宁大连一模,文7,三视图与直观图,选择题)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为(　　)‎ A.‎32‎‎3‎ B.64 C.‎32‎‎3‎‎3‎ D.‎‎64‎‎3‎ 解析:由三视图可知,该多面体是一个四棱锥,‎ 且由一个顶点出发的三条棱两两垂直,长度都为4,‎ 故其体积V=‎1‎‎3‎×4×4×4=‎64‎‎3‎.‎ 答案:D ‎16.(2015辽宁大连二模,文16,三视图与直观图,填空题)如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的表面积为　　　　　. ‎ 解析:根据几何体的三视图,得 该几何体是底面为等腰直角三角形的三棱锥P-ABC,且三棱锥的高PO=2,如图所示:‎ ‎∴侧面△PAB的面积为S△PAB=‎1‎‎2‎×4‎2‎×2=4‎2‎,‎ ‎△PBC与△PAC的面积为S△PBC=S△PAC=‎1‎‎2‎×4×‎2‎‎2‎‎+‎‎2‎‎2‎=4‎2‎,‎ 底面△ABC的面积为S△ABC=‎1‎‎2‎×4×4=8.‎ ‎∴三棱锥的表面积为S△PAB+S△PAC+S△PBC+S△ABC=8+12‎2‎.‎ 答案:8+12‎‎2‎ ‎9.(2015河南六市联考一模,文9,三视图与直观图,选择题)一个几何体的三视图如图所示,则这个几何体的体积是(　　)‎ A.1 B.2 C.3 D.4‎ 解析:根据几何体的三视图,得 该几何体是如图所示的四棱锥P-ABCD,‎ 且底面为直角梯形ABCD,高为2.‎ 故该四棱锥的体积为V=‎1‎‎3‎‎×‎‎1‎‎2‎×(2+4)×2×2=4.‎ 答案:D ‎7.(2015河南开封定位模拟,文7,三视图与直观图,选择题)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是(　　)‎ A.108 cm3 B.100 cm3 C.92 cm3 D.84 cm3‎ 解析:根据几何体的三视图知,该几何体是长为6,宽为3,高为6的长方体,去掉一个底面直角边长为4和3,高为4的三棱锥,‎ 可知该几何体的体积是V=V长方体-V三棱锥=6×3×6-‎1‎‎3‎‎×‎‎1‎‎2‎×4×3×4=100(cm3).‎ 答案:B ‎10.(2015天津河北区一模,文10,三视图与直观图,填空题)一个几何体的三视图如图所示,则该几何体的体积为　　　　　. ‎ 解析:由三视图知几何体为半圆柱和直三棱柱,半圆柱的半径为2,高为3,体积为6π;直三棱柱的底面为直角三角形,面积为4,高为3,体积为12.故几何体的体积为6π+12.‎ 答案:6π+12‎ ‎8.(2015河南中原名校联盟模拟,文8,三视图与直观图,选择题)如图,某几何体的正视图与侧视图都是边长为1的正方形,且其体积为π‎4‎.则该几何体的俯视图可以是(　　)‎ 解析:根据正视图与侧视图的形状和几何体的体积是π‎4‎,‎ 知该几何体的底面积是π‎4‎,‎ 故底面可以是一个半径为1的四分之一圆.‎ 答案:D ‎108‎ 空间几何体的表面积 ‎7.(2015辽宁重点中学协作体模拟,文7,空间几何体的表面积,选择题)某几何体的三视图如图所示,则此几何体的表面积为(　　)‎ A.‎140‎‎3‎π+4‎13‎π B.36π+2‎13‎π C.32π+2‎13‎π D.44π+2‎13‎π 解析:根据三视图得知,‎ 该几何体是由下面是一个半径为4的半球,上面是一个底面半径为2,高为3的圆锥构成的组合体.‎ 首先求出上面圆锥的侧面展开图的半径r=‎13‎,‎ 圆锥的底面周长为l=4π,‎ 所以圆锥的侧面面积为:S1=‎1‎‎2‎·4π·‎13‎=2‎13‎π,‎ 剩余的侧面面积为:S2=2π·16+16π-4π=44π,‎ 所以组合体的侧面面积为:S=S1+S2=44π+2‎13‎π.‎ 答案:D ‎15.(2015河南洛阳二模,文15,空间几何体的表面积,填空题)已知点A,B,C,D均在球O上,AB=BC=‎6‎,AC=2‎3‎,若三棱锥D-ABC体积的最大值为3,则球O的表面积为　　　　　. ‎ 解析:∵AB=BC=‎6‎,AC=2‎3‎,‎ ‎∴AB⊥BC,S△ABC=3.‎ ‎∵三棱锥D-ABC的体积的最大值为3,‎ ‎∴D到平面ABC的最大距离为3.‎ 设球的半径为R,则(‎3‎)2=3×(2R-3),‎ ‎∴R=2,∴球O的表面积为4πR2=16π.‎ 答案:16π ‎9.(2015宁夏银川一中一模,文9,空间几何体的表面积,选择题)一个几何体的三视图如图所示,则该几何体的外接球的表面积为(　　)‎ A.36π B.8π C.‎9‎‎2‎π D.‎27‎‎8‎π 解析:根据几何体的三视图,得 该几何体是底面为等腰直角三角形,高为2的直三棱锥,‎ 如图所示,‎ 则该直三棱锥的外接球是对应直三棱柱的外接球,‎ 设几何体外接球的半径为R,‎ ‎∵底面是等腰直角三角形,‎ ‎∴底面外接圆的半径为1.‎ ‎∴R2=1+1=2.‎ ‎∴外接球的表面积是4πR2=8π.‎ 答案:B ‎109‎ 空间几何体的体积 ‎14.(2015辽宁锦州一模,文14,空间几何体的体积,填空题)在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,△ABC,△ACD,△ADB的面积分别为‎2‎‎2‎‎,‎3‎‎2‎,‎‎6‎‎2‎,则三棱锥A-BCD的外接球的体积为　　　　　. ‎ 解析:三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,补成长方体,两者的外接球是同一个,长方体的对角线就是球的直径,‎ 设长方体的长、宽、高分别为a,b,c,则由题意,得 ab=‎6‎,ac=‎3‎,bc=‎2‎,‎ 解得a=‎3‎,b=‎2‎,c=1.‎ 所以球的直径为‎3+2+1‎‎=‎‎6‎,球的半径为‎6‎‎2‎.‎ 故三棱锥A-BCD的外接球的体积为‎4‎‎3‎π×‎6‎‎2‎‎3‎‎=‎‎6‎π.‎ 答案:‎6‎π ‎16.(2015辽宁重点中学协作体模拟,文16,空间几何体的体积,填空题)如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD.若∠BPC=90°,PB=‎2‎,PC=2,则四棱锥P-ABCD体积的最大值为　　　　　. ‎ 解析:如图所示,作PO⊥AD,垂足为O,作OG⊥BC,垂足为G,连接GP.‎ ‎∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,∴PO⊥平面ABCD.‎ 在△BPC中,∵∠BPC=90°,PB=‎2‎,PC=2,‎ ‎∴BC=BP‎2‎+PC‎2‎‎=‎‎6‎.‎ ‎∴PG=BP·PCBC‎=‎‎2‎‎3‎‎3‎.‎ 设AB=x,则OG=x,‎ PO=PG‎2‎-OG‎2‎‎=‎‎4‎‎3‎‎-‎x‎2‎,‎ ‎∴VP-ABCD=‎1‎‎3‎PO·S四边形ABCD=‎1‎‎3‎‎4‎‎3‎‎-‎x‎2‎‎×‎‎6‎x,‎ ‎∴V2=‎2‎‎3‎‎4‎‎3‎‎-‎x‎2‎x2≤‎2‎‎3‎‎4‎‎3‎‎-x‎2‎+‎x‎2‎‎2‎‎2‎‎=‎‎2‎‎3‎‎3‎,当且仅当x=‎6‎‎3‎时取等号.‎ ‎∴VP-ABCD≤‎2‎‎6‎‎9‎,即四棱锥P-ABCD体积的最大值为‎2‎‎6‎‎9‎.‎ 答案:‎‎2‎‎6‎‎9‎ ‎110‎ 组合体的“接”“切”综合问题 ‎14.(2015辽宁沈阳四校联考,文14,组合体的“接”“切”综合问题,填空题)在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=BC=‎2‎,PA=2,则此三棱锥外接球的体积为　　　　　. ‎ 解析:∵PC是Rt△PAC和Rt△PBC的公共的斜边,‎ 记它的中点为O,则OA=OB=OP=OC=‎1‎‎2‎PC=‎2‎,‎ 即该三棱锥的外接球球心为O,半径为‎2‎,‎ 故它的体积为‎4‎‎3‎π·(‎2‎)3=‎8‎‎2‎‎3‎π.‎ 答案:‎8‎‎2‎‎3‎π ‎16.(2015辽宁大连一模,文16,组合体的“接”“切”综合问题,填空题)如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为‎4‎‎2‎‎3‎,则该半球的体积为　　　　　. ‎ 解析:设球的半径为R,则底面ABCD的面积为2R2,‎ ‎∵半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为‎4‎‎2‎‎3‎,‎ ‎∴‎1‎‎3‎×2R2×R=‎4‎‎2‎‎3‎,‎ ‎∴R3=2‎2‎,‎ ‎∴该半球的体积为V=‎1‎‎2‎‎×‎‎4‎‎3‎R3π=‎4‎‎2‎‎3‎π.‎ 答案:‎4‎‎2‎‎3‎π.‎ ‎11.(2015辽宁大连二模,文11,组合体的“接”“切”综合问题,选择题)已知三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC=‎3‎AB,若三棱锥P-ABC的体积为‎3‎‎2‎,则该三棱锥的外接球的体积为(　　)‎ A.8‎3‎π B.6‎3‎π C.4‎3‎π D.2‎3‎π 解析:如图所示,‎ ‎∵三棱锥P-ABC的外接球的球心O在AB上,且PO⊥平面ABC,‎ ‎∴PO是三棱锥P-ABC的高,OA=OB=OC=OP=x,‎ ‎∴∠ACB=90°,∴AC⊥BC.‎ ‎∵2AC=‎3‎AB,∴∠ABC=60°,‎ ‎∴BC=x,AC=‎3‎x.‎ ‎∴VP-ABC=‎1‎‎3‎·S△ABC·PO=‎1‎‎3‎‎×‎1‎‎2‎×‎‎3‎x2×x=‎3‎‎2‎,解得x=‎3‎.‎ ‎∴该三棱锥的外接球的体积V=‎4π‎3‎x3=4‎3‎π.‎ 答案:C ‎14.(2015河南六市联考一模,文14,组合体的“接”“切”综合问题,填空题)已知三棱锥P-ABC的所有棱长都等于1,则三棱锥P-ABC的内切球的表面积为　　　　　. ‎ 解析:∵三棱锥P-ABC的所有棱长都等于1,‎ ‎∴底面外接圆的半径为‎3‎‎3‎.‎ ‎∴三棱锥P-ABC的高为‎1-‎‎1‎‎3‎‎=‎‎6‎‎3‎.‎ ‎∵三棱锥P-ABC的外接球与内切球的半径的比为3∶1,‎ ‎∴三棱锥P-ABC的内切球的半径为‎6‎‎12‎.‎ ‎∴三棱锥P-ABC的内切球的表面积为4π×‎6‎‎12‎‎2‎‎=‎π‎6‎.‎ 答案:‎π‎6‎ ‎8.(2015哈尔滨师大附中、东北师大附中、辽宁省实验中学一模,文8,组合体的“接”“切”综合问题,选择题)半径为1的球面上有四个点A,B,C,D,球心为点O,AB过点O,CA=CB,DA=DB,DC=1,则三棱锥A-BCD的体积为(　　)‎ A.‎3‎‎6‎ B.‎3‎‎3‎ C.‎3‎ D.‎‎6‎ 解析:由题意可知图形如图,AB过点O,CA=CB,DA=DB,三角形ABD与ACB都是等腰直角三角形,‎ 半径为1的球面上有四个点A,B,C,D,球心为点O,‎ ‎∴AD=BD=AC=BC=‎2‎,DC=1,OD=OC=1,AB⊥OD,AB⊥OC.‎ ‎∴三棱锥A-BCD的体积为‎1‎‎3‎‎×‎‎1‎‎2‎S△OCD·(AO+OB)=‎1‎‎3‎‎×‎‎3‎‎4‎×12×2=‎3‎‎6‎.‎ 答案:A ‎11.(2015河南商丘二模,文11,组合体的“接”“切”综合问题,选择题)设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为(　　)‎ A.πa2 B.‎7‎‎3‎πa2 C.‎11‎‎3‎πa2 D.5πa2‎ 解析:根据题意条件可知三棱柱是棱长都为a的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为R=a‎2‎‎2‎‎+‎a‎2sin60°‎‎2‎‎=‎‎7‎‎12‎a‎2‎,‎ 球的表面积为S=4π·‎7‎a‎2‎‎12‎‎=‎‎7‎‎3‎πa2.‎ 答案:B ‎112‎ 空间两条直线的位置关系 ‎3.(2015辽宁重点中学协作体模拟,文3,空间两条直线的位置关系,选择题)已知平面α及空间中的任意一条直线a,那么在平面α内一定存在直线b使得(　　)‎ A.a∥b B.a与b相交 C.a与b是异面直线 D.a⊥b 解析:当直线a与平面α相交时,平面α内的任意一条直线与直线a的关系只有两种:异面、相交,此时就不可能平行了,故A错.‎ 当直线a与平面α平行时,平面α内的任意一条直线与直线a的关系只有两种:异面、平行,此时就不可能相交了,故B错.‎ 当直线a在平面α内时,平面α内的任意一条直线与直线a的关系只有两种:平行、相交,此时就不可能异面了,故C错.‎ 不管直线a与平面α的位置关系相交、平行,还是在平面内,都可以在平面α内找到一条直线与直线b垂直,因为直线在异面与相交时都包括垂直的情况,故D正确.‎ 答案:D ‎19.(2015河南开封二模,文19,空间两条直线的位置关系,解答题)如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.‎ ‎(1)求证:AC⊥BB1;‎ ‎(2)若P是棱B1C1的中点,求平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比.‎ ‎(1)证明:在三棱柱ABC-A1B1C1中,‎ ‎∵A1B⊥平面ABC,A1B⊂平面ABB1,‎ ‎∴平面ABB1A1⊥平面ABC.‎ ‎∵平面ABB1A1∩平面ABC=AB,AB⊥AC,‎ ‎∴AC⊥平面ABB1A1,‎ ‎∴AC⊥BB1.‎ ‎(2)解:设平面PAB与棱A1C1交于Q,‎ ‎∵P为棱B1C1的中点,‎ ‎∴Q为棱A1C1的中点,‎ 连接AQ,PQ,设三棱柱ABC-A1B1C1的底面积为S,高为h,体积为V,‎ 则Sh=V,如图,将棱台C1PQ-ABC还原为棱锥S-ABC,解得VPQC‎1‎-ABC‎=‎‎7‎‎12‎V,‎ VAB-A‎1‎B‎1‎PQ‎=V-‎7‎‎12‎V=‎5‎‎12‎V.‎ ‎∴平面PAB将三棱柱ABC-A1B1C1分成的两部分体积之比为VPQC‎1‎-ABCVAB-A‎1‎B‎1‎PQ‎=‎‎7‎‎5‎.‎ ‎4.(2015辽宁鞍山一模,文4,空间两条直线的位置关系,选择题)已知空间中不共面的四点A,B,C,D及平面α,下列说法正确的是(　　)‎ A.直线AB,CD可能平行 B.直线AB,CD可能相交 C.直线AB,CD可能都与α平行 D.直线AB,CD可能都与α垂直 解析:由题意,AB,CD不共面,故A,B不正确;‎ 经过AC,BD,AD,BC中点的平面与AB,CD平行,故C正确;‎ 若直线AB,CD都与α垂直,可得AB与CD平行,故D不正确.‎ 答案:C ‎115‎ 直线与平面平行的判定与性质 ‎17.(2015河南洛阳二模,文17,直线与平面平行的判定与性质,解答题)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB,现将四边形ABCD沿EF折起,使平面ABEF⊥平面EFDC.‎ ‎(1)若BE=1,是否在折叠后的线段AL上存在一点P,且AP=λPD,使得CP∥平面ABEF?若存在,求出λ的值;若不存在,说明理由.‎ ‎(2)求三棱锥A-CDF的体积的最大值,并求此时点F到平面ACD的距离.‎ 解:(1)存在P,使得CP∥平面ABEF,此时λ=‎3‎‎2‎.‎ 证明:当λ=‎3‎‎2‎,此时APAD‎=‎‎3‎‎5‎,‎ 过P作MP∥FD,与AF交于点M,则MPFD‎=‎‎3‎‎5‎.‎ 又FD=5,∴MP=3.‎ ‎∵EC=3,MP∥FD∥EC,‎ ‎∴MP∥EC,且MP=EC.‎ ‎∴四边形MPCE为平行四边形,∴PC∥ME.‎ ‎∵CP⊄平面ABEF,ME⊂平面ABEF,‎ ‎∴CP∥平面ABEF成立.‎ ‎(2)∵平面ABEF⊥平面EFDC,ABEF∩平面EFDC=EF,AF⊥EF,‎ ‎∴AF⊥平面EFDC.‎ 设BE=x,则AF=x,(0