高中数学选修2-2教学课件复数的三角形式 27页

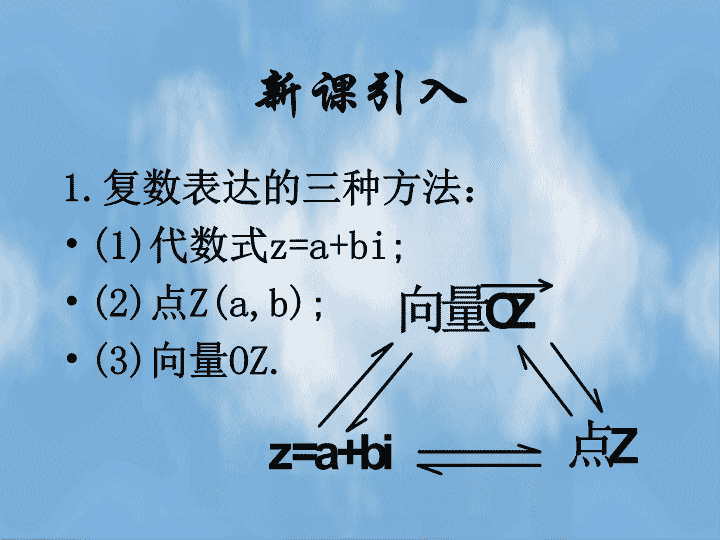
复数的三角形式 仙游一中超越自我 新课引入 1. 复数表达的三种方法： (1) 代数式 z=a+bi; (2) 点 Z(a,b); (3) 向量 OZ. 复习 在复平面上表示出复数 z=a+bi 所对应的点和所对应的向量 OZ. r a b 基本概念 O x y r a b θ 复数的三角形式 r a b θ y x O 复数三角形式的特点： 判断下列复数是不是三角形式 (1)5(sin +icos ) 5[cos( - ) +isin( - )] (2)2(cos -isin ) 2[cos(2π- )+isin(2π- )] (3)2(sin -icos ) 2 （ cos - +isin - ) (4)-3(cos +isin ) 3[cos(π+ )+isin(π+ ) (5)-3(sin +icos ) 3[cos( - )+isin( - )] (6)2(-sin +icos ) 2[cos( + )+isin( + )] (7)2(-cos +isin ) 2[cos(π- )+isin(π- )] 小结： 利用诱导公式转换符号和三角函数名称。 口诀：“奇变偶不变，符号看象限”。 不变名称 变名称 一象限 θ 　　　　 -θ 二象限　　 π-θ 　　　 +θ 三象限　　 π+θ 　　　 +θ 四象限　 2π-θ ， -θ 　　 +θ 练习题 1. 把下列复数表示成三角形式： (1)4 (2)-3 (3)2i (4)-i (5)-2+2i (6)-1-i 2. 把下列复数表示成代数形式： (1)4(cos +isin ) (2)6(cos +isin ) (3) (cos +isin ) (4)3(cos +isin ) (1)4(cos0+isin 0) (2)3(cosπ+isinπ ) (3)2(cos +isin ) (4)cos +isin (5)2 (cos +isin ) (6) (cos +isin ) (1)2+2 i (2)3 +3i (3)-1+i (4)-3i 本节课知识 复数的模和辐角 , 辐角主值的概念 . 复数的模和辐角 , 辐角主值的计算 . r=√a 2 +b 2 ,tg θ=. 复数三角形式和代数形式的转换 . 小结