高中数学选修2-2教学课件第五章 章末复习课 32页

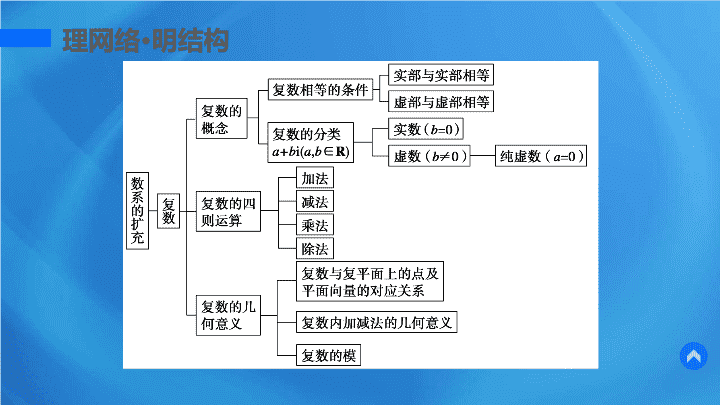
章末复习课 第五章　数系的扩充与复数的引入 内容 索引 01 02 理 网络 明结构 探 题型 提 能力 03 04 理网络 · 明结构 探题型 · 提能力 题型一　分类讨论思想的应用 例 1 　 实数 k 为何值时，复数 (1 ＋ i) k 2 － (3 ＋ 5i) k － 2(2 ＋ 3i) 满足下列条件 ？ (1) 是实数 ； 解　 (1 ＋ i) k 2 － (3 ＋ 5i) k － 2(2 ＋ 3i) ＝ ( k 2 － 3 k － 4) ＋ ( k 2 － 5 k － 6)i. 当 k 2 － 5 k － 6 ＝ 0 ，即 k ＝ 6 或 k ＝－ 1 时，该复数为实数 ． (2) 是虚数 ； 解　 当 k 2 － 5 k － 6 ≠ 0 ， 即 k ≠ 6 且 k ≠ － 1 时，该复数为虚数 ． (3) 是纯虚数． 即 k ＝ 4 时，该复数为纯虚数． 反思与感悟　 当复数的实部与虚部含有字母时，利用复数的有关概念进行分类讨论．分别确定什么情况下是实数、虚数、纯虚数．当 x ＋ y i 没有说明 x ， y ∈ R 时，也要分情况讨论． 跟踪训练 1 　 (1) 若复数 ( a 2 － a － 2) ＋ (| a － 1| － 1)i( a ∈ R ) 不是纯虚数，则 ( 　　 ) A . a ＝－ 1 B . a ≠ － 1 且 a ≠ 2 C . a ≠ － 1 D . a ≠ 2 解析　 若一个复数不是纯虚数 ， 则 该复数是一个虚数或是一个实数 ． 当 a 2 － a － 2 ≠ 0 时，已知的复数一定不是纯虚数 ， 解 得 a ≠ － 1 且 a ≠ 2 ； 当 a 2 － a － 2 ＝ 0 且 | a － 1| － 1 ＝ 0 时 ， 已知 的复数也不是一个纯虚数 ， 解 得 a ＝ 2. 综上所述 ， 当 a ≠ － 1 时 ， 已知 的复数不是一个纯虚数． 答案　 C (2) 实数 x 取什么值时，复数 z ＝ ( x 2 ＋ x － 6) ＋ ( x 2 － 2 x － 15)i 是： ① 实数； ② 虚数； ③ 纯虚数； ④ 零 ． 解　 ① 当 x 2 － 2 x － 15 ＝ 0 ，即 x ＝－ 3 或 x ＝ 5 时，复数 z 为实数； ② 当 x 2 － 2 x － 15 ≠ 0 ，即 x ≠ － 3 且 x ≠ 5 时，复数 z 为虚数； ③ 当 x 2 ＋ x － 6 ＝ 0 且 x 2 － 2 x － 15 ≠ 0 ，即 x ＝ 2 时，复数 z 是纯虚数； ④ 当 x 2 ＋ x － 6 ＝ 0 且 x 2 － 2 x － 15 ＝ 0 ，即 x ＝－ 3 时，复数 z 为零 ． 题型二　数形结合思想的应用 例 2 　 已知等腰梯形 OABC 的顶点 A 、 B 在复平面上对应的复数分别为 1 ＋ 2i ，－ 2 ＋ 6i ， OA ∥ BC . 求顶点 C 所对应的复数 z . 解　 设 z ＝ x ＋ y i ， x ， y ∈ R ，如图． ∵ OA ∥ BC ， | OC | ＝ | BA | ， ∴ k OA ＝ k BC ， | z C | ＝ | z B － z A | ， ∵ | OA | ≠ | BC | ， ∴ x 2 ＝－ 3 ， y 2 ＝ 4( 舍去 ) ，故 z ＝－ 5. 反思与感悟　 数形结合既是一种重要的数学思想，又是一种常用的数学方法．本章中，复数本身的几何意义、复数的模以及复数加减法的几何意义都是数形结合思想的体现且它们得以相互转化．涉及的主要问题有复数在复平面内对应点的位置、复数运算及模的最值问题等． 跟踪训练 2 　已知复数 z 1 ＝ i(1 － i) 3 . (1) 求 | z 1 | ； ( 2) 若 | z | ＝ 1 ，求 | z － z 1 | 的最大值 ． 解　 如图所示， 由 | z | ＝ 1 可知， z 在复平面内对应的点的轨迹是半径为 1 ，圆心为 O (0,0) 的圆， 而 z 1 对应着坐标系中的点 Z 1 (2 ，－ 2) ． 所以 | z － z 1 | 的最大值可以看成是点 Z 1 (2 ，－ 2) 到圆上的点的距离的最大值． 题型三　转化与化归思想的应用 例 3 　 已知 z 是复数， z ＋ 2i ， 均 为实数，且 ( z ＋ a i) 2 的对应点在第一象限，求实数 a 的取值范围． 解　 设 z ＝ x ＋ y i( x ， y ∈ R ) ， 则 z ＋ 2i ＝ x ＋ ( y ＋ 2)i 为实数 ， ∴ y ＝－ 2. ∴ x ＝ 4 . ∴ z ＝ 4 － 2i ， 又 ∵ ( z ＋ a i) 2 ＝ (4 － 2i ＋ a i) 2 ＝ (12 ＋ 4 a － a 2 ) ＋ 8( a － 2)i 在第一象限． ∴ 实数 a 的取值范围是 (2,6) ． 反思与感悟　 在求复数时，常设复数 z ＝ x ＋ y i( x ， y ∈ R ) ，把复数 z 满足的条件转化为实数 x ， y 满足的条件，即复数问题实数化的基本思想在本章中非常重要 ． 跟踪训练 3 　已知 x ， y 为共轭复数，且 ( x ＋ y ) 2 － 3 xy i ＝ 4 － 6i ，求 x ， y . 解　 设 x ＝ a ＋ b i( a ， b ∈ R ) ， 则 y ＝ a － b i. 又 ( x ＋ y ) 2 － 3 xy i ＝ 4 － 6i ， ∴ 4 a 2 － 3( a 2 ＋ b 2 )i ＝ 4 － 6i ， 题型四　类比思想的应用 复数加、减、乘、除运算的实质是实数的加减乘除，加减法是对应实、虚部相加减，而乘法类比多项式乘法，除法类比根式的分子分母有理化，只要注意 i 2 ＝－ 1. 在运算的过程中常用来降幂的公式有 (1)i 的乘方： i 4 k ＝ 1 ， i 4 k ＋ 1 ＝ i ， i 4 k ＋ 2 ＝－ 1 ， i 4 k ＋ 3 ＝－ i( k ∈ Z ) ； (2)(1±i) 2 ＝ ±2i ； 例 4 　 计算： 反思与感悟　 复数的运算可以看作多项式的化简，加减看作多项式加减，合并同类项，乘法和除法可看作多项式的乘法． 呈 重点、现 规律 1. 准确理解虚数单位、复数、虚数、纯虚数、共轭复数、实部、虚部、复数的模等概念． 2. 复数的乘法运算与多项式的乘法运算类似，对于复数的除法运算将分子分母同时乘以分母的共轭复数，最后整理成 a ＋ b i ( a ， b ∈ R ) 的结构形式． 更多精彩内容请 登录 http ://www.91taoke.com 谢谢观看