2019年高考数学高分突破复习课件专题四 第1讲 50页

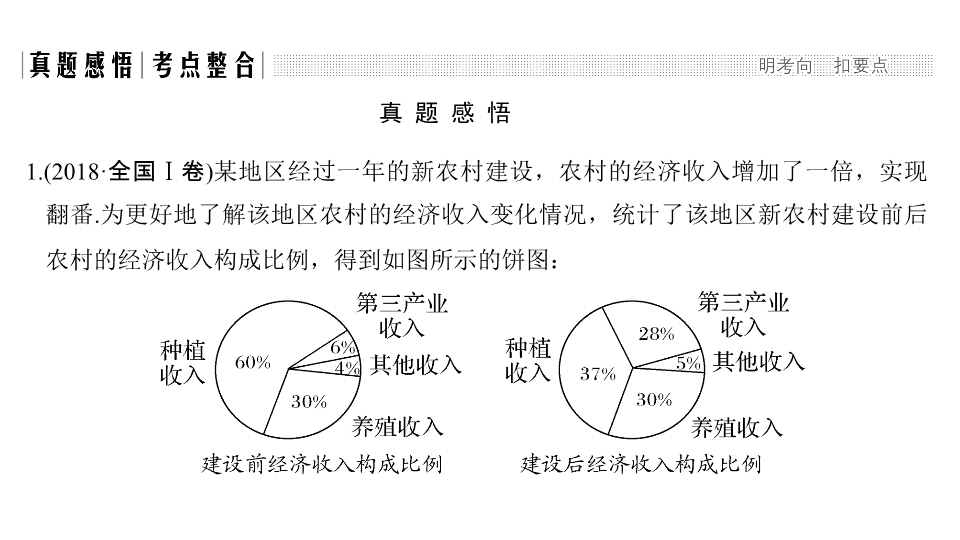
第 1 讲　统计与统计案例 高考定位　 1. 抽样方法、样本的数字特征、统计图表、回归分析与独立性检验主要以选择题、填空题形式命题，难度较小； 2. 注重知识的交汇渗透，统计与概率，回归分析与概率是近年命题的热点， 2016 年， 2017 年和 2018 年在解答题中均有考查 . 1. (2018· 全国 Ⅰ 卷 ) 某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番 . 为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如图所示的饼图： 真 题 感 悟 则下面结论中不正确的是 ( 　　 ) A. 新农村建设后，种植收入减少 B. 新农村建设后，其他收入增加了一倍以上 C. 新农村建设后，养殖收入增加了一倍 D. 新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 解析　 设新农村建设前经济收入为 a ，则新农村建设后经济收入为 2 a ，则由饼图可得新农村建设前种植收入为 0.6 a ，其他收入为 0.04 a ，养殖收入为 0.3 a . 新农村建设后种植收入为 0.74 a ，其他收入为 0.1 a ，养殖收入为 0.6 a ，养殖收入与第三产业收入的总和为 1.16 a ，所以新农村建设后，种植收入减少是错误的 . 故选 A. 答案 　 A 2. (2018· 全国 Ⅲ 卷 ) 某公司有大量客户，且不同年龄段客户对其服务的评价有较大差异 . 为了解客户的评价，该公司准备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样，则最合适的抽样方法是 ________. 解析 　 因为不同年龄段的客户对公司的服务评价有较大差异，所以需按年龄进行分层抽样，才能了解到不同年龄段的客户对公司服务的客观评价 . 答案 　 分层抽样 3. (2018· 全国 Ⅱ 卷 ) 下图是某地区 2000 年至 2016 年环境基础设施投资额 y ( 单位：亿元 ) 的折线图 . (1) 分别利用这两个模型，求该地区 2018 年的环境基础设施投资额的预测值； (2) 你认为用哪个模型得到的预测值更可靠？并说明理由 . (2) 利用模型 ② 得到的预测值更可靠 . 理由如下： 1. 抽样方法 抽样方法包括简单随机抽样、系统抽样、分层抽样，三种抽样方法都是等概率抽样，体现了抽样的公平性，但又各有其特点和适用范围 . 考 点 整 合 2. 统计中的四个数据特征 3. 直方图的两个结论 4. 回归分析与独立性检验   y 1 Y 2 总计 x 1 a b a ＋ b x 2 c d c ＋ d 总计 a ＋ c b ＋ d n 热点一　抽样方法 【例 1 】 (1) (2018· 合肥模拟 ) 某校为了解学生学习的情况，采用分层抽样的方法从高一 1 000 人、高二 1 200 人、高三 n 人中抽取 81 人进行问卷调查，已知高二被抽取的人数为 30 ，那么 n ＝ ( 　　 ) A.860 B.720 C.1 020 D.1 040 (2) (2018· 长沙雅礼中学质检 ) 在一次马拉松比赛中， 35 名运动员的成绩 ( 单位：分钟 ) 的茎叶图如图所示： 若将运动员按成绩由好到差编为 1 ～ 35 号，再用系统抽样方法从中抽取 7 人，则其中成绩在区间 [139 ， 151] 上的运动员人数是 ________. (2) 依题意，可将编号为 1 ～ 35 号的 35 个数据分成 7 组，每组有 5 个数据 . 在区间 [139 ， 151] 上共有 20 个数据，分在 4 个小组内，每组抽取 1 人，共抽取 4 人 . 答案　 (1)D 　 (2)4 【训练 1 】 (1) (2018· 郑州模拟 ) 为规范学校办学，某省教育厅督察组对某所高中进行了抽样调查 . 抽到的班级一共有 52 名学生，现将该班学生随机编号，用系统抽样的方法抽取一个容量为 4 的样本，已知 7 号、 33 号、 46 号同学在样本中，那么样本中还有一位同学的编号应是 ( 　　 ) A.13 B.19 C.20 D.51 ( 2) 某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为 200 ， 400 ， 300 ， 100 件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取 60 件进行检验，则应从丙种型号的产品中抽取 ________ 件 . 解析　 (1) 由系统抽样的原理知，抽样的间隔为 52÷4 ＝ 13 ，故抽取的样本的编号分别为 7 ， 7 ＋ 13 ， 7 ＋ 13 × 2 ， 7 ＋ 13 × 3 ，即 7 号， 20 号， 33 号， 46 号 . ∴ 样本中还有一位同学的编号为 20 号 . 答案　 (1)C 　 (2)18 热点二　用样本估计总体 考法 1 　数字特征与茎叶图的应用 【例 2 － 1 】 (2018· 北京东城区质检 ) 某班男女生各 10 名同学最近一周平均每天的锻炼时间 ( 单位：分钟 ) 用茎叶图记录如下： 假设每名同学最近一周平均每天的锻炼时间是互相独立的 . ① 男生每天锻炼的时间差别小，女生每天锻炼的时间差别大； ② 从平均值分析，男生每天锻炼的时间比女生多； ③ 男生平均每天锻炼时间的标准差大于女生平均每天锻炼时间的标准差； ④ 从 10 个男生中任选一人，平均每天的锻炼时间超过 65 分钟的概率比同样条件下女生锻炼时间超过 65 分钟的概率大 . 其中符合茎叶图所给数据的结论是 ( 　　 ) A. ①②③ B. ②③④ C . ①②④ D . ①③④ 解析　 由茎叶图知，男生每天锻炼时间差别小，女生差别大， ① 正确 . 又根据茎叶图，男生锻炼时间较集中，女生锻炼时间较分散 ， ∴ s 甲 < s 乙 ， ③ 错误， 因此符合茎叶图所给数据的结论是 ①②④ . 答案　 C 考法 2 　用样本的频率分布估计总体分布 【例 2 － 2 】 (2017· 北京卷 ) 某大学艺术专业 400 名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了 100 名学生，记录他们的分数，将数据分成 7 组： [20 ， 30) ， [30 ， 40) ， …[80 ， 90] ，并整理得到如下频率分布直方图： (1) 从总体的 400 名学生中随机抽取一人，估计其分数小于 70 的概率； (2) 已知样本中分数小于 40 的学生有 5 人，试估计总体中分数在区间 [40 ， 50) 内的人数； (3) 已知样本中有一半男生的分数不小于 70 ，且样本中分数不小于 70 的男女生人数相等 . 试估计总体中男生和女生人数的比例 . 解 　 (1) 根据频率分布直方图可知，样本中分数不小于 70 的频率为 (0.02 ＋ 0.04)×10 ＝ 0.6 ， 所以样本中分数小于 70 的频率为 1 － 0.6 ＝ 0.4. 所以从总体的 400 名学生中随机抽取一人，其分数小于 70 的概率估计为 0.4. (2) 根据题意，样本中分数不小于 50 的频率 为 ( 0.01 ＋ 0.02 ＋ 0.04 ＋ 0.02)×10 ＝ 0.9 ， 分数在区间 [40 ， 50) 内的人数为 100 － 100×0.9 － 5 ＝ 5. (3) 由题意可知，样本中分数不小于 70 的学生人数 为 ( 0.02 ＋ 0.04)×10×100 ＝ 60 ， 所以样本中的男生人数为 30×2 ＝ 60 ，女生人数为 100 － 60 ＝ 40 ，男生和女生人数的比例为 60 ∶ 40 ＝ 3 ∶ 2. 所以根据分层抽样原理，总体中男生和女生人数的比例估计为 3 ∶ 2. 探究提高　 1. 平均数与方差都是重要的数字特征，是对数据的一种简明描述，它们所反映的情况有着重要的实际意义 . 平均数、中位数、众数描述数据的集中趋势，方差和标准差描述数据的波动大小 . 2. 在本例 2 － 2 中，抓住频率分布直方图各小长方形的面积之和为 1 ，这是求解的关键；本题易混淆频率分布条形图和频率分布直方图，误把频率分布直方图纵轴的几何意义当成频率，导致样本数据的频率求错 . 答案　 A 【训练 2 】 (1) 如图所示的茎叶图记录了甲乙两组各 5 名工人某日的产量数据 ( 单位：件 ). 若这两组数据的中位数相等，且平均值也相等，则 x 和 y 的值分别为 ( 　　 ) A.3 ， 5 B.5 ， 5 C.3 ， 7 D.5 ， 7 (2) 我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行了调查 . 通过抽样，获得了某年 100 位居民每人的月均用水量 ( 单位：吨 ) ，将数据按照 [0 ， 0.5) ， [0.5 ， 1) ， …… ， [4 ， 4.5] 分成 9 组，制成了如图所示的频率分布直方图 . ① 求直方图中 a 的值； ② 设该市有 30 万居民，估计全市居民中月均用水量不低于 3 吨的人数，说明理由； ③ 估计居民月均用水量的中位数 . 解 　 ① 由频率分布直方图可知：月均用水量在 [0 ， 0.5) 内的频率为 0.08×0.5 ＝ 0.04. 同理，在 [0.5 ， 1) ， [1.5 ， 2) ， [2 ， 2.5) ， [3 ， 3.5) ， [3.5 ， 4) ， [4 ， 4.5] 等组的频率分别为 0.08 ， 0.21 ， 0.25 ， 0.06 ， 0.04 ， 0.02. 由 1 － (0.04 ＋ 0.08 ＋ 0.21 ＋ 0.25 ＋ 0.06 ＋ 0.04 ＋ 0.02) ＝ 0.5× a ＋ 0.5× a ， 解 得 a ＝ 0.30. ② 由 ① 知，该市 100 位居民中月均用水量不低于 3 吨的频率为 0.06 ＋ 0.04 ＋ 0.02 ＝ 0.12 . 由 以上样本的频率分布 ， 可以 估计 30 万居民中月均用水量不低于 3 吨的人数为 300 000×0.12 ＝ 36 000 . ③ 设中位数为 x 吨 . 因为前 5 组的频率之和为 0.04 ＋ 0.08 ＋ 0.15 ＋ 0.21 ＋ 0.25 ＝ 0.73>0.5. 又前 4 组的频率之和为 0.04 ＋ 0.08 ＋ 0.15 ＋ 0.21 ＝ 0.48<0.5. 所以 2 ≤ x <2.5. 由 0.50×( x － 2) ＝ 0.5 － 0.48 ，解得 x ＝ 2.04. 故可估计居民月均用水量的中位数为 2.04 吨 . 热点三　回归分析 【例 3 】 (2018· 成都质检 ) 某省的一个气象站观测点在连续 4 天里记录的 AQI 指数 M 与当天的空气水平可见度 y ( 单位： cm) 的情况如表 1 ： 该省某市 2017 年 11 月份 AQI 指数频数分布如表 2 ： M 900 700 300 100 y 0.5 3.5 6.5 9.5 M [0 ， 200) [200 ， 400) [400 ， 600) [600 ， 800) [800 ， 1 000] 频数 ( 天 ) 3 6 12 6 3 M [0 ， 200) [200 ， 400) [400 ， 600) [600 ， 800) [800 ， 1 000] 日均 收入 ( 元 ) － 2 000 － 1 000 2 000 6 000 8 000 (2) 根据表 3 可知，该月 30 天中有 3 天每天亏损 2 000 元，有 6 天每天亏损 1 000 元，有 12 天每天收入 2 000 元，有 6 天每天收入 6 000 元，有 3 天每天收入 8 000 元 . 【训练 3 】 (2016· 全国 Ⅲ 卷 ) 如图是我国 2008 年至 2014 年生活垃圾无害化处理量 ( 单位：亿吨 ) 的折线图 . 注：年份代码 1 ～ 7 分别对应年份 2008 ～ 2014. (1) 由折线图看出，可用线性回归模型拟合 y 与 t 的关系，请用相关系数加以说明； (2) 建立 y 关于 t 的回归方程 ( 系数精确到 0.01) ，预测 2016 年我国生活垃圾无害化处理量 . 解 　 (1) 由折线图中数据和附注中参考数据得 因为 y 与 t 的相关系数近似为 0.99 ，说明 y 与 t 的线性相关程度相当高，从而可以用线性回归模型拟合 y 与 t 的关系 . 所以预测 2016 年我国生活垃圾无害化处理量将约为 1.82 亿吨 . 热点四　独立性检验 【例 4 】 (2018· 全国 Ⅲ 卷 ) 某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式 . 为比较两种生产方式的效率，选取 40 名工人，将他们随机分成两组，每组 20 人，第一组工人用第一种生产方式，第二组工人用第二种生产方式 . 根据工人完成生产任务的工作时间 ( 单位： min) 绘制了如图所示的茎叶图： (1) 根据茎叶图判断哪种生产方式的效率更高？并说明理由； (2) 求 40 名工人完成生产任务所需时间的中位数 m ，并将完成生产任务所需时间超过 m 和不超过 m 的工人数填入下面的列联表： (3) 根据 (2) 中的列联表，能否有 99% 的把握认为两种生产方式的效率有差异？   超过 m 不超过 m 第一种生产方式     第二种生产方式     ∴ 第二种生产方式的效率更高 . P ( K 2 ≥ k 0 ) 0.050 0.010 0.001 k 0 3.841 6.635 10.828 (2) 由茎叶图数据得到 m ＝ 80. 由此填写列联表如下： (3) 根据 (2) 中的列联表计算 .   超过 m 不超过 m 总计 第一种生产方式 15 5 20 第二种生产方式 5 15 20 总计 20 20 40 所以有 99% 的把握认为两种生产方式的效率有差异 . 【训练 4 】 微信是腾讯公司推出的一种手机通讯软件，它支持发送语音短信、视频、图片和文字，一经推出便风靡全国，甚至涌现出一批在微信的朋友圈内销售商品的人 ( 被称为微商 ). 为了调查每天微信用户使用微信的时间，某经销化妆品的微商在一广场随机采访男性、女性用户各 50 名，将男性、女性使用微信的时间分成 5 组： (0 ， 2] ， (2 ， 4] ， (4 ， 6] ， (6 ， 8] ， (8 ， 10] 分别加以统计，得到如图所示的频率分布直方图 . (1) 根据女性频率分布直方图估计女性使用微信的平均时间； (2) 若每天玩微信超过 4 小时的用户列为 “ 微信控 ” ，否则称其为 “ 非微信控 ” ，请你根据已知条件完成 2×2 的列联表，并判断是否有 90% 的把握认为 “ 微信控 ” 与 “ 性别有关 ” ？ 解 　 (1) 女性平均使用微信的时间为： 0.16×1 ＋ 0.24×3 ＋ 0.28×5 ＋ 0.2×7 ＋ 0.12×9 ＝ 4.76( 小时 ). (2) 由已知得： 2(0.04 ＋ a ＋ 0.14 ＋ 2×0.12) ＝ 1 ，解得 a ＝ 0.08. 由题设条件得列联表 所以有 90% 的把握认为 “ 微信控 ” 与 “ 性别 ” 有关 .   微信控 非微信控 总计 男性 38 12 50 女性 30 20 50 总计 68 32 100 1. 用样本估计总体是统计的基本思想 . 用 样本频率分布来估计总体分布的重点是频率分布表和频率分布直方图的绘制及用样本频率分布估计总体分布；难点是频率分布表和频率分布直方图的理解及应用 . 2.(1) 众数、中位数及平均数都是描述一组数据集中趋势的量，平均数是最重要的量，与每个样本数据有关，这是中位数、众数所不具有的性质 . ( 2) 标准差、方差描述了一组数据围绕平均数波动的大小 . 标准差、方差越大，数据的离散程度就越大 . 3. 茎叶图、频率分布表和频率分布直方图 4. 回归分析是对具有相关关系的两个变量进行统计分析的方法，只有在散点图大致呈线性时，求出的线性回归方程才有实际意义，否则，求出的线性回归方程毫无意义 . 根据回归方程进行预报，仅是一个预报值，而不是真实发生的值 .