高中数学选修2-3教学课件：回归分析的基本思想及其初步应用(1) 23页

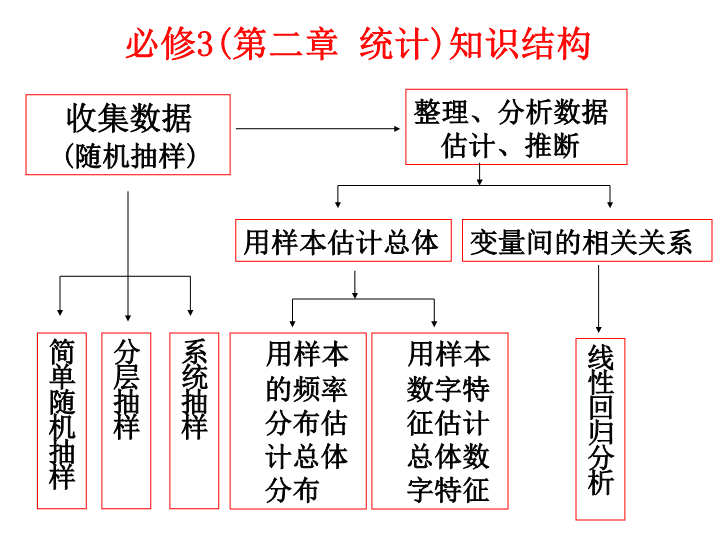
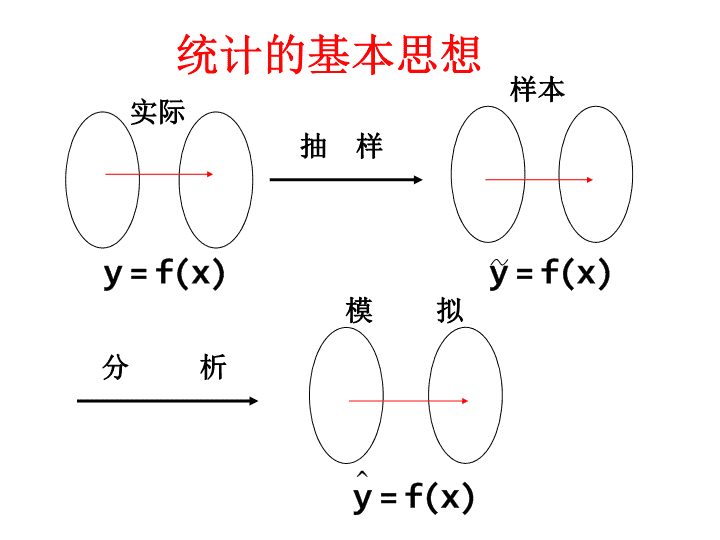
3.1 回归分析的基本思想及初步应用 (1) 必修 3( 第二章 统计 ) 知识结构 收集数据 ( 随机抽样 ) 整理、分析数据估计、推断 简单随机抽样 分层抽样 系统抽样 用样本估计总体 变量间的相关关系 用样本的频率分布估计总体分布 用样本数字特征估计总体数字特征 线性回归分析 统计的基本思想 实际 样本 模 拟 抽 样 分 析 问题 1 ： 正方形的面积 y 与正方形的边长 x 之间 的 函数关系 是 y = x 2 确定性关系 问题 2 ： 某水田水稻产量 y 与施肥量 x 之间是否 ------- 有一个确定性的关系？ 例如： 在 7 块并排、形状大小相同的试验田上 进行施肥量对水稻产量影响的试验，得到如下所示的一组数据： 施化肥量 x 15 20 25 30 35 40 45 水稻产量 y 330 345 365 405 445 450 455 复习、变量之间的两种关系 自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做 相关关系 。 1 、定义： 1 ）：相关关系是一种不确定性关系； 注 对具有相关关系的两个变量进行统计分析的方法叫 回归分析 。 2 ）： 2 、 现实生活中存在着大量的相关关系。 如：人的身高与年龄； 产品的成本与生产数量； 商品的销售额与广告费； 家庭的支出与收入。等等 探索：水稻产量 y 与施肥量 x 之间大致有何规律？ 10 20 30 40 50 500 450 400 350 300 · · · · · · · 发现：图中各点，大致分布在某条直线附近。 探索 2 ：在这些点附近可画直线不止一条， 哪条直线最能代表 x 与 y 之间的关系呢？ x y 施化肥量 水稻产量 施化肥量 x 15 20 25 30 35 40 45 水稻产量 y 330 345 365 405 445 450 455 散点图 10 20 30 40 50 500 450 400 350 300 · · · · · · · x y 施化肥量 水稻产量 最小二乘法： 称为样本点的中心 。 3 、对两个变量进行的线性分析叫做 线性回归分析 。 2 、回归直线方程： 2. 相应的直线叫做 回归直线 。 1 、所求直线方程 叫做 回归直 --- 线方程 ；其中 相关系数 1. 计算公式 2 ．相关系数的性质 (1)|r|≤1 ． (2)|r| 越接近于 1 ，相关程度越大； |r| 越接近于 0 ，相关程度越小． 问题：达到怎样程度， x 、 y 线性相关呢？它们的相关程度怎样呢？ 负相关 正相关 相关系数 ｒ＞０正相关；ｒ＜０负相关．通常， r ∈ [- 1 ,- 0.75]-- 负相关很强 ; r ∈ [0.75,1]— 正相关很强 ; r ∈ [-0.75,-0.3]-- 负相关一般 ; r ∈ [0.3, 0.75]— 正相关一般 ; r ∈ [- 0.25 , 0.25]-- 相关性较弱 ; · · · · · · · 10 20 30 40 50 500 450 400 350 300 x y 施化肥量 水稻产量 施化肥量 x 15 20 25 30 35 40 45 水稻产量 y 330 345 365 405 445 450 455 解 : 1. 画出散点图 2. 求出 3. 写出回归方程 4. 计算相关系数 例题 1 从某大学中随机选出 8 名女大学生，其身高和体重数据如下表： 编号 1 2 3 4 5 6 7 8 身高 165 165 157 170 175 165 155 170 体重 48 57 50 54 64 61 43 59 求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为 172 ｃｍ的女大学生的体重。　 分析：由于问题中要求根据身高预报体重，因此选取身高为自变量，体重为因变量． 3. 通过探究栏目引入“线性回归模型”。此处可以引导学生们体会函数模型与回归模型之间的差别。 （ 2 ）从散点图还可以看到，样本点散布在某一条直线的附近，而不是一条直线上，所以不能用一次函数ｙ＝ｂｘ＋ａ来描述它们之间的关系。这时我们用下面的线性回归模型来描述身高和体重的关系：ｙ＝ｂｘ＋ａ + ｅ其中ａ和ｂ为模型的 未知参数 ， e 是 y 与 之间的误差 , 通常 ｅ称为 随机误差 。 （ 1 ）由图形观察可以看出，样本点呈条状分布，身高和体重有比较好的线性相关关系，因此可以用线性回归方程刻画它们之间的关系。 线性回归模型 ｙ＝ｂｘ＋ａ + ｅ ｙ＝ｂｘ＋ａ + ｅ其中ａ和ｂ为模型的 未知参数 ， e 是 y 与 之间的误差 , 通常 ｅ称为 随机误差 。 为了衡量预报的精度 , 需要估计的 σ 2 值 ? （ 1 ）根据散点图来粗略判断它们是否线性相关。 （ 2 ）是否可以用线性回归模型来拟合数据 （ 3 ）通过残差 来判断模型拟合的效 果这种分析工作称为 残差分析 使学生了解残差图的制作及作用。 P98 坐标纵轴为残差变量，横轴可以有不同的选择； 若模型选择的正确， 残差图中的点应该分布在以横轴为心的带形区域； 对于远离横轴的点，要特别注意 。 错误数据 模型问题 身高与体重残差图 异常点 作业：Ｐ １０４ 习题３．１　第１题