- 1.06 MB
- 2021-06-24 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
数学(文)
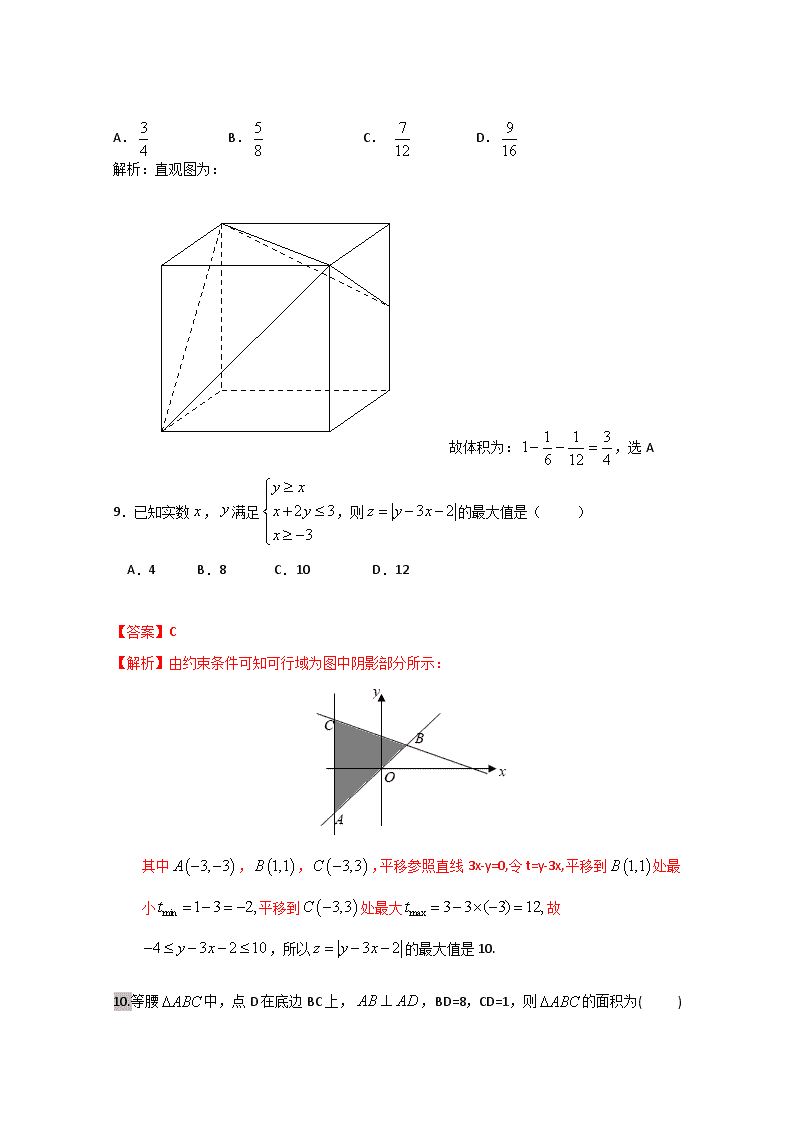
一. 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设集合,则( )
A. B. C. D.
答案B
2. 已知复数(为虚数单位),则复数的虚部是( )。
A.1 B.-1 C. D.
【答案】B
【解析】∵,∴复数的虚部是,
故选:B.
3.设,,,则( )
A. B. C. D.
答案D
4.已知命题p:;命题q:若,则a0.75,说明y与x的线性相关程度相当高,从而可以用线性回归模型拟合y与x的关系.
(2)∴=0.7,=1.05,∴=0.7x+1.05.
将x=6代入回归直线方程,
得=0.7×6+1.05=5.25(小时).
∴预测包装10个商品包装需要5.25小时.
(3)由题意可得
当掌握知识点个数x=3时,学生的学习功效值z取最大值9.
20. 已知抛物线的顶点在原点,焦点在坐标轴上,点为抛物线上一点.
(1)求的方程;
(2)若点在上,过作的两弦与,若,求证:直线过定点.
【答案】(1)或; (2)证明见解析.
【解析】
(1)当焦点在轴时,设的方程为,代人点得,即.
当焦点在轴时,设的方程为,代人点得,即,
综上可知:的方程为或. ············4分
(2)因为点在上,所以曲线的方程为. ········5分
设点,
直线,显然存在,联立方程有:.··········7分,
即即.··········9分
直线即············11分
直线过定点. ············12分
21. 已知函数
(1)求函数在区间的最小值;
(2)若函数在上有两个零点且﹐证明:
【解】(1)由,令,则
在上单调递增,又
所以存在,使得,所以在上,单调递减,
在上,单调递增,又,所以对
恒成立,即,所以函数在区间单调递减,
(2)证明:由(1)知函数在区间单调递减,
时,单调递增,又
所以时,,所以函数在区间单调递增,
函数在上有两个零点即与的图像有两个交点,则,且. 要证只需证,又
只需证,又,只需证,即证.
设即
,所以在单调递增,
所以,所以成立,故
(二)选作题(10分):请考生在第22、23题中任选一题做答.多答按所答的首题进行评分.
22.在平面直角坐标系中,直线的普通方程是,曲线
的参数方程是,在以为极点,轴正半轴为极轴建立极坐标系中,曲线的极坐标方程是.
(1) 写出及的极坐标方程;
(2) 已知,与交于两点,与交于两点,求的最大值.
解:(1)直线的极坐标方程是;
曲线的极坐标方程是
(2):,
23.(1)已知函数,解不等式
(2)已知均为正数,求证:
解:(1)当时,原不等式化为
当时,原不等式化为
当时,原不等式化为
综上所知:原不等式的解集为
(2)证明:
,当且仅当时等号成立
以上三个式子相加可得: