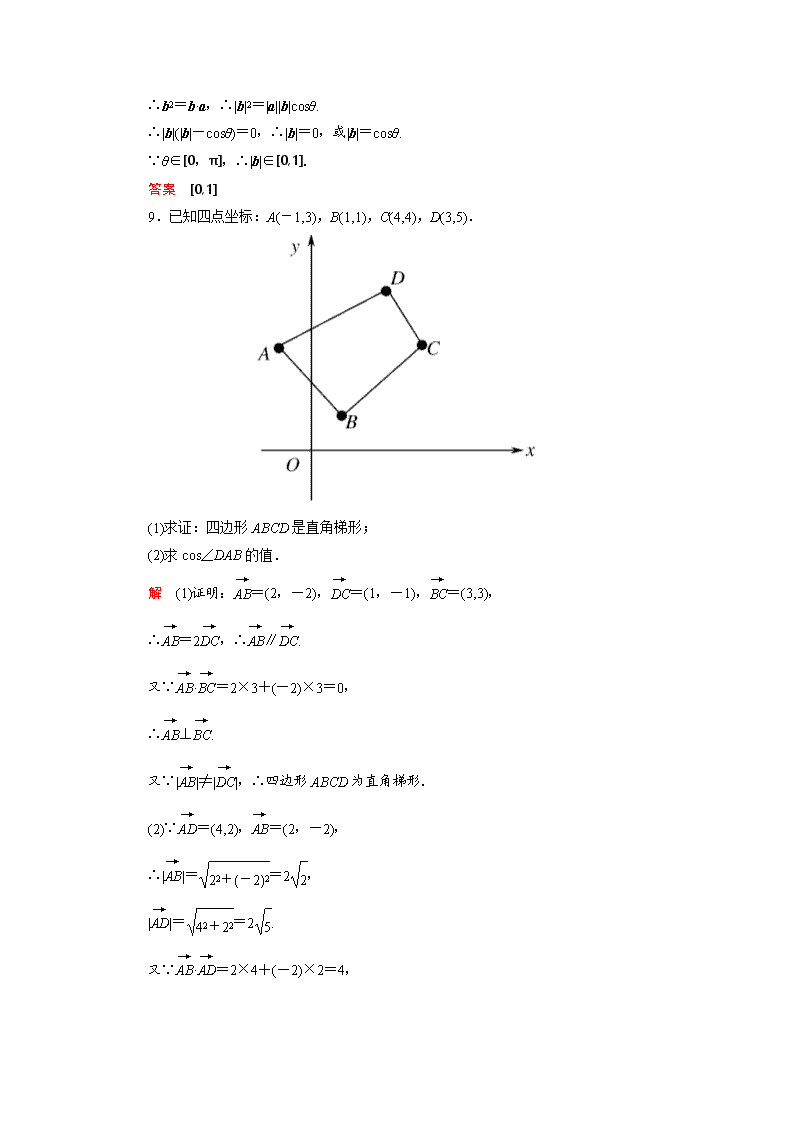高中数学（人教A版）必修4：2-4-2同步试题（含详解） 5页

高中数学(人教A版)必修4同步试题 ‎1．若a＝(3,4)，b＝(5,12)，则a与b夹角的余弦值为(　　)‎ A.　　　　　　　　 B. C．－ D．－ 解析　设a与b的夹角为θ，依题意cosθ＝＝＝.‎ 答案　A ‎2．已知向量a＝(－2,1)，b＝(1，y)，a⊥b，则y等于(　　)‎ A．－1 B．1‎ C．－2 D．2‎ 答案　D ‎3．已知A，B，C是坐标平面上的三点，其坐标分别为A(1,2)，B(4,1)，C(0，－1)，则△ABC的形状为(　　)‎ A．直角三角形 B．等腰三角形 C．等腰直角三角形 D．以上均不正确 解析　＝(3，－1)，＝(－1，－3)，＝(－4，－2)，∴||＝，||＝，||＝.‎ ‎∴||＝||，且||2＋||2＝||2＝20.‎ ‎∴△ABC为等腰直角三角形，应选C.‎ 答案　C ‎4．已知a＝(0,1)，b＝(3，x)，向量a与b的夹角为，则x的值为(　　)‎ A．±3 B．± C．±9 D．3‎ 解析　cos＝＝，‎ ‎∴2x＝，且x>0，∴3x2＝27，∴x＝3.‎ 答案　D ‎5．已知向量a＝(1,2)，b＝(2，－3)，若向量c满足(c＋a)∥b，c⊥(a＋b)，则c＝(　　)‎ A. B. C. D. 解析　不妨设c＝(m，n)，则a＋c＝(1＋m,2＋n)，a＋b＝(3，－1)，‎ 对于(c＋a)∥b，则有－3(1＋m)＝2(2＋n)．‎ 又c⊥(a＋b)，则有‎3m－n＝0，‎ ‎∴m＝－，n＝－.‎ 答案　D ‎6．已知向量a＝(1，－2)，b＝(2，λ)，且a与b夹角为锐角，则实数λ的取值范围是________．‎ 解析　a·b＝2－2λ，|a|＝，|b|＝，由a与b的夹角为锐角，得＝>0，即2－2λ>0，∴λ<1.‎ 当＝1时，解得λ＝－4，此时a与b夹角为0°，不合题意．‎ ‎∴λ≠－4.故λ的取值范围是(－∞，－4)∪(－4,1)．‎ 答案　(－∞，－4)∪(－4,1)‎ ‎7．已知向量a＝(x，y)，b＝(－1,2)，且a＋b＝(1,3)，则|a－2b|等于________．‎ 解析　a＋b＝(x－1，y＋2)＝(1,3)，‎ ‎∴x＝2，y＝1，∴a＝(2,1)．‎ 又|a|＝，|b|＝，a·b＝0，‎ ‎∴|a－2b|2＝|a|2－‎4a·b＋4|b|2＝25.‎ ‎∴|a－2b|＝5.‎ 答案　5‎ ‎8．已知a是平面内的单位向量，若向量b满足b·(a－b)＝0，则|b|的取值范围是________．(用数字作答)‎ 解析　由题意知|a|＝1，设a与b的夹角为θ，则 b·(a－b)＝b·a－b2＝0，‎ ‎∴b2＝b·a，∴|b|2＝|a||b|cosθ.‎ ‎∴|b|(|b|－cosθ)＝0，∴|b|＝0，或|b|＝cosθ.‎ ‎∵θ∈[0，π]，∴|b|∈[0,1]．‎ 答案　[0,1]‎ ‎9．已知四点坐标：A(－1,3)，B(1,1)，C(4,4)，D(3,5)．‎ ‎(1)求证：四边形ABCD是直角梯形；‎ ‎(2)求cos∠DAB的值．‎ 解　(1)证明：＝(2，－2)，＝(1，－1)，＝(3,3)，‎ ‎∴＝2，∴∥.‎ 又∵·＝2×3＋(－2)×3＝0，‎ ‎∴⊥.‎ 又∵||≠||，∴四边形ABCD为直角梯形．‎ ‎(2)∵＝(4,2)，＝(2，－2)，‎ ‎∴||＝＝2，‎ ‎||＝＝2.‎ 又∵·＝2×4＋(－2)×2＝4，‎ ‎∴cos∠DAB＝＝＝.‎ ‎10．在平面直角坐标系xOy中，已知点A(－1，－2)，B(2,3)，C(－2，－1)．‎ ‎(1)求以线段AB，AC为邻边的平行四边形两条对角线的长；‎ ‎(2)设实数t满足(－t)·＝0，求t的值．‎ 解　(1)由题设知＝(3,5)，＝(－1,1)，‎ 则＋＝(2,6)，－＝(4,4)．‎ ‎∴|＋|＝2，|－|＝4.‎ 故所求的两条对角线长分别为4，2.‎ ‎(2)由题设知＝(－2，－1)，－t＝(3＋2t,5＋t)．‎ 由(－t)·＝0，‎ 得(3＋2t,5＋t)·(－2，－1)＝0，从而5t＝－11，‎ ‎∴t＝－.‎ 教师备课资源 ‎1.已知a＝(2，－3)，b＝(1，－2)，且c⊥a，b·c＝1，则c的坐标为(　　)‎ A．(3，－2) B．(3,2)‎ C．(－3，－2) D．(－3,2)‎ 解析　采用验证的方法知，c＝(－3，－2)满足c·a＝－6＋6＝0，所以c⊥a，b·c＝1×(－3)＋(－2)×(－2)＝1.因此可选C.‎ 答案　C ‎2．下列4个说法：‎ ‎①共线的单位向量是相等向量；‎ ‎②若a，b，c满足a＋b＝c时，则以|a|，|b|，|c|为边一定能构成三角形．‎ ‎③对任意的向量，必有|a＋b|≤|a|＋|b|.‎ ‎④(a＋b)·c＝a·c＋b·c.‎ 把你认为正确的序号填在横线上__________．‎ 解析　①中共线的单位向量当方向相反时，不成立．②中当a＋b与c共线时，不成立．③正确，由向量的几何意义可知．④正确．应填③④.‎ 答案　③④‎ ‎3．若向量a≠0，b＝，c＝(cosθ，sinθ)，则(b＋c)·(b－c)＝________.‎ 解析　(b＋c)·(b－c)＝b2－c2‎ ‎＝|b|2－|c|2＝1－1＝0.‎ 答案　0‎ ‎4．已知a＝(1,0)，b＝(1,1)，当λ为何值时，a＋λb与a垂直？‎ 解　∵a＝(1,0)，b＝(1,1)，‎ ‎∴a＋λb＝(1,0)＋λ(1,1)＝(1＋λ，λ)．‎ 由于a＋λb与a垂直，‎ ‎∴1＋λ＋0＝0，∴λ＝－1.‎ ‎∴当λ＝－1时，a＋λb与a垂直．‎ ‎5．已知a＝(2,3)，b＝(－4,7)，则a在b上的射影的数量为(　　)‎ A. B. C. D. 解析　∵a＝(2,3)，b＝(－4,7)，∴a·b＝2×(－4)＋3×7＝13，|a|＝，|b|＝，‎ ‎∴cosθ＝＝.‎ ‎∴a在b上的射影为 ‎|a|cosθ＝×＝.‎ 答案　C