2021届课标版高考理科数学大一轮复习课件：2-4　指数与指数函数（讲解部分） 12页

考点一    指数及指数幂的运算 考点清单 考向基础 1.根式的概念 根式的概念 符号表示 备注 一般地,如果 x n = a ,那么 x 叫做 a 的 n 次方根 — n >1且 n ∈N * 当 n 是奇数时,正数的 n 次方根是一个正数,负数的 n 次方根是一个负数   零的 n 次方根是零 当 n 是偶数时,正数的 n 次方根有两个,这两个数互为相反数 ±   ( a >0) 负数没有偶次方根 2.两个重要公式   =   (   ) n = a (注意 a 必须使   有意义). 3.有理指数幂 (1)幂的有关概念 (i)正分数指数幂:   =   ( a >0, m , n ∈N * ,且 n >1); (ii)负分数指数幂:   =   =   ( a >0, m , n ∈N * ,且 n >1); (iii)0的正分数指数幂等于0,0的负分数指数幂没有意义. (2)有理指数幂的性质 (i) a r a s = a r + s ( a >0, r , s ∈Q); (ii)( a r ) s = a rs ( a >0, r , s ∈Q); (iii)( ab ) r = a r b r ( a >0, b >0, r ∈Q). 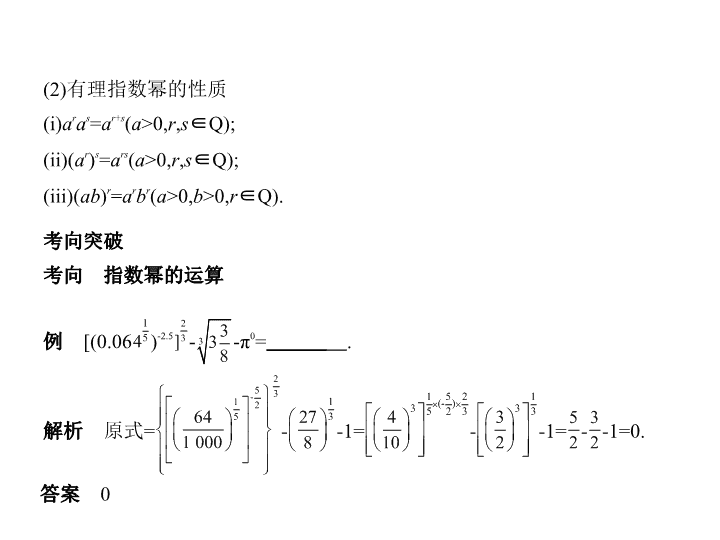考向突破 考向    指数幂的运算 例　 [(0.06   ) -2.5   -   -π 0 = 　　　     . 解析 　原式=   -   -1=   -   -1=   -   -1=0. 答案 　0 考点二    指数函数的图象与性质 考向基础 1.指数函数的图象与性质 a >1 0< a <1 图象     定义域 R 值域 (0,+ ∞ ) 性质 过定点 (0,1) 当 x >0时, y >1;当 x <0时,0< y <1 当 x >0时,0< y <1;当 x <0时, y >1 在(- ∞ ,+ ∞ )上是 单调增函数 在(- ∞ ,+ ∞ )上是 单调减函数 2.指数函数在同一直角坐标系中的图象的相对位置与底数大小的关系如 图所示,其中0< c < d <1< a < b .   在 y 轴右侧,图象从上到下相应的底数由大变小; 在 y 轴左侧,图象从下到上相应的底数由大变小. (无论在 y 轴的左侧还是右侧,底数按逆时针方向变大) 考向突破 考向一    指数式大小比较 例1     (2019安徽合肥4月冲刺,2)若0< b < a <1,则在 a b , b a , a a , b b 中最大的是   (    　) A. b a 　　　　    B. a a 　　　　    C. a b 　　　　    D. b b 解析 　∵0< b < a <1,∴指数函数 y = a x 和 y = b x 均为减函数, ∴ a b > a a , b a < b b ,∵幂函数 y = x b 在(0,+ ∞ )上为增函数, ∴ a b > b b ,即在 a b , b a , a a , b b 中最大的是 a b ,故选C. 答案     C 考向二    指数函数的图象与性质及其应用 例2 　已知函数 f ( x )=|2 x -1|, a < b < c ,且 f ( a )> f ( c )> f ( b ),则下列结论中,一定成立的 是       (　　) A. a <0, b <0, c <0 　　　　    B. a <0, b ≥ 0, c >0 C.2 - a <2 c 　　　　    D.2 a +2 c <2 解析 　作出函数 f ( x )=|2 x -1|的图象(如图中实线所示),由 a < b < c ,且 f ( a )> f ( c )> f ( b ),结合图象知 f ( a )<1, a <0, f ( c )<1,0< c <1,∴0<2 a <1,1<2 c <2,   ∴ f ( a )=|2 a -1|=1-2 a , f ( c )=|2 c -1|=2 c -1. 又 f ( a )> f ( c ),即1-2 a >2 c -1, ∴2 a +2 c <2,故选D. 答案     D 方法      与指数函数有关的复合函数的解题方法 1.与指数函数有关的复合函数的定义域、值域 (1) y = a f ( x ) 的定义域就是 f ( x )的定义域. (2) y = a f ( x ) 和 y = f ( a x )的值域的解法 ①形如 y = a f ( x ) 的函数的值域,要先令 u = f ( x ),求出 u = f ( x )的值域,再结合 y = a u 的 单调性求出 y = a f ( x ) 的值域.若 a 的取值范围不确定,则需要对 a 进行分类讨论: 当0< a <1时, y = a u 为减函数;当 a >1时, y = a u 为增函数. ②形如 y = f ( a x )的函数的值域,要先求出 u = a x 的值域,再结合 y = f ( u )的单调性确 定 y = f ( a x )的值域. 方法技巧 2.与指数函数有关的复合函数的单调性 形如 y = a f ( x ) 的函数的单调性,它的单调区间与 f ( x )的单调区间有关: 若 a >1,函数 f ( x )的单调增(减)区间即函数 y = a f ( x ) 的单调增(减)区间;若0< a <1, 函数 f ( x )的单调增(减)区间即函数 y = a f ( x ) 的单调减(增)区间.即“同增异减”. 注意　当底数 a 与1的大小不确定时应分类讨论. 3.对于含有 a x , a 2 x 的函数表达式,通常可以令 t = a x 进行换元,但换元过程中要 注意新元的取值范围. 例 　已知 f ( x )是定义在R上的单调函数且 f ( x )为奇函数,满足 f (3)=log 2 3,若 f ( k · 3 x )+ f (3 x -9 x -2)<0对任意 x ∈R恒成立,则 k 的取值范围是 　　　　　     . 解析 　由题意知 f (0)=0,又 f (3)=log 2 3>0,所以 f (3)> f (0),因为 f ( x )是R上的单调 函数,所以 f ( x )在R上是增函数. f ( k ·3 x )+ f (3 x -9 x -2)<0 ⇔ f ( k ·3 x )< f (9 x -3 x +2) ⇔ k ·3 x <9 x -3 x +2,即(3 x ) 2 -(1+ k )3 x +2>0对任 意 x ∈R恒成立. 解法一:(换元法)令 t =3 x , t >0,问题等价于 t 2 -(1+ k ) t +2>0对任意 t >0恒成立. 令 g ( t )= t 2 -(1+ k ) t +2,其对称轴为 t =   , 当 t =   ≤ 0,即 k ≤ -1时, g (0)=2>0,符合题意; 当 t =   >0,即 k >-1时,需满足 g   >0,解得-1< k <-1+2   . 综上所述,当 k <-1+2   时, f ( k ·3 x )+ f (3 x -9 x -2)<0对任意 x ∈R恒成立. 解法二:(分离参数法)分离参数 k 得 k <3 x +   -1,令 u =3 x +   -1,则 u ≥ 2   -1   ,即 u 的最小值为2   -1,故要使不等式 k <3 x +   -1 对任意 x ∈R恒成立,只要 k <2   -1即可. 答案      k <2   -1