2015届高考数学二轮复习专题训练试题：函数的应用（2） 14页

‎ 函数的应用（2）‎ ‎1、周期为4的函数 其中m>0，若方程‎3f（x）=x恰有5个实数解，则m的取值范围为                                         （    ）A．           B．               C．            D．‎ ‎2、设函数，表示不超过的最大整数，如 则函数的值域为（     ）A .      B .      C .     D . ‎ ‎3、对于函数在使成立的所有常数中，我们把的最大值叫做的下确界，则对于正数，的下确界A．             B．            C．              D．‎ ‎4、已知点在直线上运动，则的最小值是      A．       B．2         C．2                  D．4‎ ‎5、 函数与有相同的定义域，且都不是常值函数，对于定义域内的任何, 有,,且当时，，则的奇偶性为 Ａ．奇函数非偶函数　Ｂ．偶函数非奇函数　Ｃ．既是奇函数又是偶函数　Ｄ．非奇非偶函数 ‎6、设，又记则（     ）              ‎ A                B              C             D  ‎ ‎7、已知：a1＜a2＜a3，b1＜b2＜b3，a1＋a2＋a3＝b1＋b2＋b3，a‎1a2＋a‎1a3＋a‎2a3＝b1b2＋b1b3 +b2b3且a1＜b1，有下列四个命题（1）b2＜a2；      （2）a3＜b3；         （3）a‎1a2a3＜b1b2b3；（‎ ‎      （4）(1－a1)(1－a2)(1－a3)＞(1－b1)(1－b2)(1－b3)，其中真命题个数为 ‎      A．1                         B．2                        C．3                        D．4‎ ‎9、设是定义在R上的恒不为零的函数，且对任意的实数，都有，若，则数列的前n项和的取值范围为                                （    ）‎ ‎       A．                B．                C．                 D．‎ ‎10、．若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为一同族函数．函数的解析式为，值域为的同族函数共有 ‎  7个         8个           9个         10个 ‎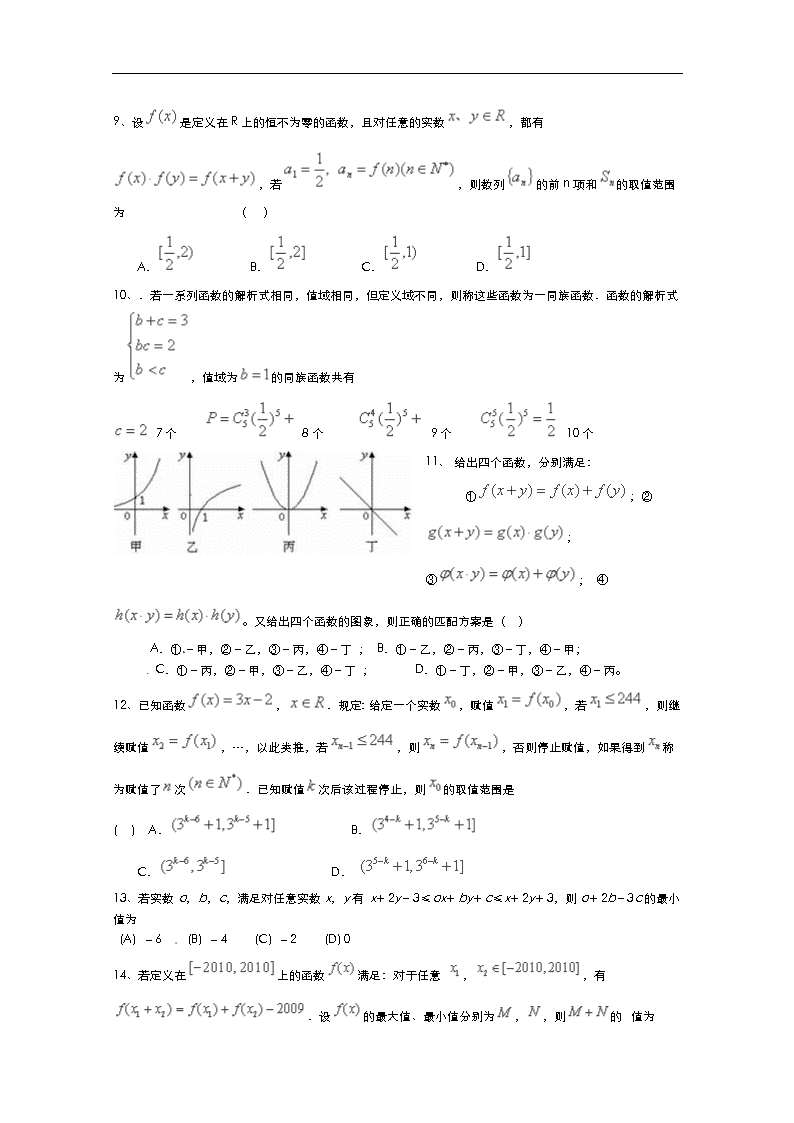11、 给出四个函数，分别满足：‎ ‎           ①；②；‎ ‎③； ④。又给出四个函数的图象，则正确的匹配方案是（　）‎ ‎           A．①－甲，②－乙，③－丙，④－丁 ； B．①－乙，②－丙，③－丁，④－甲；‎ ‎           C．①－丙，②－甲，③－乙，④－丁 ；            D．①－丁，②－甲，③－乙，④－丙。‎ ‎12、已知函数，．规定：给定一个实数，赋值，若，则继续赋值，…，以此类推，若，则，否则停止赋值，如果得到称为赋值了次．已知赋值次后该过程停止，则的取值范围是(    )    A．                      B．‎ ‎       C．                               D．       ‎ ‎13、若实数a，b，c，满足对任意实数x，y有 x＋2y－3≤ax＋by＋c≤x＋2y＋3，则a＋2b－‎3c的最小值为 ‎ (A) －6       (B) －4        (C) －2        (D) 0‎ ‎14、若定义在上的函数满足：对于任意 ，，有．设的最大值、最小值分别为，，则的  值为 A．2009           B．2010           C．4018           D．4020‎ ‎15、 函数，其中，若动直线与函数的图像有三个不同的交点，它们的横坐标分别为，则是否存在最大值？若存在，在横线处填写其最大值；若不存在，直接填写“不存在”______________.‎ ‎16、对于函数，，对于区间上的任意实数，有如下条件： ，其中能使恒成立的条件的序号有_________。（写出你认为成立的所有条件序号）‎ ‎17、已知二次函数的值域为，则的最小值为       .‎ ‎18、已知函数是定义在上的奇函数，当时，给出以下命题：‎ ‎①当时，；        ②函数有五个零点；[来源:Z*xx*k.Com]‎ ‎③若关于的方程有解，则实数的取值范围是；④对恒成立．‎ 其中，正确命题的序号是                     ． ‎ ‎19、若二次函数的图象和直线y=x无交点，现有下列结论：‎ ‎    ①方程一定没有实数根；    ②若a>0，则不等式对一切实数x都成立；‎ ‎    ③若a<0，则必存在实数，使; ④函数的图象与直线y=-x一定没有交点，‎ ‎    其中正确的结论是____________（写出所有正确结论的编号）．‎ ‎20、已知表示不超过的最大整数，如：．‎ 定义．给出如下命题：① 使成立的的取值范围是；‎ ‎② 函数的定义域为，值域为；③ 1006；‎ ‎④ 设函数，则函数的不同零点有3个．‎ 其中正确的命题的序号是                     ．‎ ‎21、给出定义:若 (其中为整数),则叫做与实数“亲密的整数”, ‎ 记作,在此基础上给出下列关于函数的四个命题:①函数在 上是增函数;②函数的图象关于直线对称;③函数 是周期函数,最小正周期为1;④当时，函数有两个零点. 其中 正确命题的序号是____________.(A)  ②③④      (B) ①③       (C)  ①②       (D)  ②④‎ ‎22、下列说法正确的有________：‎ ‎①对于函数f(x)＝x2＋mx＋n，若f(a)＞0， f(b)＞0，则函数f(x)在区间(a，b)内一定没有零点．‎ ‎②函数f(x)＝2x－x2有两个零点．③若奇函数、偶函数有零点，其和为0.④当a＝1时，函数f(x)＝|x2－2x|－a有三个零点．‎ ‎23、四位同学在研究函数时，分别给出下面四个结论：①函数的图象关于轴对称；② 函数的值域为 (－1,1)；③若则一定有；④若规定, ，则 对任意恒成立．你认为上述四个结论中正确的有       ‎ ‎24、已知函数，对于下列命题：‎ ‎    ①函数的最小值是0；   ②函数在上是单调递减函数；   ③若；‎ ‎    ④若函数有三个零点，则的取值范围是； ⑤函数关于直线对称．‎ ‎       其中正确命题的序号是___▲___．（填上你认为所有正确命题的序号）．‎ ‎25、设二次函数的值域为，则的最大值为   ‎ ‎26、函数的图象形如汉字“囧”，故称其为“囧函数”.下列命题正确的是             .‎ ‎①“囧函数”的值域为；                ②“囧函数”在上单调递增；‎ ‎③“囧函数”的图象关于轴对称；        ④“囧函数”有两个零点；‎ ‎⑤“囧函数”的图象与直线的图象至少有一个交点.‎ ‎27、对任意实数，函数，如果函数，那么函数的最大值等于            ． ‎ ‎28、若函数的零点有且只有一个，则实数___________. ‎ ‎29、 将函数的图像绕坐标原点逆时针方向旋转角，得到曲线.若对于每一个旋转角，曲线都是一个函数的图像，则的最大值为__________ ‎ ‎30、设函数的定义域为D，若存在非零实数，使得对于都有且，则称为M上的高调函数. 现给出下列命题：①函数为R上的1高调函数；‎ ‎②函数为R上的高调函数；‎ ‎③若定义域为的函数是上的高调函数，则实数的取值范围是. ‎ 其中正确的命题是          .（写出所有正确命题的序号） ‎ ‎31、直线与曲线有3个公共点时，实数的取值范围是      ． ‎ ‎32、类比“两角和与差的正余弦公式”的形式，对于给定的两个函数，，，其中，且，下面正确的运算公式是_______________.‎ ‎①；②；‎ ‎③；④；‎ ‎33、    已知二次函数的最小值为，且关于的一元二次不等式的解集为。    （Ⅰ）求函数的解析式；   ‎ ‎（Ⅱ）设其中，求函数在时的最大值；‎ ‎（Ⅲ）若（为实数），对任意，总存在使得成立，求实数的取值范围.‎ ‎34、     已知函数，且。（Ⅰ）求的值；‎ ‎（Ⅱ）判断并证明函数在区间上的单调性.‎ ‎35、已知函数的图象在上连续不断，定义：‎ ‎，。‎ 其中，表示函数在D上的最小值，表示函数在D上的最大值。若存在最小正整数，使得对任意的成立，则称函数为上的“阶收缩函数”。‎ ‎（1）若，试写出的表达式；‎ ‎（2）已知函数，试判断是否为上的“阶收缩函数”，  如果是，求出对应的；如果不是，请说明理由；‎ ‎（3）已知函数在上单调递增，在上单调递减，若 ‎    是上的“阶收缩函数”，求的取值范围。‎ ‎36、对定义在区间上的函数，若存在闭区间和常数，使得对任意的，都有，且对任意的都有恒成立，则称函数为区间上的“型”函数．‎ ‎（1）求证：函数是上的“型”函数；‎ ‎（2）设是（1）中的“型”函数，若不等式对一切的恒成立，求实数的取值范围；‎ ‎（3）若函数是区间上的“型”函数，求实数和的值．‎ ‎37、已知函数 [来源:学§科§网]‎ ‎     （1）若函数的最小值是,且,,‎ 求 的值；‎ ‎    （2）若,且在区间（0,1]上恒成立，试求b的取值范围.‎ ‎38、对于函数，若存在实数，使成立，则称为的不动点.‎ ‎   （1）当时，求的不动点；‎ ‎   （2）若对于任何实数，函数恒有两相异的不动点，求实数的取值范围；[来源:学科网]‎ ‎39、二次函数满足，其中．‎ ‎（1）判断的正负；（2）求证：方程在区间内恒有解． ‎ ‎40、已知关于的方程；‎ ‎（1）若该方程的一根在区间上，另一根在区间上，求实数的取值范围．[来源:学§科§网Z§X§X§K]‎ ‎（2）若该方程的两个根都在内且它们的平方和为1，求实数的取值集合． ‎ ‎1、 D2、B3、D 4、C 5、B6、D7、D8、、C  9、C 10、C11、D 12、D13、B        14、C ‎ ‎15、1【解析】由得，即，解得或。即，，所以，所以由图象可知要使直线与函数的图像有三个不同的交点，则有，即实数的取值范围是。不妨设，则由题意可知，所以，由得，所以，因为，所以，即存在最大值，最大值为1. ‎ ‎16、②③ ‎ ‎17、18、  ①③④  19、①②④20、①③④ 21、A ‎22、③④23、②③④24、【答案】③④25、 【解析】因为二次函数的值域为，所以有，且，即，所以，所以 ‎，当且仅当，即时取等号，所以最小值无。26、③⑤  27、  28、  29、 ‎ ‎30、 2、3 31、（0，1） ‎ ‎33‎ ‎34、‎ ‎35、     解：（1）由题意得：‎ ‎   （2），    ‎ ‎  当时，   当时，‎ ‎    当时， 综上所述：，又，则 ‎ ‎　 （3）ⅰ）时，在上单调递增，因此，，‎ ‎   。因为是上的“阶收缩函数”，所以，‎ ‎   ①对恒成立；  ②存在，使得成立。‎ ‎   ①即：对恒成立，由，解得：‎ ‎    ，要使对恒成立，需且只需 ‎   ②即：存在，使得成立。由得：‎ ‎   ，所以，需且只需 综合①②可得：‎ ‎  ⅱ）时，在上单调递增，在上单调递减，‎ ‎   因此，‎ ‎   显然当时，不成立。‎ ‎  ⅲ）当时，在上单调递增，在上单调递减 ‎   因此，‎ ‎   显然当时，不成立。   综合ⅰ）ⅱ）ⅲ）可得：[来源:学科网]‎ ‎36、（1）详见解析;（2）;（3）．‎ ‎∴ 或   ‎ ‎37、解：（1）由已知：c=1,a-b+c=0,-b/‎2a=-1,,a=1,b=2,f（x）=（x+1）‎ ‎     F（2）+F（-2）=（2+1）2+[-（-2+1）2]=8‎ ‎（2）原命题等价于在区间（0,1]上恒成立 即且在区间（0,1]上恒成立。又的最小值为0，的最大值为-2，∴‎ ‎38、解 ‎ ‎（1）当时，           设为其不动点，即 则    的不动点是－1，2. ‎ ‎（2）由得：.  由已知，此方程有相异二实根，恒成立，即即对任意恒成立.‎ ‎39、 ‎ ‎40、‎