高中数学选修2-3课件14_《独立性检验》 14页

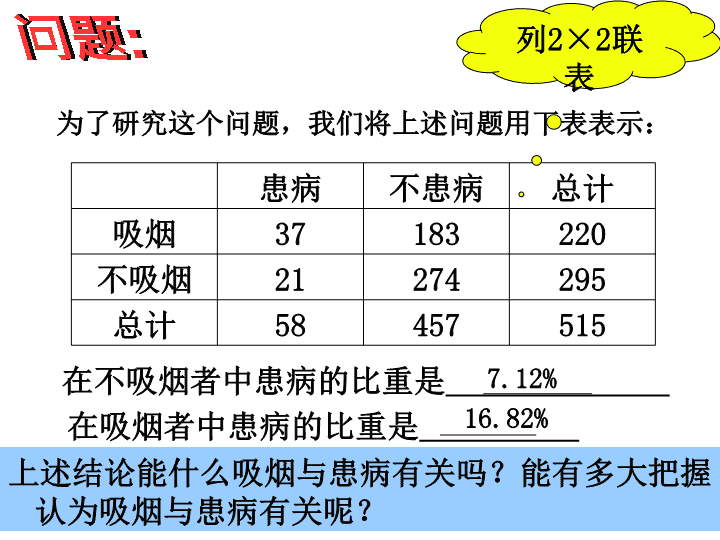
独立性检验 某医疗机构为了了解呼吸道疾病与吸烟是否有关，进行了一次抽样调查，共调查了 515 个成年人，其中吸烟者 220 人，不吸烟者 295 人，调查结果是：吸烟的 220 人中 37 人患 病 ， 183 人不患 病 ；不吸烟的 295 人中 21 人患 病 ， 274 人不患 病 。 根据这些数据能否断定：患肺癌与 吸烟有关吗？ 问题 : 患病 不患病 总计 吸烟 37 183 220 不吸烟 21 274 295 总计 58 457 515 问题 : 为了研究这个问题，我们将上述问题用下表表示： 列 2×2 联表 在不吸烟者中患病的比重是 在吸烟者中患病的比重是 7.12% 16.82% 上述结论能什么吸烟与患病有关吗？能有多大把握认为吸烟与患病有关呢？ 患病 不患病 总计 吸烟 a b a+b 不吸烟 c d c+d 总计 a+c b+d a+b+c+d 列出 2 ×2 列联表 假设 H 0 ： 吸烟和患病 之间没有关系 即 H 0 ： P(AB) ＝ P(A)P(B) 其中 A 为某人吸烟， B 为某人患病 设 n ＝ a ＋ b ＋ c ＋ d 则 P(A) P(B) 故 P(AB) 吸烟且患病人数 吸烟但未患病人数 不吸烟但患病人数 不吸烟且未患病人数 怎样描述实际观测值与估计值的差异呢？ 统计学中采用 即 独立性检验 第一步： H 0 ： 吸烟 和 患病 之间没有关系 通过数据和图表分析，得到结论是： 吸烟与患病有关 结论的可靠程度如何？ 患病 不患病 总计 吸烟 a b a+b 不吸烟 c d c+d 总计 a+c b+d a+b+c+d 第二步：列出 2 ×2 列联表 用 χ 2 统计量研究这类问题的方法 步骤 第三步：引入一个随机变量： 卡方统计量 第四步：查对临界值表，作出判断。 P( χ ≥x 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 x 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 P( χ ≥x 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 x 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 0.1% 把握认 为 A 与 B 无关 1% 把握认为 A 与 B 无关 99.9% 把握认 为 A 与 B 有关 99% 把握认 为 A 与 B 有关 90% 把握认 为 A 与 B 有关 10% 把握认为 A 与 B 无关 没有充分的依据显示 A 与 B 有关，但也不能显示 A 与 B 无关 例如 独立性检验 通过公式计算 患病 不患病 总计 吸烟 49 2099 2148 不吸烟 42 7775 7817 总计 91 9874 9965 H 0 ： 吸烟 和 患病 之间没有关系 解 ： 已知在 成立的情况下， 故有 99.9% 的把握认为 H 0 不成立，即有 99.9% 的把握认为 “ 患病与吸烟有关系 ” 。 即在 成立的情况下， 大于 10.828 概率非常小，近似为 0.001 现在的 =56.632 的观测值远大于 10.828 ，出现这样的观测值的概率不超过 0.001 。 反证法原理与假设检验原理 反证法原理： 在一个已知假设下，如果 推出一个矛盾 ，就 证明 了这个假设不成立。 假设检验原理： 在一个已知假设下，如果 一个与该假设矛盾的小概率事件发生 ， 就 推断 这个假设不成立。 例 1. 在 500 人身上试验某种血清预防感冒作用，把他们一年中的感冒记录与另外 500 名未用血清的人的感冒记录作比较，结果如表所示。问：该种血清能否起到预防感冒的作用？ 未感冒 感冒 合计 使用血清 258 242 500 未使用血清 216 284 500 合计 474 526 1000 解：设 H 0 ：感冒与是否使用该血清没有关系。 因当 H 0 成立时， χ 2 ≥6.635 的概率约为 0.01 ，故有 99% 的把握认为该血清能起到预防感冒的作用。 P(χ≥x 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 x 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 P(χ≥x 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 x 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 有效 无效 合计 口服 58 40 98 注射 64 31 95 合计 122 71 193 解：设 H 0 ：药的效果与给药方式没有关系。 因当 H 0 成立时， χ 2 ≥1.3896 的概率大于 15% ，故不能否定假设 H 0 ，即不能作出药的效果与给药方式有关的结论。 ＜ 2.072 例 2 ：为研究不同的给药方式（口服与注射）和药的效果（有效与无效）是否有关，进行了相应的抽样调查，调查的结果列在表中，根据所选择的 193 个病人的数据，能否作出药的效果和给药方式有关的结论？ P(χ≥x 0 ) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 x 0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 例 3 ：气管炎是一种常见的呼吸道疾病，医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比，所得数据如表所示，问：它们的疗效有无差异？ 有效 无效 合计 复方江剪刀草 184 61 245 胆黄片 91 9 100 合计 275 70 345 解：设 H 0 ：两种中草药的治疗效果没有差异。 因当 H 0 成立时， χ 2 ≥10.828 的概率为 0.001 ，故有 99.9% 的把握认为，两种药物的疗效有差异。