2021届浙江新高考数学一轮复习教师用书：第九章　2 第2讲　两直线的位置关系 15页

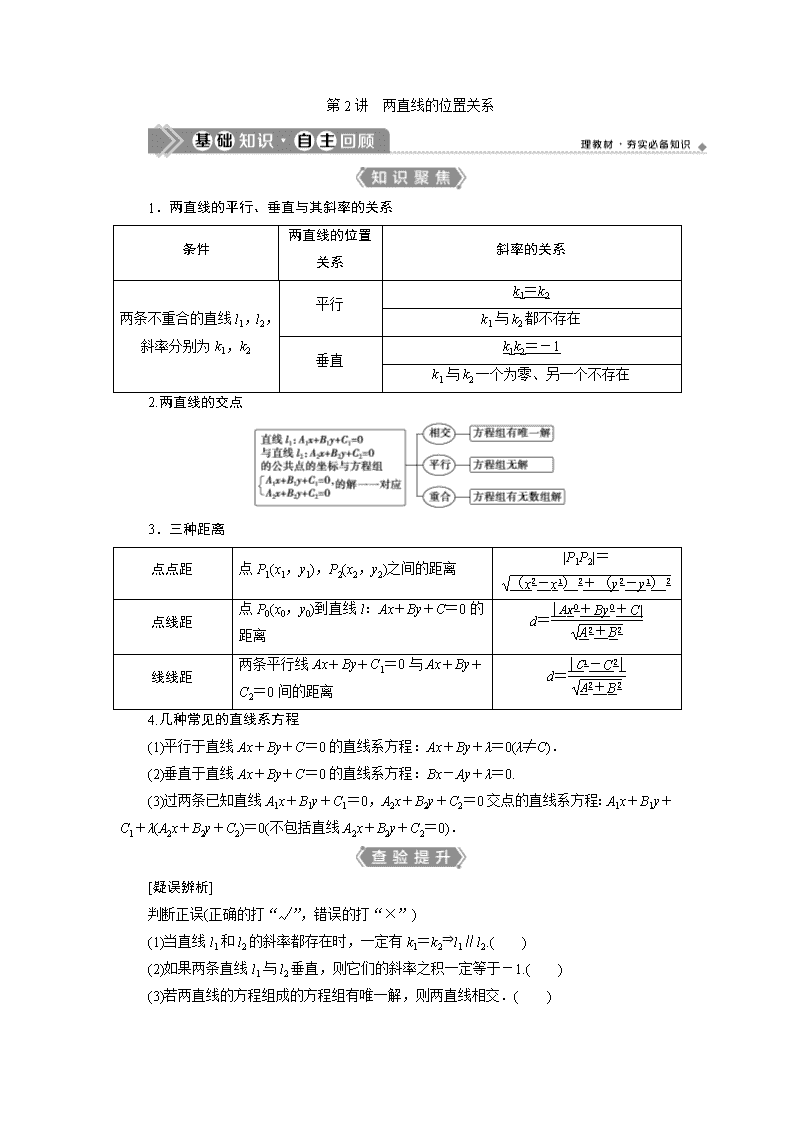
第2讲　两直线的位置关系 ‎1．两直线的平行、垂直与其斜率的关系 条件 两直线的位置关系 斜率的关系 两条不重合的直线l1，l2，斜率分别为k1，k2‎ 平行 k1＝k2‎ k1与k2都不存在 垂直 k1k2＝－1‎ k1与k2一个为零、另一个不存在 ‎2.两直线的交点 ‎3．三种距离 点点距 点P1(x1，y1)，P2(x2，y2)之间的距离 ‎|P1P2|＝ 点线距 点P0(x0，y0)到直线l：Ax＋By＋C＝0的距离 d＝ 线线距 两条平行线Ax＋By＋C1＝0与Ax＋By＋C2＝0间的距离 d＝ ‎4.几种常见的直线系方程 ‎(1)平行于直线Ax＋By＋C＝0的直线系方程：Ax＋By＋λ＝0(λ≠C)．‎ ‎(2)垂直于直线Ax＋By＋C＝0的直线系方程：Bx－Ay＋λ＝0.‎ ‎(3)过两条已知直线A1x＋B1y＋C1＝0，A2x＋B2y＋C2＝0交点的直线系方程：A1x＋B1y＋C1＋λ(A2x＋B2y＋C2)＝0(不包括直线A2x＋B2y＋C2＝0)．‎ ‎[疑误辨析]‎ 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)当直线l1和l2的斜率都存在时，一定有k1＝k2⇒l1∥l2.(　　)‎ ‎(2)如果两条直线l1与l2垂直，则它们的斜率之积一定等于－1.(　　)‎ ‎(3)若两直线的方程组成的方程组有唯一解，则两直线相交．(　　)‎ ‎(4)已知直线l1：A1x＋B1y＋C1＝0，l2：A2x＋B2y＋C2＝0(A1，B1，C1，A2，B2，C2为常数)，若直线l1⊥l2，则A1A2＋B1B2＝0.(　　)‎ ‎(5)直线外一点与直线上一点的距离的最小值就是点到直线的距离．(　　)‎ 答案：(1)×　(2)×　(3)√　(4)√　(5)√‎ ‎[教材衍化]‎ ‎1．(必修2P110B组T2改编)已知点(a，2)(a>0)到直线l：x－y＋3＝0的距离为1，则a＝________．‎ 解析：由题意得＝1.‎ 解得a＝－1＋或a＝－1－.因为a>0，所以a＝－1＋.‎ 答案：－1‎ ‎2．(必修2P101A组T10改编)已知P(－2，m)，Q(m，4)，且直线PQ垂直于直线x＋y＋1＝0，则m＝________．‎ 解析：由题意知＝1，所以m－4＝－2－m，所以m＝1.‎ 答案：1‎ ‎[易错纠偏]‎ (1)判断两直线平行时，忽视两直线重合的情况；‎ ‎(2)判断两直线的位置关系时，忽视斜率不存在的情况；‎ ‎(3)求两平行线间的距离，忽视x，y的系数应对应相同．‎ ‎1．直线2x＋(m＋1)y＋4＝0与直线mx＋3y－2＝0平行，则m＝________．‎ 解析：直线2x＋(m＋1)y＋4＝0与直线mx＋3y－2＝0平行，则有＝≠，故m＝2或－3.‎ 答案：2或－3‎ ‎2．若直线(3a＋2)x＋(1－4a)y＋8＝0与(5a－2)x＋(a＋4)y－7＝0垂直，则a＝________．‎ 解析：由两直线垂直的充要条件，得(3a＋2)(5a－2)＋(1－4a)(a＋4)＝0，解得a＝0或a＝1.‎ 答案：0或1‎ ‎3．直线2x＋2y＋1＝0，x＋y＋2＝0之间的距离是________．‎ 解析：先将2x＋2y＋1＝0化为x＋y＋＝0，‎ 则两平行线间的距离为d＝＝.‎ 答案： ‎　　　　　　两条直线平行与垂直 ‎ (2020·金丽衢十二校高三联考)设两直线l1：(3＋m)x＋4y＝5－3m与l2：2x＋(5＋m)y＝8，则“l1∥l2”是“m＜－1”的(　　)‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【解析】　若l1∥l2，则(3＋m)(5＋m)＝4×2⇒m＝－1或－7，经检验，当m＝－1时，l1与l2重合，‎ 所以m＝－7，故是充分不必要条件，故选A.‎ ‎【答案】　A 由一般式确定两直线位置关系的方法 直线方程 l1：A1x＋B1y＋C1＝0(A＋B≠0)‎ l2：A2x＋B2y＋C2＝0(A＋B≠0)‎ l1与l2垂直的充要条件 A1A2＋B1B2＝0‎ l1与l2平行的充分条件 ＝≠(A2B2C2≠0)‎ l1与l2相交的充分条件 ≠(A2B2≠0)‎ l1与l2重合的充分条件 ＝＝(A2B2C2≠0)‎ ‎　已知直线4x＋my－6＝0与直线5x－2y＋n＝0垂直，垂足为(t，1)，则n的值为(　　)‎ A．7　　　　　　　　　　　 B．9‎ C．11 D．－7‎ 解析：选A.由直线4x＋my－6＝0与直线5x－2y＋n＝0垂直得，20－2m＝0，m＝10.直线4x＋10y－6＝0过点(t，1)，所以4t＋10－6＝0，t＝－1.点(－1，1)又在直线5x－2y＋n＝0上，所以－5－2＋n＝0，n＝7.‎ ‎　　　　　　距离公式(高频考点)‎ 距离包括两点间、点到直线和两平行线间的距离．在高考中经常出现，试题难度不大．主要命题角度有：‎ ‎(1)求距离；‎ ‎(2)已知距离求参数值；‎ ‎(3)距离公式的综合应用．‎ 角度一　求距离 ‎ 已知A、B两点分别在两条互相垂直的直线2x－y＝0和x＋ay＝0上，且线段AB的中点为P(0，)，则线段AB的长为________．‎ ‎【解析】　依题意，a＝2，P(0，5)，设A(x，2x)、B(－2y，y)，故，则A(4，8)、B(－4，2)，‎ 所以|AB|＝＝10.‎ ‎【答案】　10‎ 角度二　已知距离求参数值 ‎ (1)已知点P(4，a)到直线4x－3y－1＝0的距离不大于3，则a的取值范围是(　　)‎ A．[－10，10] B．[－10，5]‎ C．[－5，5] D．[0，10]‎ ‎(2)若两平行直线3x－2y－1＝0，6x＋ay＋c＝0之间的距离为，则c的值是________．‎ ‎【解析】　(1)由题意得，点P到直线的距离为 ＝.‎ 又≤3，即|15－3a|≤15，‎ 解得0≤a≤10，所以a的取值范围是[0，10]．‎ ‎(2)依题意知，＝≠，‎ 解得a＝－4，c≠－2，‎ 即直线6x＋ay＋c＝0可化为3x－2y＋＝0，‎ 又两平行线之间的距离为，‎ 所以＝，‎ 因此c＝2或－6.‎ ‎【答案】　(1)D　(2)2或－6‎ 角度三　距离公式的综合应用 ‎ (1)P点在直线3x＋y－5＝0上，且P点到直线x－y－1＝0的距离为，则P点的坐标为(　　)‎ A．(1，2)‎ B．(2，1)‎ C．(1，2)或(2，－1)‎ D．(2，1)或(－1，2)‎ ‎(2)在△ABC中，A(1，1)，B(m，)(1