- 393.00 KB
- 2021-06-24 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
绝对值不等式的解法(一)
授课人:陈晓琳
一、知识联系
1
、绝对值的定义
|x|=
x ,x>0
-
x ,x<0
0 ,x=0
2
、绝对值的几何意义
0
x
|x|
x
1
x
|x
-
x
1
|
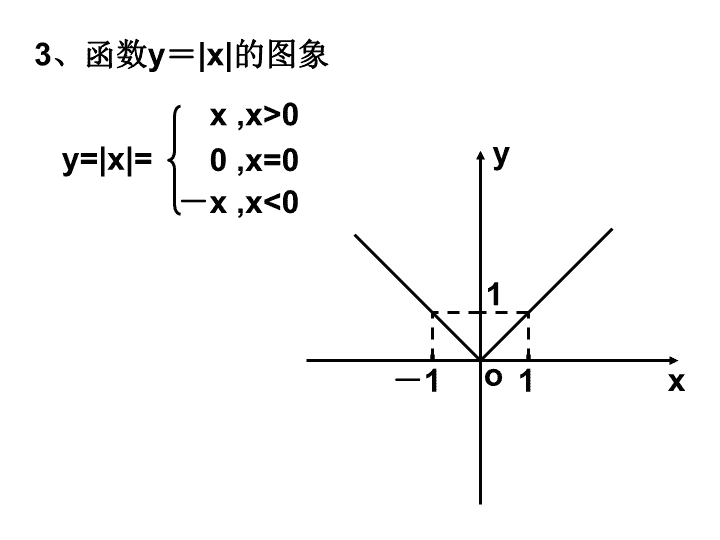
3
、函数
y
=
|x|
的图象
y=|x|=
x ,x>0
-
x ,x<0
0 ,x=0
o
x
y
1
1
-
1
二、探索解法
探索:不等式
|x|<1
的解集。
方法一:
利用绝对值的几何意义观察
方法二:
利用绝对值的定义去掉绝对值符号,需要分类讨论
方法三:
两边同时平方去掉绝对值符号
方法四:
利用函数图象观察
这是解含绝对值不等式的四种常用思路
1
2
3
4
0
-1
不等式
|x|<1
的解集表示到原点的距离小于
1
的点的集合。
1
所以,不等式
|x|<1
的解集为
{x|-1a (a>0)
的解集。
①
不等式
|x|a
的解集为
{x|x<-a
或
x>a }
0
-a
a
0
-a
a
基础练习:
解下列不等式:
(
1
)
|x|>5
(
2
)
2|x|<5
(
3
)
|2x|>5
(
4
)
|x-1|<5
(
5
)
|2x-1|<5
(
6
)
|2x
2
-x|<1
(
7
)
|2
x
-1|<1
1
-
4
6
(
4
)
|x-1|<5
(
5
)
|2x-1|<5
-
2
3
解下列不等式:
巩固练习:
(
8
)
| 6 - |2
x
+1| | >1
三、本节小结
本节课我们通过求不等式
|x|<1
的解集,得到了解含绝对值不等式的四种常用思路。
这四种思路将有助于我们有效地解决含绝对值不等式的问题。
方法一:
利用绝对值的几何意义观察
方法二:
利用绝对值的定义去掉绝对值符号,需要分类讨论
方法三:
两边同时平方去掉绝对值符号
方法四:
利用函数图象观察
谢谢!