高中数学 第三节 柯西不等式课件 新人教A版选修4-5 20页

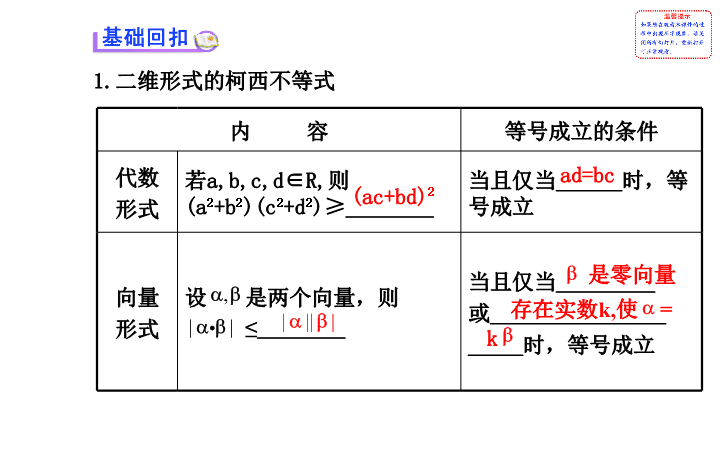
第三节 柯西不等式 1. 二维形式的柯西不等式 内 容 等号成立的条件 代数 形式 若 a,b,c,d ∈ R, 则 (a 2 +b 2 )(c 2 +d 2 ) ≥ ________ 当且仅当 ______ 时，等号成立 向量 形式 设 是两个向量，则 ≤ ________ 当且仅当 _________ 或 ________________ _____ 时， 等号成立 (ac+bd) 2 ad=bc 是零向量 存在实数 k, 使 = k 内 容 等号成立的条件 三角 形式 设 x 1 ,y 1 ,x 2 ,y 2 ∈R, 那么 _________________ 当且仅当 ___________________ _______________________________________ 时，等号成立 P 1 (x 1 ,y 1 ),P 2 (x 2 ,y 2 ), O(0,0) 三点共线，且 P 1 ， P 2 在原点 O 两旁 2. 三维形式的柯西不等式 设 a 1 ,a 2 ,a 3 ,b 1 ,b 2 ,b 3 ∈ R, 则 (a 1 2 +a 2 2 +a 3 2 )(b 1 2 +b 2 2 +b 3 2 ) ≥ _______________. 当且仅当 __________ 或 ___________________________________ 时 , 等号成立 . (a 1 b 1 +a 2 b 2 +a 3 b 3 ) 2 b 1 =b 2 =b 3 =0 存在一个数 k, 使得 a 1 =kb 1 ,a 2 =kb 2 ,a 3 =kb 3 3. 一般形式的柯西不等式 设 a 1 ,a 2 ,a 3 ,…,a n ,b 1 ,b 2 ,b 3 ,…,b n 是实数 , 则 (a 1 2 +a 2 2 +a 3 2 +…+a n 2 )(b 1 2 +b 2 2 +b 3 2 +…+b n 2 )≥ __________________________, 当且仅当 _________ __________ 或 ____________________________________ 时 , 等号成立 . (a 1 b 1 +a 2 b 2 +a 3 b 3 +…+a n b n ) 2 b i =0(i=1, 2,3,…,n) 存在一个数 k, 使得 a i =kb i (i=1,2,3,…,n) 判断下面结论是否正确 ( 请在括号中打“√”或“ ×”). (1) 在二维形式的柯西不等式的代数形式中，取等号的条件可 以是 ( ) (2) 在三维形式的柯西不等式中等号成立的条件是 ( ) (3) 设 是两个向量，则 中等号成立 的条件是存在实数 k ，使 ( ) 【 解析 】 (1) 错误 . 当 b ， d=0 时，柯西不等式成立，但 不成立 . (2) 错误 . 当 b 1 ,b 2 ,b 3 都为零时 , 不成立，但此时 柯西不等式成立 . (3) 错误 . 当 =0 时， 答案： (1)× (2)× (3)× 考向 1 二维柯西不等式代数形式的应用 【 典例 1】 设 a,b∈R + 且 a+b=2. 求证： 【 思路点拨 】 观察不等式的结构特点，本题可以看作求 的最小值，因而需出现柯西不等式的结构， 把 视为其中一个括号内的部分，另一部分可 以是 (2-a)+(2-b). 【 规范解答 】 根据柯西不等式， 有［ (2-a)+(2-b) ］ =(a+b) 2 =4, 当且仅当 即 a=b=1 时等号成立， ∴原不等式成立 . 【 拓展提升 】 正确理解二维柯西不等式 (1) 可以理解为四个有顺序的数对应的一种不等关系，或构造成一个不等式，如基本不等式是由两个数来构造的，但怎样构造要仔细体会 .(a 2 +b 2 )(c 2 +d 2 )≥(ac+bd) 2 ,(a 2 +b 2 )(d 2 +c 2 ) ≥(ad+bc) 2 , 谁与谁组合、联系，要有一定的认识 . (2) “ 二维 ” 是由向量的个数来说的，在平面上一个向量有两个量：横、纵坐标，因此 “ 二维 ” 就要有四个量，还可以认为是四个数组合成的一种不等关系 . (3) 根据题设条件，综合利用添、拆、分解、组合、配方、变量代换、数形结合等方法才能发现问题的本质，找到突破口 . 【 变式训练 】 已知 a 1 ,a 2 ,b 1 ,b 2 为正实数，求证 (a 1 b 1 +a 2 b 2 ) ≥(a 1 +a 2 ) 2 . 【 证明 】 对比柯西不等式的原型，两组数可取为： 则 (a 1 b 1 +a 2 b 2 ) =(a 1 +a 2 ) 2 . 当且仅当 即 b 1 =b 2 时等号成立 . 考向 2 利用柯西不等式求最值 【 典例 2】 (2013· 哈尔滨模拟 ) 已知 a,b,c∈(0,+∞), =2, 求 a+2b+3c 的最小值 . 【 思路点拨 】 分析待求式子的结构特征，结合已知条件构造两组数，利用柯西不等式求解 . 【 规范解答 】 =(1+2+3) 2 =36. 又 ∴ a+2b+3c≥18. 当且仅当 a=b=c=3 时等号成立 . 【 互动探究 】 本例条件不变，试求 4a+8b+27c 的最小值 . 【 解析 】 =(2+4+9) 2 =225, 又∵ ∴ 4a+8b+27c≥ 当且仅当 即 2a=2b=3c= 时取等号 . 即 4a+8b+27c 的最小值为 【 拓展提升 】 三维柯西不等式的应用 由 a,b,c 构成新的数字形式，而形成三维的柯西不等式，需要有较高的观察能力，从所给的数学式的结构中看出，常用的技巧有以下几种： (1) 构造符合柯西不等式的形式及条件可以巧拆常数 . (2) 构造符合柯西不等式的形式及条件可以重新安排各项的次序 . (3) 构造符合柯西不等式的形式及条件可以改变式子的结构 . (4) 构造符合柯西不等式的形式及条件可以添项 . 【 变式备选 】 (2013· 扬州模拟 ) 设 2x+3y+5z=29. 求函数 的最大值 . 【 解析 】 ≤ ［ (2x+1)+(3y+4)+(5z+6) ］ · (1+1+1) =3×(2x+3y+5z+11) =3×40=120. 故 当且仅当 2x+1=3y+4=5z+6, 即 时等号成立，此时