2018届二轮复习基本初等函数、函数与方程课件（全国通用） 27页

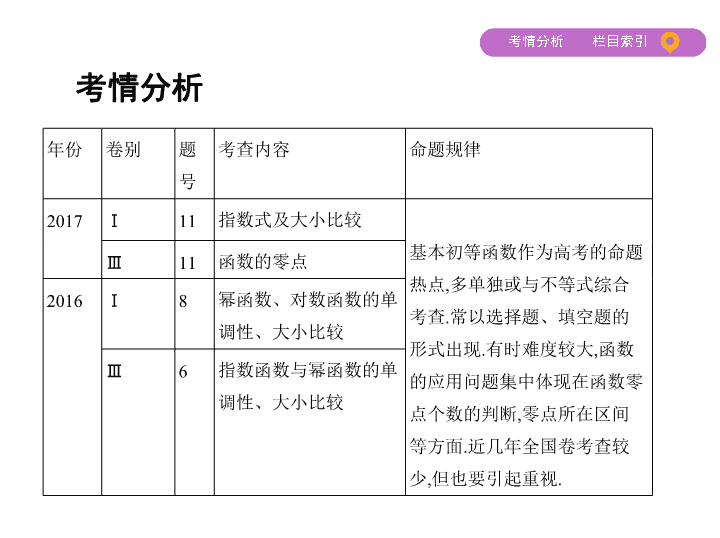
第 2 讲 基本初等函数、函数与方程 考情分析 年份 卷别 题号 考查内容 命题规律 2017 Ⅰ 11 指数式及大小比较 　　基本初等函数作为高考的命题热点,多单独或与不等式综合考查.常以选择题、填空题的形式出现.有时难度较大,函数的应用问题集中体现在函数零点个数的判断,零点所在区间等方面.近几年全国卷考查较少,但也要引起重视. Ⅲ 11 函数的零点 2016 Ⅰ 8 幂函数、对数函数的单调性、大小比较 Ⅲ 6 指数函数与幂函数的单调性、大小比较 总纲目录 考点一   基本初等函数的图象与性质 考点二 函数的零点（高频考点） 考点三 函数的实际应用 考点一    基本初等函数的图象与性质 指数函数与对数函数的图象与性质 指数函数 y = a x ( a >0且 a ≠ 1) 对数函数 y =log a x ( a >0且 a ≠ 1) 图象     单调性 0< a <1时,在R上单调递减; a >1时,在R上单调递增 0< a <1时,在(0,+ ∞ )上单调递减; a >1时,在(0,+ ∞ )上单调递增 函数值 0< a <1, 当 x >0时,0< y <1; 当 x <0时, y >1 0< a <1, 当 x >1时, y <0; 当0< x <1时, y >0 a >1, 当 x >0时, y >1; 当 x <0时,0< y <1 a >1, 当 x >1时, y >0; 当0< x <1时, y <0 典型例题 　　(1)(2017课标全国Ⅱ,8,5分)函数 f ( x )=ln( x 2 -2 x -8)的单调递增区间是   (　　) A.(- ∞ ,-2)　    B.(- ∞ ,1)　    C.(1,+ ∞ )　    D.(4,+ ∞ ) (2)(2017课标全国Ⅰ,11,5分)设 x , y , z 为正数,且2 x =3 y =5 z ,则       (　　) A.2 x <3 y <5 z 　    B.5 z <2 x <3 y C.3 y <5 z <2 x 　    D.3 y <2 x <5 z 解析 　(1)由 x 2 -2 x -8>0可得 x >4或 x <-2, 所以 x ∈(- ∞ ,-2) ∪ (4,+ ∞ ), 令 u = x 2 -2 x -8, 则其在 x ∈(- ∞ ,-2)上单调递减, 在 x ∈(4,+ ∞ )上单调递增. 又因为 y =ln u 在 u ∈(0,+ ∞ )上单调递增, 所以 y =ln( x 2 -2 x -8)在 x ∈(4,+ ∞ )上单调递增.故选D. 　　(2)由2 x =3 y =5 z ,可设(   ) 2 x =(   ) 3 y =(   ) 5 z = t , 因为 x , y , z 为正数,所以 t >1, 因为   =   =   ,   =   =   , 所以   <   ; 答案 　(1)D　(2)D 因为   =   =   ,   =   , 所以   >   ,所以   <   <   . 分别作出 y =(   ) x , y =(   ) x , y =(   ) x 的图象,如图.   则3 y <2 x <5 z ,故选D. 方法归纳 基本初等函数图象与性质的应用技巧 (1)对数函数与指数函数的单调性都取决于其底数的取值,当底数 a 的值 不确定时,要注意分 a >1和0< a <1两种情况讨论. (2)研究由指数函数、对数函数与其他函数复合而成的函数的性质,首 先通过换元法转化为两个或多个基本初等函数,然后根据复合函数的性 质与相关函数的性质之间的关系进行判断. (3)对于幂函数 y = x α 的性质要注意 α >0和 α <0两种情况的不同. 跟踪集训 1.已知函数 f ( x )=3 x - b (2 ≤ x ≤ 4, b 为常数)的图象经过点(2,1),则 f ( x )的值域为   (　　) A.[1,81]　    B.[1,3] C.[1,9]　    D.[1,+ ∞ ) 答案     C　由 f ( x )的图象过点(2,1),可知 b =2,∴ f ( x )=3 x -2 ,其在区间[2,4]上 是增函数,∴ f ( x ) min = f (2)=3 0 =1, f ( x ) max = f (4)=3 2 =9.故C正确. 2.(2017陕西高三教学质量检测试题(一))已知 a =   , b =(     , c =     ,则实数 a , b , c 的大小关系是   (　　) A. a > c > b 　    B. b > a > c C. a > b > c 　    D. c > b > a 答案     C　∵ a =   =   , b =(     =   =   , c =     =   (-cos x )   =   ,且0<   <   <2,∴ a > b > c ,故选C. 考点二    函数的零点(高频考点) 命题点 1.判断函数零点所在的区间. 2.判断函数零点的个数. 3.由函数零点的情况求参数的值(范围). 函数的零点与方程根、函数图象的关系 函数 F ( x )= f ( x )- g ( x )的零点就是方程 f ( x )= g ( x )的根,即函数 y = f ( x )的图象与 函数 y = g ( x )的图象交点的横坐标. 典型例题 　　(1)函数 f ( x )=   的零点个数是   (　　) A.0　    B.1　    C.2　    D.3 (2)(2017课标全国Ⅲ,11,5分)已知函数 f ( x )= x 2 -2 x + a (e x -1 +e - x +1 )有唯一零点, 则 a =   (　　) A.-   　    B.   　    C.   　    D.1 解析　(1)作出函数 f ( x )=   的图象,如图所示,   由图象可知,所求函数的零点个数是2. (2)由函数 f ( x )有零点得 x 2 -2 x + a (e x -1 +e - x +1 )=0有解,即( x -1) 2 -1+ a (e x -1 +e - x +1 )=0 有解, 令 t = x -1,则上式可化为 t 2 -1+ a (e t +e - t )=0,即 a =   . 答案 　(1)C　(2)C 令 h ( t )=   ,易得 h ( t )为偶函数, 又由 f ( x )有唯一零点得函数 h ( t )的图象与直线 y = a 有唯一交点,则此交点 的横坐标为0, 所以 a =   =   ,故选C. 方法归纳 判断函数零点个数的方法 跟踪集训 1.函数 f ( x )=log 3 x - x +2必有一个零点的区间是   (　　) A.   　    B.   C.   　    D.   答案     A　因为 f ( x )=log 3 x - x +2, 所以 f   =log 3   -   +2=-2-   +2=-   <0, f   =log 3   -   +2=-1-   +2=   >0, 即 f   · f   <0, 所以函数 f ( x )=log 3 x - x +2在   上必有一个零点. 2.(2017昆明教学质量检测)已知函数 f ( x )=   若存在实数 b ,使函 数 g ( x )= f ( x )- b 有两个不同的零点,则 a 的取值范围是 　　　     . 答案 　(2,4) 解析 　依题意,在同一平面直角坐标系内画出函数 y = x 2 与 y =2 x 的大致图 象(图略),要存在实数 b ,使得函数 g ( x )有两个不同的零点,即存在直线 y = b 与函数 y = f ( x )的图象有两个不同的交点,结合图象可知,实数 a 的取值范 围是(2,4). 考点三    函数的实际应用 应用函数模型解决实际问题的一般程序   ⇒   ⇒   ⇒   . 典型例题 (2017湖北七市(州)联考)某工厂产生的废气经过过滤后排放,过滤过程 中废气的污染物数量 P (毫克/升)与时间 t (小时)的关系为 P = P 0 e - kt .如果在 前5小时消除了10%的污染物,那么污染物减少19%需要花费的时间为 　　　     小时. 答案 　10 解析 　前5小时污染物消除了10%,此时污染物剩下90%,即 t =5时, P =0.9 P 0 ,代入,得(e - k ) 5 =0.9,∴e - k =   =0.   ,∴ P = P 0 e - kt = P 0 (0.   ) t .当污染物减少1 9%时,污染物剩下81%,此时 P =0.81 P 0 ,代入得0.81=(0.   ) t ,解得 t =10,即需 要花费10小时. 方法归纳 解决函数实际应用题的两个关键点 (1)认真读题,缜密审题,准确理解题意,明确问题的实际背景,然后进行科 学概括,将实际问题归纳为相应的数学问题. (2)要合理选取参数变量,设定变量之后,就要寻找它们之间的内在联系, 选用恰当的代数式表示问题中的关系,建立相应的函数模型,最终求解 函数模型使实际问题获解. 跟踪集训 1.国家规定某行业征税方法如下:年收入在280万元及以下的税率为 p %, 超过280万元的部分按( p +2)%征税,有一公司的实际缴税比例为( p +0.2 5)%,则该公司的年收入是   (　　) A.560万元　    B.420万元　    C.350万元　    D.320万元 答案     D　设该公司的年收入为 x ( x >280)万元,则有   =( p +0.25)%, 解得 x =320.故该公司的年收入为320万元. 2.某电脑公司在甲、乙两地各有一个分公司,甲地分公司现有某型号电 脑6台,乙地分公司现有同一型号的电脑12台.现 A 地某单位向该公司购 买该型号的电脑10台, B 地某单位向该公司购买该型号的电脑8台.已知 从甲地运往 A 、 B 两地每台电脑的运费分别是40元和30元.从乙地运 往 A 、 B 两地每台电脑的运费分别是80元和50元.若总运费不超过1 000 元,则调运方案的种数为   (　　) A.1　    B.2　    C.3　    D.4 答案     C　设总运费为 y 元,甲地调运 x 台电脑至 B 地,则剩下(6- x )台电脑 调运至 A 地,乙地应调运(8- x )台电脑至 B 地,调运12-(8- x )=( x +4)台电脑至 A 地(0 ≤ x ≤ 6, x ∈N). 则总运费 y =30 x +40(6- x )+50(8- x )+80( x +4)=20 x +960(0 ≤ x ≤ 6, x ∈N). 若 y ≤ 1 000,则20 x +960 ≤ 1 000,解得 x ≤ 2. 又0 ≤ x ≤ 6, x ∈N,∴0 ≤ x ≤ 2, x ∈N.∴ x =0,1,2,即有3种调运方案. 1.下列函数中,在(-1,1)内有零点且单调递增的是   (　　) A. y =log 2 x 　    B. y =2 x -1 C. y = x 2 -2　    D. y =- x 3 随堂检测 答案     B     y =log 2 x 在(-1,0]上没有意义,故A不满足题意; y = x 2 -2在(-1,0)上单调递减,故C不满足题意; y =- x 3 在(-1,1)上单调递减,故D不满足题意; ∵ y =2 x -1在(-1,1)上单调递增,且 f (-1)<0, f (1)>0,∴在(-1,1)内存在零点,故选B. 2.若函数 y = a | x | ( a >0,且 a ≠ 1)的值域为{ y |0< y ≤ 1},则函数 y =log a | x |的图象 大致是   (　　)   答案     A　若函数 y = a | x | ( a >0,且 a ≠ 1)的值域为{ y |0< y ≤ 1},则0< a <1,故函 数 y =log a | x |的大致图象是A. 3.某商场销售 A 型商品,已知该商品的进价是每件3元,且销售单价与日 均销售量的关系如表所示: 请根据以上数据分析,若要使该商品的日均销售利润最大,则此商品的 定价(单位:元/件)应为   (　　) A.4　    B.5.5　    C.8.5　    D.10 销售单价(元) 4 5 6 7 8 9 10 日均销售量 (件) 400 360 320 280 240 200 160 答案     C　由题意可设定价为 x 元/件,利润为 y 元,则 y =( x -3)[400-40( x -4)]= 40(- x 2 +17 x -42),故当 x =8.5时, y 有最大值,故选C. 4.已知函数 f ( x )=   则函数 g ( x )= f (1- x )-1的零点个数为   (　　) A.1　    B.2　    C.3　    D.4 答案     C　由题意得 g ( x )= f (1- x )-1=   即 g ( x )=   所以,当 x ≥ 1时,函数 g ( x )有一个零点, 当 x <1时,函数有两个零点, 所以函数 g ( x )= f (1- x )-1的零点共有3个,故选C. 5.计算:2log 4 10-   log 2 25+   -(π-3) 0 = 　　　     . 答案 　4 解析 　2log 4 10-   log 2 25+   -(π-3) 0 =2 ×   log 2 10-log 2 5+(2 3   -1=log 2   +2 2 -1= 1+4-1=4. 6.若函数 y =   - m 有两个零点,则 m 的取值范围是 　　　     . 答案 　(0,1) 解析 　在同一平面直角坐标系内,画出 y 1 =   和 y 2 = m 的图象,如图所示, 由于函数有两个零点,故0< m <1.