【数学】宁夏回族自治区银川一中2020届高三第三次模拟考试（理） 13页

宁夏回族自治区银川一中2020届高三第三次模拟考试（理）‎ ‎( 银川一中第三次模拟考试 )‎ 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2．作答时，务必将答案写在答题卡上。写在本试卷及草稿纸上无效。‎ ‎3．考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，则 A． B． C． D． ‎ ‎2．若复数z与其共轭复数满足，则 A． B． C．2 D． ‎ ‎3．抛物线的准线方程是 A． B． C． D． ‎ ‎4．若向量与平行，则 A． B． C． D． ‎ ‎5．已知是两条不重合的直线，是两个不重合的平面，则下列命题中，错误的是 A．若，则 B．若，则 C．若，则 D．若，则或 ‎ ‎6．已知函数y=f(x)的部分图像如图，则f(x)的解析式可能是 A． B． ‎ C． D． ‎ ‎7．为了加强“精准扶贫”，实现伟大复兴的“中国梦”，某大学派遣甲，乙，丙，丁，戊五位同学参加A,B,C三个贫困县的调研工作，每个县至少去1人，且甲，乙两人约定去同一个贫困县，则不同的派遣方案共有 A．24 B．‎36 ‎ C．48 D．64 ‎ ‎8．已知函数，，则的大小关系为 A． B． C． D． ‎ ‎9．天文学中，为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯（Hipparchus）在公元前二世纪首先提出了星等这个概念。星等的数值越小，星星就越亮；星等的数值越大它的光就越暗。到了1850年，由于光度计在天体光度测量的应用，英国天文学家普森（M.R.Pogson）又提出了衡量天体明暗程度的亮度的概念，天体的明暗程度可以用星等或亮度来描述。两颗星的星等与亮度满足，其中星等为的星的亮度为,已知“心宿二”的星等是1.00，“天津四”的星等是1.25，“心宿二”的亮度是“天津四”的倍，则与最接近的是（当较小时，）‎ A．1.24 B．‎1.25 ‎ C．1.26 D．1.27 ‎ ‎10．已知数列的通项公式是，其中 的部分图像如图所示，为数列的前项和，‎ 则的值为 A． B． C． D． ‎ ‎11．已知双曲线的右焦点为F，过F作直线的垂线，垂足为M，且交双曲线的左支于N点，若,则双曲线的离心率为 ‎ A． B． C．2 D． ‎ ‎12．已知函数，若函数有4个零点，则实数m的取值范围为 A． B． ‎ C． D． ‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13．我校高一、高二、高三共有学生1800名，为了了解同学们对“智慧课堂”的意见，计划采用分层抽样的方法，从这1800名学生中抽取一个样本容量为36的样本，若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数，则我校高三年级的学生人数为_____________ .‎ ‎14．已知实数x,y满足，则的最大值为_____________ .‎ ‎15．等差数列的前n项和为，,则_____________.‎ ‎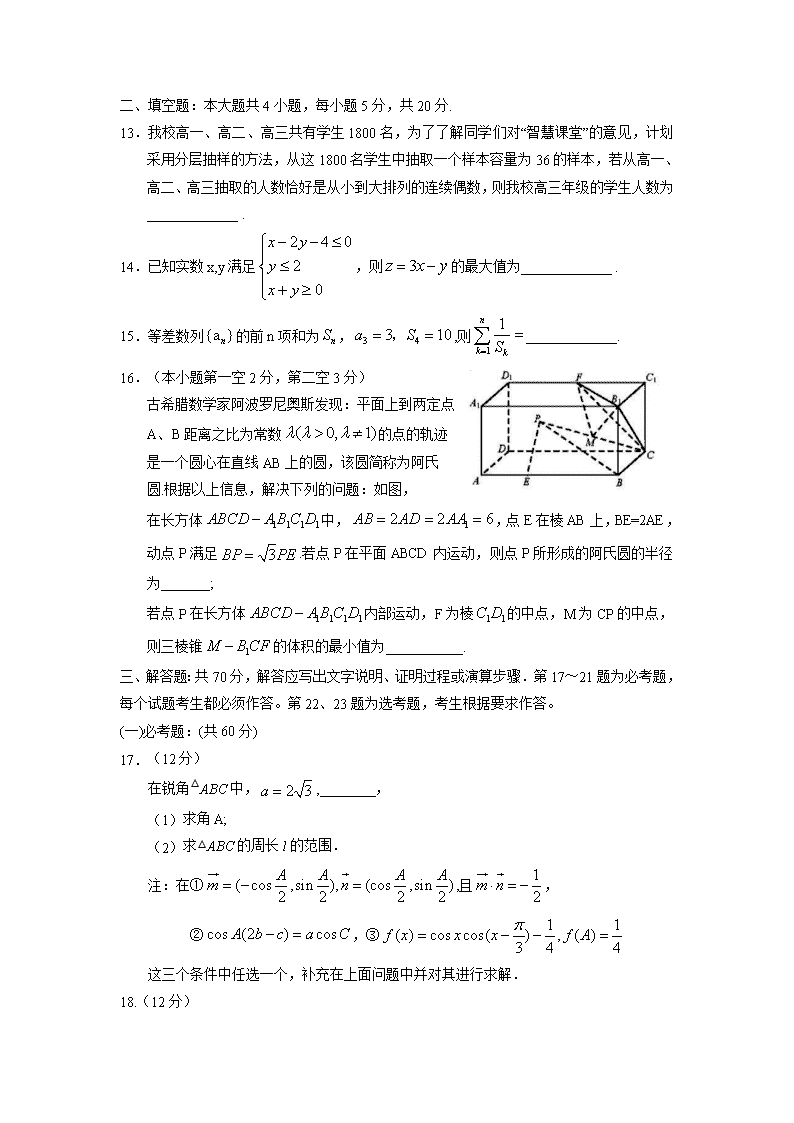16．（本小题第一空2分，第二空3分）‎ 古希腊数学家阿波罗尼奥斯发现：平面上到两定点 A、B距离之比为常数的点的轨迹 是一个圆心在直线AB上的圆，该圆简称为阿氏 圆.根据以上信息，解决下列的问题：如图，‎ 在长方体中，，点E在棱AB上，BE=2AE，动点P满足.若点P在平面ABCD内运动，则点P所形成的阿氏圆的半径为_______;‎ 若点P在长方体内部运动，F为棱的中点，M为CP的中点，则三棱锥的体积的最小值为___________.‎ 三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题：(共60分)‎ 17． ‎（12分）‎ 在锐角△ABC中，,________，‎ （1） 求角A;‎ （2） 求△ABC的周长l的范围．‎ 注：在①,且，‎ ‎②，③‎ 这三个条件中任选一个，补充在上面问题中并对其进行求解．‎ ‎18.（12分）‎ 在创建“全国文明城市”过程中，银川市“创城办”为了调查市民对创城工作的了解情况，进行了一次创城知识问卷调查（一位市民只能参加一次）通过随机抽样，得到参加问卷调查的100人的得分统计结果如表所示：‎ 组别 ‎[30,40)‎ ‎[40,50)‎ ‎[50,60)‎ ‎[60,70)‎ ‎[70,80)‎ ‎[80,90)‎ ‎[90,100]‎ 频数 ‎2‎ ‎13‎ ‎21‎ ‎25‎ ‎24‎ ‎11‎ ‎4‎ ‎（1）由频数分布表可以大致认为，此次问卷调查的得分Z∽N(μ，198)，μ近似为这100人得分的平均值（同一组中的数据用该组区间的左端点值作代表），①求μ的值；②利用该正态分布，求；‎ ‎（2）在（1）的条件下，“创城办”为此次参加问卷调查的市民制定如下奖励方案：‎ ‎①得分不低于的可以获赠2次随机话费，得分低于的可以获赠1次随机话费；‎ ‎②每次获赠的随机话费和对应的概率为：‎ 赠送话费的金额（单元：元）‎ ‎20‎ ‎50‎ 概率 现有市民甲参加此次问卷调查，记（单位：元）为该市民参加问卷调查获赠的话费，求的分布列与数学期望．‎ 参考数据与公式：‎ ‎．若X∽N ，则，，．‎ ‎19.(12分)‎ 如图,四棱锥中，，，，，．‎ ‎（1）求证：平面平面；‎ ‎（2）在线段上是否存在点，使得平面 与平面所成锐二面角为？若存在，求的值；‎ 若不存在，说明理由．‎ ‎20.（12分）‎ 已知函数 ‎（1）设，试讨论的单调性；‎ ‎（2）若函数在上有最大值，求实数a的取值范围 ‎21.（12分）‎ 已知O为坐标原点，椭圆C：的左，右焦点分别为,且又恰为抛物线D:的焦点，以为直径的圆与椭圆C仅有两个公共点.‎ ‎（1）求椭圆C的标准方程；‎ ‎（2）若直线与D相交于A,B两点，记点A,B到直线的距离分别为，，直线与C相交于E,F两点，记的面积分别为.‎ ‎ ①证明：的周长为定值；‎ ‎②求的最大值.‎ ‎（二）选考题：共10分.请考生在第22、23两题中任选一题做答，如果多做，则按所做的第一题记分.‎ ‎22．[选修4－4：坐标系与参数方程]‎ 在平面直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为，曲线的极坐标方程为.‎ ‎（1）写出直线和曲线的直角坐标方程；‎ ‎（2）已知点，若直线与曲线交于两点，中点为M，求的值.‎ ‎23．[选修4-5：不等式选讲]‎ 已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若，使得恒成立，求的取值范围.‎ 参考答案 一．选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D A D C A C B A C D B D 二、填空题：‎ ‎13、700 14、22 15、 16、（本小题第一空2分，第二空3分）‎ 三、解答题（解答应写出文字说明，证明过程或演算步骤）‎ ‎17．（1）若选①，∵，且 ‎（2） .........8分 ‎.............10分 ‎............11分 ‎.............12分 ‎（1）②∵cos A(2b-c)＝acos C ‎ ‎ ‎. .........6分 ‎（2） .........8分 ‎ ........10分 ‎ .........11分 ‎. .........12分 ‎（1）③‎ ‎＝cos2x＋cos xsin x－ ‎ ‎＝×＋×－ ‎ ........3分 ‎ .........5分 ‎. .........6分 ‎（2） .........8分 ‎ ........10分 ‎ .........11分 ‎. ........12分 ‎18.解（1）由题意得：‎ ‎∴，...........3分 ‎∵，‎ ‎...........6分 ‎（2）由题意知，...........7分 获赠话费的可能取值为20，40，50，70，100，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，...........10分 ‎∴的分布列为：‎ ‎ ‎ ‎ 20‎ ‎ 40‎ ‎ 50‎ ‎ 70‎ ‎ 100‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎...........11分 ‎∴．...........12分 ‎19.（1）证明：因四边形为直角梯形，‎ 且, ,,‎ 所以， ‎ 又因为。根据余弦定理得 ．...........2分 所以，故. ．...........3分 又因为, ,且,平面，所以平面，．...........4分 ‎ 又因平面PBC，所以...........5分 ‎（2）由（1）得平面平面, ‎ 设为的中点，连结 ，因为,‎ 所以,,又平面平面，‎ 平面平面，‎ 平面............6分 如图，以为原点分别以，和垂直平面的 方向为轴正方向，建立空间直角坐标系，‎ 则，，，，，‎ 假设存在满足要求，设，即，‎ 所以............7分 易得平面的一个法向量为. ............8分 设为平面的一个法向量，， ‎ 由得，不妨取.............9分 因为平面与平面所成的锐二面角为，所以，‎ 解得，（不合题意舍去）............11分 故存在点满足条件，且.............12分 ‎20.解析：‎ ‎（Ⅰ）‎ 令， ；.……………………………….1分 当时，，在上递增，无减区间.……….3分 当时，令，‎ 令 所以，在上单调递增，在上单调递减；.……………….5分 ‎（Ⅱ）由（Ⅰ）可知，当时，在上递增，‎ 在上递增，无最大值，不合题意；.……………………………….6分 当时，‎ 在上递减，，‎ 在上递减，无最大值，不合题意；.……………………………….7分 当时，，‎ 由（Ⅰ）可知在上单调递增，在上单调递减；.……….8分 设，则；‎ 令；令 在上单调递减，在单调递增；‎ ‎，即 由此，当时，，即．‎ 所以，当时，．‎ 取，则，且．‎ 又因为，所以由零点存在性定理，存在，使得；.……………………………….11分 当时，，即；当时，，即；‎ 所以，在上单调递增，在上单调递减，在上有最大值．‎ 综上，.……………………………….12分 ‎21.解（1）因为为抛物线D的焦点，故,所以c=1…………………….1分 又因为以为直径的圆与椭圆C仅有两个公共点知：b=c…………………….2分 所以，所以椭圆C的标准方程为…………………3分 （1） ‎①由题知，x=-1为抛物线D的准线，由抛物线的定义知：‎ ‎ 又因为,等号当且仅当三点共线时成立 所以直线过定点………………5分 由椭圆定义得：………………6分 ‎②若直线的斜率不存在，则直线的方程为x=1‎ 因为,所以………………7分 若直线斜率存在，则可设直线方程为，设 由得，，‎ 所以………………8分 由得，，设 则，‎ 所以……………10分 则 综上，的最大值等于……………12分 ‎22.解：（1）因为直线，故，‎ 即直线的直角坐标方程为.……………2分 因为曲线，则曲线的直角坐标方程为，即.………4分 ‎（2）设直线的参数方程为（为参数），‎ 将其代入曲线的直角坐标系方程得.‎ 设，对应的参数分别为，，则，， ……………6分 所以M对应的参数，……………8分 故……………10分 ‎23.解：（1）不等式可化为，‎ 当时，，，所以无解；……………1分 当时，，所以；……………2分 当时，，，所以.……………3分 综上，不等式的解集是.……………5分 ‎（2），‎ 又，使得恒成立，则，……………8分 ‎，解得.‎ 所以的取值范围为.……………10分