【数学】2021届一轮复习人教A版平面向量奔驰定理与三角形四心学案 4页

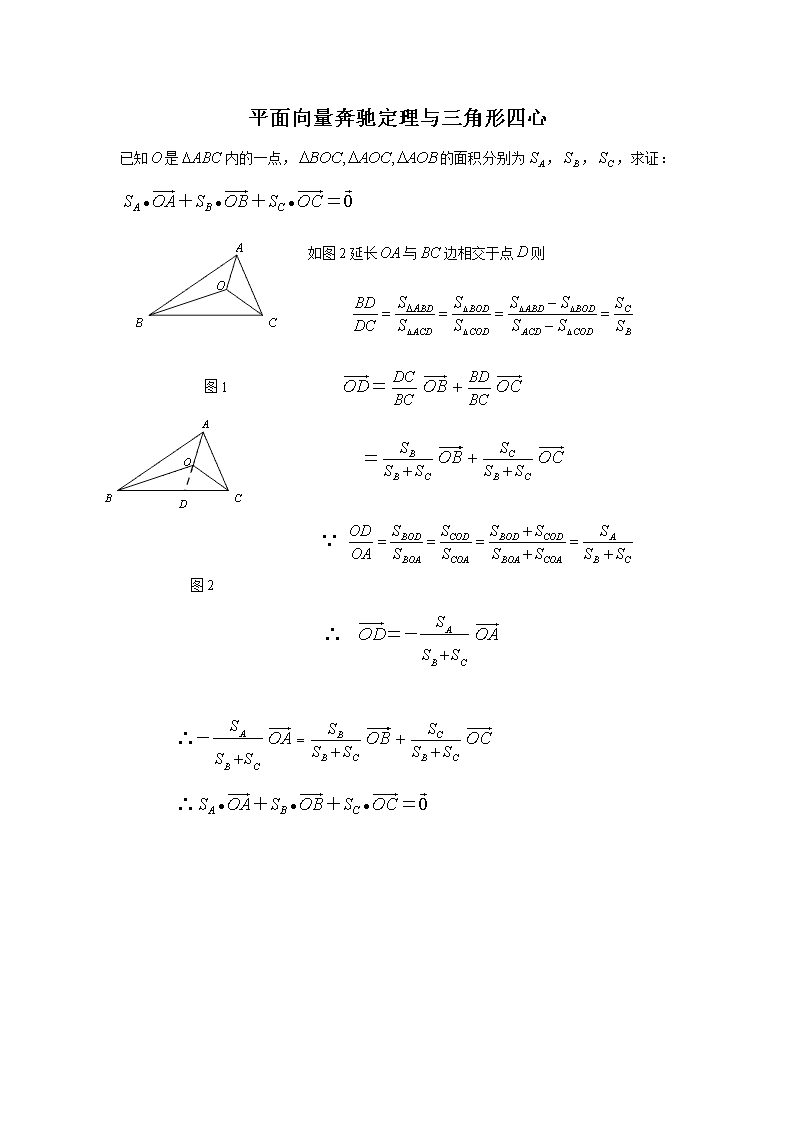
平面向量奔驰定理与三角形四心 已知是内的一点，的面积分别为，，，求证：‎ 如图2延长与边相交于点则 图1 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 图2‎ ‎ ‎ ‎ ‎ 推论:是内的一点，且，则 有此定理可得三角形四心向量式 ‎1、是的重心 ‎2、是的内心 ‎3、是的外心 ‎4、是的垂心 ‎ ‎ 证明：如图为三角形的垂心，‎ 同理得，‎ 奔驰定理是三角形四心向量式的完美统一 三角形“四心”的相关向量问题 四心的概念介绍：‎ ‎(1) 重心：中线的交点，重心将中线长度分成2：1；‎ ‎(2) 垂心：高线的交点，高线与对应边垂直；‎ ‎(3) 内心：角平分线的交点（内切圆的圆心），角平分线上的任意点到角两边的距离相等；‎ ‎(4) 外心：中垂线的交点（外接圆的圆心），外心到三角形各顶点的距离相等。‎ l 与“重心”有关的向量问题 ‎1． 已知是所在平面上的一点，若，则是的( )．‎ A．重点 B．外心 C．内心 D．垂心 ‎2．已知是平面上一定点，是平面上不共线的三个点，动点满足，，则的轨迹一定通过的( ).‎ A．重点 B．外心 C．内心 D．垂心 ‎3 .O是△ABC所在平面内一点，动点P满足（λ∈（0，+∞）），则动点P的轨迹一定通过△ABC的（　　）‎ A．内心 B．重心 C．外心 D．垂心 l 与“垂心”有关的向量问题 ‎4.是所在平面上一点，若，则是的( )‎ A．重点 B．外心 C．内心 D．垂心 ‎5.已知是平面上一定点，是平面上不共线的三个点，动点满足，，则动点的轨迹一定通过的( )．‎ A．重点 B．外心 C．内心 D．垂心 ‎6.若为所在平面内一点，且 则点是的( )‎ A．重点 B．外心 C．内心 D．垂心 l 与“内心”有关的向量问题 ‎7.已知是平面上一定点，是平面上不共线的三个点，动点满足 ‎ ，，则动点的轨迹一定通过的( )．‎ A．重点 B．外心 C．内心 D．垂心 ‎8.若O在△ABC所在的平面内：=，则O是△ABC的（　　）‎ A．垂心 B．重心 C．内心 D．外心 l 与“外心”有关的向量问题 ‎9.已知是所在平面上一点，若，则是的( )．‎ A．重点 B．外心 C．内心 D．垂心 ‎10.已知是平面上的一定点，是平面上不共线的三个点，动点满足，，则动点的轨迹一定通过的( )。‎ A．重点 B．外心 C．内心 D．垂心