【数学】2018届一轮复习人教A版（文）集合与常用逻辑用语教案 34页

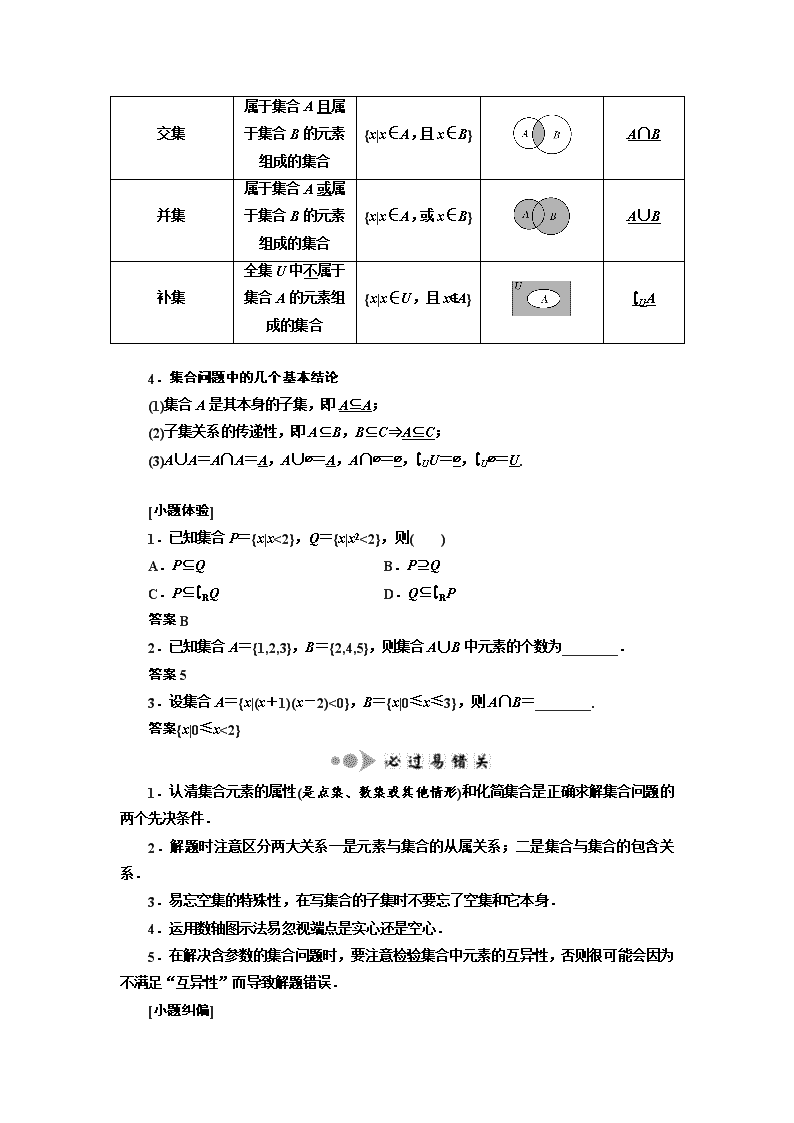
第一章集合与常用逻辑用语 第一节集__合 ‎1．集合的相关概念 ‎(1)集合元素的三个特性确定性、无序性、互异性．‎ ‎(2)元素与集合的两种关系属于，记为∈；不属于，记为∉.‎ ‎(3)集合的三种表示方法列举法、描述法、图示法．‎ ‎(4)五个特定的集合 集合 自然数集 正整数集 整数集 有理数集 实数集 符号 N N*或N＋‎ Z Q R ‎2．集合间的基本关系 ‎　　表示 关系　　‎ 文字语言 符号语言 记法 基本关系 子集 集合A的元素都是集合B的元素 x∈A⇒‎ x∈B A⊆B或B⊇A 真子集 集合A是集合B的子集，且集合B中至少有一个元素不属于A A⊆B，且∃x0∈B，x0∉A AB或 BA 相等 集合A，B的元素完全相同 A⊆B，‎ B⊆A A＝B 空集 不含任何元素的集合．空集是任何集合A的子集 ‎∀x，x∉∅，∅⊆A ‎∅‎ ‎3．集合的基本运算 ‎　 表示 运算 　‎ 文字语言 符号语言 图形语言 记法 交集 属于集合A且属于集合B的元素组成的集合 ‎{x|x∈A，且x∈B}‎ A∩B 并集 属于集合A或属于集合B的元素组成的集合 ‎{x|x∈A，或x∈B}‎ A∪B 补集 全集U中不属于集合A的元素组成的集合 ‎{x|x∈U，且x∉A}‎ ‎∁UA ‎4．集合问题中的几个基本结论 ‎(1)集合A是其本身的子集，即A⊆A；‎ ‎(2)子集关系的传递性，即A⊆B，B⊆C⇒A⊆C；‎ ‎(3)A∪A＝A∩A＝A，A∪∅＝A，A∩∅＝∅，∁UU＝∅，∁U∅＝U.‎ ‎[小题体验]‎ ‎1．已知集合P＝{x|x<2}，Q＝{x|x2<2}，则(　　)‎ A．P⊆Q　　　　　　　　 B．P⊇Q C．P⊆∁RQ D．Q⊆∁RP 答案B ‎2．已知集合A＝{1,2,3}，B＝{2,4,5}，则集合A∪B中元素的个数为________．‎ 答案5‎ ‎3．设集合A＝{x|(x＋1)(x－2)<0}，B＝{x|0≤x≤3}，则A∩B＝________.‎ 答案{x|0≤x<2}‎ ‎1．认清集合元素的属性(是点集、数集或其他情形)和化简集合是正确求解集合问题的两个先决条件．‎ ‎2．解题时注意区分两大关系一是元素与集合的从属关系；二是集合与集合的包含关系．‎ ‎3．易忘空集的特殊性，在写集合的子集时不要忘了空集和它本身．‎ ‎4．运用数轴图示法易忽视端点是实心还是空心．‎ ‎5．在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致解题错误．‎ ‎[小题纠偏]‎ ‎1．设全集U＝R，集合A＝{x|7－6x≤0}，集合B＝{x|y＝lg(x＋2)}，则(∁UA)∩B等于(　　)‎ A. B. C. D. 解析选A　依题意得A＝，∁UA＝；B＝{x|x＋2>0}＝{x|x>－2}，因此(∁UA)∩B＝.‎ ‎2．已知集合A＝{x∈N|x2－2x≤0}，则满足A∪B＝{0,1,2}的集合B的个数为________．‎ 解析由A中的不等式解得0≤x≤2，x∈N，即A＝{0,1,2}．∵A∪B＝{0,1,2}，∴B可能为{0}，{1}，{2}，{0,1}，{0,2}，{1,2}，{0,1,2}，∅，共8个．‎ 答案8‎ ‎3．已知集合A＝{0,1，x2－5x}，若－4∈A，则实数x的值为________．‎ 解析∵－4∈A，∴x2－5x＝－4，‎ ‎∴x＝1或x＝4.‎ 答案1或4‎ ‎[题组练透]‎ ‎1．(易错题)已知集合A＝{1,2,4}，则集合B＝{(x，y)|x∈A，y∈A}中元素的个数为(　　)‎ A．3　　　　　　　　　 B．6‎ C．8 D．9‎ 解析选D　集合B中元素有(1,1)，(1,2)，(1,4)，(2,1)，(2,2)，(2,4)，(4,1)，(4,2)，(4,4)，共9个．‎ ‎2．已知a，b∈R，若＝{a2，a＋b,0}，则a2 017＋b2 017为(　　)‎ A．1 B．0‎ C．－1 D．±1‎ 解析选C　由已知得a≠0，则＝0，所以b＝0，于是a2＝1，即a＝1或a＝－1，又根据集合中元素的互异性可知a＝1应舍去，因此a＝－1，故a2 017＋b2 017＝(－1)2 017＋02 017＝－1.‎ ‎3．若集合A＝{x∈R|ax2－3x＋2＝0}中只有一个元素，则a等于(　　)‎ A. B. C．0 D．0或 解析选D　若集合A中只有一个元素，则方程ax2－3x＋2＝0只有一个实根或有两个相等实根．‎ 当a＝0时，x＝，符合题意．‎ 当a≠0时，由Δ＝(－3)2－‎8a＝0，得a＝，‎ 所以a的值为0或.‎ ‎4．(易错题)已知集合A＝{m＋2,‎2m2‎＋m}，若3∈A，则m的值为________．‎ 解析由题意得m＋2＝3或‎2m2‎＋m＝3，则m＝1或m＝－，当m＝1时，m＋2＝3且‎2m2‎＋m＝3，根据集合中元素的互异性可知不满足题意；当m＝－时，m＋2＝，而‎2m2‎＋m＝3，故m＝－.‎ 答案－ ‎[谨记通法]‎ 与集合中的元素有关问题的求解策略 ‎(1)确定集合的元素是什么，即集合是数集还是点集．如“题组练透”第1题．‎ ‎(2)看这些元素满足什么限制条件．‎ ‎(3)根据限制条件列式求参数的值或确定集合中元素的个数，但要注意检验集合是否满足元素的互异性．如“题组练透”第4题．‎ ‎[典例引领]‎ ‎1．已知集合M＝{1,2,3,4}，则集合P＝{x|x∈M且2x∉M}的子集有(　　)‎ A．8个　　　　　　　　 B．4个 C．3个 D．2个 解析选B　由题意，得P＝{3,4}，所以集合P的子集有22＝4个．‎ ‎2．已知集合A＝{x|y＝，x∈R}，B＝{x|x＝m2，m∈A}，则(　　)‎ A．AB B．BA C．A⊆B D．B＝A 解析选B　由题意知A＝{x|y＝，x∈R}，所以A＝{x|－1≤x≤1}．所以B＝{x|x＝m2，m∈A}＝{x|0≤x≤1}，所以BA，故选B.‎ ‎[由题悟法]‎ 集合间基本关系的两种判定方法和一个关键 ‎[即时应用]‎ ‎1．已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0＜x＜5，x∈N}，则满足条件A⊆C⊆B的集合C的个数为(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析选D　由x2－3x＋2＝0得x＝1或x＝2，‎ ‎∴A＝{1,2}．‎ 由题意知B＝{1,2,3,4}，∴满足条件的C可为{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}．‎ ‎2．已知集合A＝{x|－10时，∵A＝{x|－11}，若A∩B＝A，则a的取值范围是(　　)‎ A．[5，＋∞) B．[4，＋∞)‎ C．(－∞，－5) D．(－∞，4)‎ 解析选B　B＝，由A∩B＝A⇒A⊆B，‎ ‎∴≤－1，解得a≥4.‎ 角度三新定义集合问题 ‎4.设A,B是非空集合，定义AB={x|x∈A∪B且xA∩B}已知集合A={x|00}，则A∩B＝(　　)‎ A.　　　　　　 B. C. D. 解析选D　∵x2－4x＋3<0，∴10，∴x>，∴B＝.‎ ‎∴A∩B＝{x|10}，则AB为(　　)‎ A．{x|02}‎ 解析选D　因为A＝{x|0≤x≤2}，B＝{y|y>1}，A∪B＝{x|x≥0}，A∩B＝{x|12}，故选D.‎ ‎4．(2017·湖北七市(州)协作体联考)已知集合P＝{n|n＝2k－1，k∈N*，k≤50}，Q＝{2,3,5}，则集合T＝{xy|x∈P，y∈Q}中元素的个数为(　　)‎ A．147 B．140‎ C．130 D．117‎ 解析选B　由题意得，y的取值一共有3种情况，当y＝2时，xy是偶数，不与y＝3，y＝5时有相同的元素，当y＝3，x＝5,15,25，…，95时，与y＝5，x＝3,9,15，…，57时有相同的元素，共10个，故所求元素个数为3×50－10＝140，故选B.‎ 一抓基础，多练小题做到眼疾手快 ‎1．(2016·全国甲卷)已知集合A＝{1,2,3}，B＝{x|(x＋1)(x－2)<0，x∈Z}，则A∪B＝(　　)‎ A．{1}　　　　　　　　　 B．{1,2}‎ C．{0,1,2,3} D．{－1,0,1,2,3}‎ 解析选C　因为B＝{x|(x＋1)(x－2)<0，x∈Z}＝{x|－10}，则下列结论正确的是(　　)‎ A．M⊆N B．M⊆(∁RN)‎ C．(∁RM)⊆N D．(∁RM)⊆(∁RN)‎ 解析选B　由题意，得N＝{x|x<－1或x>3}，‎ 所以∁RN＝{x|－1≤x≤3}，又M＝{x|0≤x≤2}，‎ 所以M是∁RN的子集，故选B.‎ ‎3．(2017·中原名校联考)设全集U＝R，集合A＝{x|0≤x≤2}，B＝{y|1≤y≤3}，则(∁UA)∪B＝(　　)‎ A．(2,3]‎ B．(－∞，1]∪(2，＋∞)‎ C．[1,2)‎ D．(－∞，0)∪[1，＋∞)‎ 解析选D　因为∁UA＝{x|x>2或x<0}，B＝{y|1≤y≤3}，所以(∁UA)∪B＝(－∞，0)∪[1，＋∞)．‎ ‎4．(2017·河南六市第一次联考)已知集合A＝{x|x2－3x<0}，B＝{1，a}，且A∩B有4个子集，则实数a的取值范围是(　　)‎ A．(0,3) B．(0,1)∪(1,3)‎ C．(0,1) D．(－∞，1)∪(3，＋∞)‎ 解析选B　∵A∩B有4个子集，∴A∩B中有2个不同的元素，∴a∈A，∴a2－‎3a<0，解得0m＋2}，‎ 因为A⊆∁RB，‎ 所以m－2>3或m＋2<－1，‎ 即m>5或m<－3.‎ 因此实数m的取值范围是(－∞，－3)∪(5，＋∞)．‎ 三上台阶，自主选做志在冲刺名校 ‎1．已知集合A＝{x|x2－2 017x＋2 016<0}，B＝{x|log2xy2，则x>y”的逆否命题是________．‎ 答案“若x≤y，则x2≤y‎2”‎ ‎1．易混淆否命题与命题的否定否命题是既否定条件，又否定结论，而命题的否定是只否定命题的结论．‎ ‎2．易忽视A是B的充分不必要条件(A⇒B且B A)与A的充分不必要条件是B(B⇒A且A B)两者的不同．‎ ‎[小题纠偏]‎ ‎1．设a，b均为非零向量，则“a∥b”是“a与b的方向相同”的________条件．‎ 答案必要不充分 ‎2．“在△ABC中，若∠C＝90°，则∠A，∠B都是锐角”的否命题为________________.‎ 解析原命题的条件在△ABC中，∠C＝90°，‎ 结论∠A，∠B都是锐角．否命题是否定条件和结论．‎ 即“在△ABC中，若∠C≠90°，则∠A，∠B不都是锐角”．‎ 答案在△ABC中，若∠C≠90°，则∠A，∠B不都是锐角 ‎[题组练透]‎ ‎1．命题“若a2>b2，则a>b”的否命题是(　　)‎ A．若a2>b2，则a≤b　　 B．若a2≤b2，则a≤b C．若a≤b，则a2>b2 D．若a≤b，则a2≤b2‎ 解析选B　根据命题的四种形式可知，命题“若p，则q”的否命题是“若綈p，则綈q”．该题中，p为a2>b2，q为a>b，故綈p为a2≤b2，綈q为a≤b.所以原命题的否命题为若a2≤b2，则a≤b.‎ ‎2．命题“若x2＋3x－4＝0，则x＝‎4”‎的逆否命题及其真假性为(　　)‎ A．“若x＝4，则x2＋3x－4＝‎0”‎为真命题 B．“若x≠4，则x2＋3x－4≠‎0”‎为真命题 C．“若x≠4，则x2＋3x－4≠‎0”‎为假命题 D．“若x＝4，则x2＋3x－4＝‎0”‎为假命题 解析选C　根据逆否命题的定义可以排除A，D，因为x2＋3x－4＝0，所以x＝4或－1，故原命题为假命题，即逆否命题为假命题．‎ ‎3．给出以下四个命题 ‎①“若x＋y＝0，则x，y互为相反数”的逆命题；‎ ‎②(易错题)“全等三角形的面积相等”的否命题；‎ ‎③“若q≤－1，则x2＋x＋q＝0有实根”的逆否命题；‎ ‎④若ab是正整数，则a，b都是正整数．‎ 其中真命题是________．(写出所有真命题的序号)‎ 解析①命题“若x＋y＝0，则x，y互为相反数”的逆命题为“若x，y互为相反数，则x＋y＝‎0”‎，显然①为真命题；②不全等的三角形的面积也可能相等，故②为假命题；③原命题正确，所以它的逆否命题也正确，故③为真命题；④若ab是正整数，但a，b不一定都是正整数，例如a＝－1，b＝－3，故④为假命题．‎ 答案①③‎ ‎[谨记通法]‎ ‎1．写一个命题的其他三种命题时的2个注意点 ‎(1)对于不是“若p，则q”形式的命题，需先改写；‎ ‎(2)若命题有大前提，写其他三种命题时需保留大前提．如“题组练透”第3题②易忽视．‎ ‎2．命题真假的2种判断方法 ‎(1)联系已有的数学公式、定理、结论进行正面直接判断．‎ ‎(2)利用原命题与逆否命题，逆命题与否命题的等价关系进行判断．‎ ‎[典例引领]‎ ‎1．(2015·北京高考)设a，b是非零向量，“a·b＝|a||b|”是“a∥b”的(　　)‎ A．充分而不必要条件　　 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 解析选A　a·b＝|a||b|cos〈a，b〉．而当a∥b时，〈a，b〉还可能是π，此时a·b＝－|a||b|，故“a·b＝|a||b|”是“a∥b”的充分而不必要条件．‎ ‎2．(2017·衡阳联考)设px2－x－20>0，qlog2(x－5)<2，则p是q的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 解析选B　∵x2－x－20>0，∴x>5或x<－4，∴px>5或x<－4.∵log2(x－5)<2，∴05或x<－4}，∴p是q的必要不充分条件．故选B.‎ ‎[由题悟法]‎ 充要条件的3种判断方法 ‎(1)定义法根据p⇒q，q⇒p进行判断；‎ ‎(2)集合法根据p，q成立的对象的集合之间的包含关系进行判断；‎ ‎(3)等价转化法根据一个命题与其逆否命题的等价性，把判断的命题转化为其逆否命题进行判断．这个方法特别适合以否定形式给出的问题，如“xy≠‎1”‎是“x≠1或y≠‎1”‎的某种条件，即可转化为判断“x＝1且y＝‎1”‎是“xy＝‎1”‎的某种条件．‎ ‎[即时应用]‎ ‎1．(2016·天津高考)设x＞0，y∈R，则“x＞y”是“x＞|y|”的(　　)‎ A．充要条件 B．充分而不必要条件 C．必要而不充分条件 D．既不充分也不必要条件 解析选C　当x＝1，y＝－2时，x＞y，但x＞|y|不成立；若x＞|y|，因为|y|≥y，所以x＞y.所以x＞y是x＞|y|的必要而不充分条件．‎ ‎2．已知条件px＋y≠－2，条件qx，y不都是－1，则p是q的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 解析选A　因为px＋y≠－2，qx≠－1，或y≠－1，‎ 所以綈px＋y＝－2，綈qx＝－1，且y＝－1，‎ 因为綈q⇒綈p但綈p綈q，所以綈q是綈p的充分不必要条件，即p是q的充分不必要条件．‎ ‎[典例引领]‎ ‎1．(2017·皖北第一次联考)已知px≥k，q<1，如果p是q的充分不必要条件，则实数k的取值范围是(　　)‎ A．[2，＋∞)　　　　　 B．(2，＋∞)‎ C．[1，＋∞) D．(－∞，－1)‎ 解析选B　∵<1，∴－1＝<0，即(x－2)(x＋1)>0，∴x>2或x<－1，∵p是q的充分不必要条件，∴k>2.‎ ‎2．设n∈N*，一元二次方程x2－4x＋n＝0有整数根的充要条件是n＝________.‎ 解析由Δ＝16－4n≥0，得n≤4，又n∈N*，则n＝1,2,3,4.当n＝1,2时，方程没有整数根，当n＝3时，方程有整数根1,3，当n＝4时，方程有整数根2，综上知n＝3或4.‎ 答案3或4‎ ‎[由题悟法]‎ 根据充要条件求参数的值或取值范围的关键点 ‎(1)先合理转化条件，常通过有关性质、定理、图象将恒成立问题和有解问题转化为最值问题等，得到关于参数的方程或不等式(组)，再通过解方程或不等式(组)求出参数的值或取值范围．‎ ‎(2)求解参数的取值范围时，一定要注意区间端点值的检验，尤其是利用两个集合之间的关系求解参数的取值范围时，不等式是否能够取等号决定端点值的取舍，处理不当容易出现漏解或增解的现象．[即时应用]‎ ‎1．已知命题px2＋2x－3>0；命题qx>a，且綈q的一个充分不必要条件是綈p，则a的取值范围是(　　)‎ A．[1，＋∞) B．(－∞，1]‎ C．[－1，＋∞) D．(－∞，－3]‎ 解析选A　由x2＋2x－3>0，得x<－3或x>1，由綈q的一个充分不必要条件是綈p，可知綈p是綈q的充分不必要条件，等价于q是p的充分不必要条件．故a≥1.‎ ‎2．已知“命题p(x－m)2＞3(x－m)”是“命题qx2＋3x－4＜‎0”‎成立的必要不充分条件，则实数m的取值范围为________________．‎ 解析命题px＞m＋3或x＜m，‎ 命题q－4＜x＜1.‎ 因为p是q成立的必要不充分条件，‎ 所以m＋3≤－4或m≥1，‎ 故m≤－7或m≥1.‎ 答案(－∞，－7]∪[1，＋∞)‎ 一抓基础，多练小题做到眼疾手快 ‎1．“(2x－1)x＝‎0”‎是“x＝‎0”‎的(　　)‎ A．充分不必要条件　　　 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 解析选B　若(2x－1)x＝0，则x＝或x＝0，即不一定是x＝0；若x＝0，则一定能推出(2x－1)x＝0.故“(2x－1)x＝‎0”‎是“x＝0”的必要不充分条件．‎ ‎2．已知集合A＝{1，m2＋1}，B＝{2,4}，则“m＝”是“A∩B＝{4}”的(　　)‎ A．充分不必要条件　　　 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 解析选A　若A∩B＝{4}，则m2＋1＝4，∴m＝±，故“m＝”是“A∩B＝{4}”的充分不必要条件．‎ ‎3．(2017·山东重点中学模拟)已知命题p“正数a的平方不等于‎0”‎，命题q“若a不是正数，则它的平方等于‎0”‎，则q是p的(　　)‎ A．逆命题 B．否命题 C．逆否命题 D．否定 解析选B　命题p“正数a的平方不等于‎0”‎写成“若a是正数，则它的平方不等于‎0”‎，从而q是p的否命题．‎ ‎4．命题p“若x2<1，则x<‎1”‎的逆命题为q，则p与q的真假性为(　　)‎ A．p真q真 B．p真q假 C．p假q真 D．p假q假 解析选B　q若x<1，则x2<1.‎ ‎∵px2<1，则－15是x>a的充分条件，则实数a的取值范围为(　　)‎ A．a>5 B．a≥5‎ C．a<5 D．a≤5‎ 解析选D　由x>5是x>a的充分条件知，{x|x>5}⊆{x|x>a}．‎ ‎∴a≤5，故选D.‎ 二保高考，全练题型做到高考达标 ‎1．命题“若一个数是负数，则它的平方是正数”的逆命题是(　　)‎ A．“若一个数是负数，则它的平方不是正数”‎ B．“若一个数的平方是正数，则它是负数”‎ C．“若一个数不是负数，则它的平方不是正数”‎ D．“若一个数的平方不是正数，则它不是负数”‎ 解析选B　依题意得，原命题的逆命题是“若一个数的平方是正数，则它是负数”．‎ ‎2．(2016·四川高考)设p实数x，y满足x＞1且y＞1，q实数x，y满足x＋y＞2，则p是q的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 解析选A　∵∴x＋y＞2，即p⇒q.‎ 而当x＝0，y＝3时，有x＋y＝3＞2，但不满足x＞1且y＞1，即q⇒/ p．故p是q的充分不必要条件．‎ ‎3．有下列命题 ‎①“若x＋y>0，则x>0且y>‎0”‎的否命题；‎ ‎②“矩形的对角线相等”的否命题；‎ ‎③“若m≥1，则mx2－2(m＋1)x＋m＋3>0的解集是R”的逆命题；‎ ‎④“若a＋7是无理数，则a是无理数”的逆否命题．‎ 其中正确的是(　　)‎ A．①②③ B．②③④‎ C．①③④ D．①④‎ 解析选C　①的逆命题为“若x>0且y>0，则x＋y>‎0”‎为真，故否命题为真；‎ ‎②的否命题为“不是矩形的图形对角线不相等”，为假命题；‎ ‎③的逆命题为，若mx2－2(m＋1)x＋m＋3>0的解集为R，则m≥1.‎ ‎∵当m＝0时，解集不是R，‎ ‎∴应有 即m>1.∴③是真命题；‎ ‎④原命题为真，逆否命题也为真．‎ ‎4．如果x，y是实数，那么“x≠y”是“cos x≠cos y”的(　　)‎ A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分也不必要条件 解析选C　设集合A＝{(x，y)|x≠y}，B＝{(x，y)|cos x≠cos y}，则A的补集C＝{(x，y)|x＝y}，B的补集D＝{(x，y)|cos x＝cos y}，显然CD，所以BA.于是“x≠y”是“cos x≠cos y”的必要不充分条件．‎ ‎5．命题“对任意x∈[1,2)，x2－a≤‎0”‎为真命题的一个充分不必要条件可以是(　　)‎ A．a≥4 B．a>4‎ C．a≥1 D．a>1‎ 解析选B　要使“对任意x∈[1,2)，x2－a≤‎0”‎为真命题，只需要a≥4，∴a>4是命题为真的充分不必要条件．‎ ‎6．命题“若a>b，则ac2>bc2(a，b∈R)，”否命题的真假性为________．‎ 解析命题的否命题为“若a≤b，则ac2≤bc‎2”‎．若c＝0，结论成立．若c≠0，不等式ac2≤bc2也成立．故否命题为真命题．‎ 答案真 ‎7．在命题“若m＞－n，则m2＞n‎2”‎的逆命题、否命题、逆否命题中，假命题的个数是________．‎ 解析若m＝2，n＝3，则2>－3，但22<32，所以原命题为假命题，则逆否命题也为假命题，若m＝－3，n＝－2，则(－3)2>(－2)2，但－3<2，所以逆命题是假命题，则否命题也是假命题．故假命题的个数为3.‎ 答案3‎ ‎8．下列命题 ‎①“a>b”是“a2>b‎2”‎的必要条件；②“|a|>|b|”是“a2>b‎2”‎的充要条件；③“a>b”是“a＋c>b＋c”的充要条件．‎ 其中是真命题的是________(填序号)．‎ 解析①a>b⇒/ a2>b2，且a2>b2⇒/ a>b，故①不正确；‎ ‎②a2>b2⇔|a|>|b|，故②正确；‎ ‎③a>b⇒a＋c>b＋c，且a＋c>b＋c⇒a>b，故③正确．‎ 答案②③‎ ‎9．设等比数列{an}的公比为q，前n项和为Sn，则“|q|＝‎1”‎是“S4＝2S‎2”‎的________条件．‎ 解析∵等比数列{an}的前n项和为Sn，又S4＝2S2，‎ ‎∴a1＋a2＋a3＋a4＝2(a1＋a2)，∴a3＋a4＝a1＋a2，‎ ‎∴q2＝1⇔|q|＝1，∴“|q|＝‎1”‎是“S4＝2S‎2”‎的充要条件．‎ 答案充要 ‎10．已知集合A＝，B＝{x|x＋m2≥1}．若“x∈A”是“x∈B”的充分条件，求实数m的取值范围．‎ 解y＝x2－x＋1＝2＋，‎ ‎∵x∈，∴≤y≤2，‎ ‎∴A＝.‎ 由x＋m2≥1，得x≥1－m2，‎ ‎∴B＝{x|x≥1－m2}．‎ ‎∵“x∈A”是“x∈B”的充分条件，‎ ‎∴A⊆B，∴1－m2≤，‎ 解得m≥或m≤－，‎ 故实数m的取值范围是∪.‎ 三上台阶，自主选做志在冲刺名校 ‎1．设{an}是公比为q的等比数列，则“q>‎1”‎是“{an}为递增数列”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 解析选D　当等比数列{an}的首项a1<0，公比q>1时，如an＝－2n是递减数列，所以充分性不成立；‎ 反之，若等比数列{an}为递增数列，‎ 则或所以必要性不成立，即“q>1”是“{an}为递增数列”的既不充分也不必要条件．‎ ‎2．已知αx≥a，β|x－1|<1.若α是β的必要不充分条件，则实数a的取值范围为________．‎ 解析αx≥a，可看作集合A＝{x|x≥a}，‎ ‎∵β|x－1|<1，∴00时，B＝{x|a0时，B＝{x|a0；q“x>‎1”‎是“x>‎2”‎的充分不必要条件．则下列命题为真命题的是(　　)‎ A．p∧q　　　　　　　　 B．綈p∧綈q C．綈p∧q D．p∧綈q 解析选D　因为指数函数的值域为(0，＋∞)，所以对任意x∈R，y＝2x>0恒成立，故p为真命题；因为当x>1时，x>2不一定成立，反之当x>2时，一定有x>1成立，故“x>1”是“x>2”的必要不充分条件，故q为假命题，则p∧q，綈p为假命题，綈q为真命题，綈p∧綈q，綈p∧q为假命题，p∧綈q为真命题．‎ ‎2．命题p∃x0∈R，x－x0＋1≤0的否定是(　　)‎ A．∃x0∈R，x－x0＋1>0 B．∀x∈R，x2－x＋1≤0‎ C．∀x∈R，x2－x＋1>0 D．∃x0∈R，x－x0＋1<0‎ 答案C ‎3．已知命题px2＋4x＋3≥0，qx∈Z，且“p∧q”与“綈q”同时为假命题，则x＝________.‎ 解析若p为真，则x≥－1或x≤－3，‎ 因为“綈q”为假，则q为真，即x∈Z，‎ 又因为“p∧q”为假，‎ 所以p为假，‎ 故－3sin x B．∃x0∈R，sin x0＋cos x0＝2‎ C．∀x∈R,3x>0 D．∃x0∈R，lg x0＝0‎ 解析选B　因为对∀x∈R，sin x＋cos x＝sin≤，所以“∃x0∈R，sin x0＋cos x0＝‎2”‎为假命题．‎ ‎2．设x∈Z，集合A是奇数集，集合B是偶数集．若命题p∀x∈A,2x∈B，则(　　)‎ A．綈p∀x∈A,2x∉B　　 B．綈p∀x∉A,2x∉B C．綈p∃x0∉A,2x0∈B D．綈p∃x0∈A,2x0∉B 解析选D　命题p∀x∈A,2x∈B是一个全称命题，其命题的否定綈p应为∃x0∈A,2x0∉B，故选D.‎ ‎3．(2017·西安质检)已知命题p∃x0∈R，log2(3x0＋1)≤0，则(　　)‎ A．p是假命题；綈p∀x∈R，log2(3x＋1)≤0‎ B．p是假命题；綈p∀x∈R，log2(3x＋1)>0‎ C．p是真命题；綈p∀x∈R，log2(3x＋1)≤0‎ D．p是真命题；綈p∀x∈R，log2(3x＋1)>0‎ 解析选B　∵3x>0，∴3x＋1>1，则log2(3x＋1)>0，∴p是假命题綈p∀x∈R，log2(3x＋1)>0.故应选B.‎ ‎[谨记通法]‎ ‎1．全称命题与特称命题的否定 ‎(1)改写量词确定命题所含量词的类型，省去量词的要结合命题的含义加上量词，再对量词进行改写．‎ ‎(2)否定结论对原命题的结论进行否定．‎ ‎2．全称命题与特称命题真假的判断方法 不管是全称命题，还是特称命题，若其真假不容易正面判断时，可先判断其否定的真假.‎ 命题名称 真假 判断方法一 判断方法二 全称命题 真 所有对象使命题真 否定为假 假 存在一个对象使命题假 否定为真 特称命题 真 存在一个对象使命题真 否定为假 假 所有对象使命题假 否定为真 ‎[典例引领]‎ ‎(2017·海口调研)已知命题p若a0，使得x0－1－ln x0＝0，则下列命题为真命题的是(　　)‎ A．p∧q　　　　　　　 B．p∨(綈q)‎ C．(綈p)∧q D．(綈p)∧(綈q)‎ 解析选C　依题意，对于p，注意到当c＝0时，ac2＝bc2，因此命题p是假命题；对于q，注意到当x0＝1时，x0－1－ln x0＝0，因此命题q是真命题，命题綈q是假命题，p∧q是假命题，p∨(綈q)是假命题，(綈p)∧q是真命题，(綈p)∧(綈q)是假命题，综上所述，选C.‎ ‎[由题悟法]‎ 判断含有逻辑联结词命题真假的2个步骤 ‎(1)先判断简单命题p，q的真假．‎ ‎(2)再根据真值表判断含有逻辑联结词命题的真假．‎ ‎[即时应用]‎ ‎1．已知命题p∀x∈R,2x<3x，命题q∃x∈R，x2＝2－x，若命题(綈p)∧q为真命题，则x的值为(　　)‎ A．1　　　 B．－‎1　‎　　　‎ C．2　　　　 D．－2‎ 解析选D　∵綈p∃x∈R,2x≥3x，要使(綈p)∧q为真，‎ ‎∴綈p与q同时为真．由2x≥3x得x≥1，∴x≤0，‎ 由x2＝2－x得x2＋x－2＝0，‎ ‎∴x＝1或x＝－2，又x≤0，∴x＝－2.‎ ‎2．已知命题p若x>y，则－x<－y；命题q若x>y，则x2>y2.在命题①p∧q；②p∨q；③p∧(綈q)；④(綈p)∨q中，真命题是(　　)‎ A．①③ B．①④ C．②③ D．②④‎ 解析选C　由不等式的性质可知，命题p是真命题，命题q为假命题，故①p∧q为假命题；②p∨q为真命题；③綈q为真命题，则p∧(綈q)为真命题；④綈p为假命题，则(綈p)∨q为假命题，故选C.‎ ‎[典例引领]‎ 给定命题p对任意实数x都有ax2＋ax＋1>0成立；q关于x的方程x2－x＋a＝0有实数根．如果p∨q为真命题，p∧q为假命题，求实数a的取值范围．‎ 解当p为真命题时，“对任意实数x都有ax2＋ax＋1>0成立”⇔a＝0或∴0≤a<4.‎ 当q为真命题时，“关于x的方程x2－x＋a＝0有实数根”⇔Δ＝1－‎4a≥0，∴a≤.‎ ‎∵p∨q为真命题，p∧q为假命题，‎ ‎∴p，q一真一假．‎ ‎∴若p真q假，则0≤a<4，且a>，∴0，若p∨q为假命题，则实数m的取值范围是(　　)‎ A．[2，＋∞)　　　　　　　 B．(－∞，－2]‎ C．(－∞，－2]∪[2，＋∞) D．[－2,2]‎ 解析选A　依题意知，p，q均为假命题．当p是假命题时，mx2＋1>0恒成立，则有m≥0；当q是假命题时，则有Δ＝m2－4≥0，m≤－2或m≥2.因此由p，q均为假命题得即m≥2.‎ ‎2．已知函数f(x)＝x2＋mx＋1，若命题“∃x0>0，f(x0)<‎0”‎为真，则m的取值范围是________．‎ 解析因为函数f(x)＝x2＋mx＋1的图象过点(0,1)，若命题“∃x0>0，f(x0)<‎0”‎为真，则函数f(x)＝x2＋mx＋1的图象的对称轴必在y轴的右侧，且与x轴有两个不同交点，所以解得m<－2，所以m的取值范围是(－∞，－2)．‎ 答案(－∞，－2)‎ 一抓基础，多练小题做到眼疾手快 ‎1．命题“∃x0≤0，x≥‎0”‎的否定是(　　)‎ A．∀x≤0，x2<0　　　　 B．∀x≤0，x2≥0‎ C．∃x0>0，x>0 D．∃x0<0，x≤0‎ 答案A ‎2．已知命题p对任意x∈R，总有|x|≥0；‎ qx＝1是方程x＋2＝0的根．‎ 则下列命题为真命题的是(　　)‎ A．p∧綈q B．綈p∧q C．綈p∧綈q D．p∧q 解析选A　由题意知命题p是真命题，命题q是假命题，故綈p是假命题，綈q 是真命题，由含有逻辑联结词的命题的真值表可知p∧綈q是真命题．‎ ‎3．已知命题p“x>‎3”‎是“x2>‎9”‎的充要条件，命题q“a2>b‎2”‎是“a>b”的充要条件，则(　　)‎ A．p∨q为真 B．p∧q为真 C．p真q假 D．p∨q为假 解析选D　由x>3能够得出x2>9，反之不成立，故命题p是假命题；由a2>b2可得|a|>|b|，但a不一定大于b，反之也不一定成立，故命题q是假命题．所以p∨q为假．‎ ‎4．(2017·唐山一模)已知命题p∃x0∈N，x0，即a2－‎2a－3>0，解得a<－1或a>3，故选D.‎ 二保高考，全练题型做到高考达标 ‎1．命题“∀n∈N*，f(n)∈N*且f(n)≤n”的否定形式是(　　)‎ A．∀n∈N*，f(n)∉N*且f(n)>n B．∀n∈N*，f(n)∉N*或f(n)>n C．∃n0∈N*，f(n0)∉N*且f(n0)>n0‎ D．∃n0∈N*，f(n0)∉N*或f(n0)>n0‎ 解析选D　全称命题的否定为特称命题，因此命题“∀n∈N*，f(n)∈N*且f(n)≤n”的否定形式是“∃n0∈N*，f(n0)∉N*或f(n0)>n‎0”‎，故选D.‎ ‎2．(2016·衡阳一模)已知命题p∃α∈R，cos(π－α)＝cos α；命题q∀x∈R，x2＋1>0.则下面结论正确的是(　　)‎ A．p∧q是真命题 B．p∧q是假命题 C．綈p是真命题 D．p是假命题 解析选A　对于p取α＝，则cos(π－α)＝cos α，正确；‎ 对于命题q∀x∈R，x2＋1>0，正确．由此可得p∧q是真命题．故选A.‎ ‎3．(2017·皖南八校联考)下列命题中，真命题是(　　)‎ A．存在x0∈R，sin2＋cos2＝ B．任意x∈(0，π)，sin x>cos x C．任意x∈(0，＋∞)，x2＋1>x D．存在x0∈R，x＋x0＝－1‎ 解析选C　对于A选项∀x∈R，sin2＋cos2＝1，故A为假命题；对于B选项存在x＝，sin x＝，cos x＝，sin x0恒成立，C为真命题；对于D选项x2＋x＋1＝2＋>0恒成立，不存在x0∈R，使x＋x0＝－1成立，故D为假命题．‎ ‎4．已知命题p∀x>0，x＋≥4；命题q∃x0∈(0，＋∞)，2x0＝.则下列判断正确的是(　　)‎ A．p是假命题 B．q是真命题 C．p∧(綈q)是真命题 D．(綈p)∧q是真命题 解析选C　因为当x>0时，x＋≥2 ＝4，当且仅当x＝2时等号成立，所以p是真命题，当x>0时，2x>1，所以q是假命题，‎ 所以p∧(綈q)是真命题，(綈p)∧q是假命题．‎ ‎5．(2017·南昌模拟)下列说法错误的是(　　)‎ A．命题“若x2－5x＋6＝0，则x＝‎2”‎的逆否命题是“若x≠2，则x2－5x＋6≠‎‎0”‎ B．若命题p存在x0∈R，x＋x0＋1<0，则綈p对任意x∈R，x2＋x＋1≥0‎ C．若x，y∈R，则“x＝y”是“xy≥‎2”‎的充要条件 D．已知命题p和q，若“p或q”为假命题，则命题p与q中必一真一假 解析选D　由原命题与逆否命题的关系知A正确；由特称命题的否定知B正确；由xy≥2⇔4xy≥(x＋y)2⇔4xy≥x2＋y2＋2xy⇔(x－y)2≤0⇔x＝y知C正确；对于D，命题“p或q”为假命题，则命题p与q均为假命题，所以D不正确．‎ ‎6．命题p的否定是“对所有正数x，＞x＋‎1”‎，则命题p可写为________________________．‎ 解析因为p是綈p的否定，所以只需将全称命题变为特称命题，再对结论否定即可．‎ 答案∃x0∈(0，＋∞)，≤x0＋1‎ ‎7．(2017·枣庄一模)若“∀x∈，m≤tan x＋‎1”‎为真命题，则实数m的最大值为________．‎ 解析“∀x∈，m≤tan x＋‎1”‎为真命题，可得－1≤tan x≤1，∴0≤tan x＋1≤2，∴实数m的最大值为0.‎ 答案0‎ ‎8．已知命题“∀x∈R，x2－5x＋a>‎0”‎的否定为假命题，则实数a的取值范围是________．‎ 解析由“∀x∈R，x2－5x＋a>‎0”‎的否定为假命题，可知原命题必为真命题，即不等式x2－5x＋a>0对任意实数x恒成立．‎ 设f(x)＝x2－5x＋a，则其图象恒在x轴的上方．故Δ＝25－4×a<0，‎ 解得a>，即实数a的取值范围为.‎ 答案 ‎9．下列结论 ‎①若命题p∃x0∈R，tan x0＝2；命题q∀x∈R，x2－x＋>0.则命题“p∧(綈q)”是假命题；‎ ‎②已知直线l1ax＋3y－1＝0，l2x＋by＋1＝0，则l1⊥l2的充要条件是＝－3；‎ ‎③“设a，b∈R，若ab≥2，则a2＋b2>‎4”‎的否命题为“设a，b∈R，若ab<2，则a2＋b2≤‎4”‎．‎ 其中正确结论的序号为________．(把你认为正确结论的序号都填上)‎ 解析在①中，命题p是真命题，命题q也是真命题，故“p∧(綈q)”是假命题是正确的．在②中，由l1⊥l2，得a＋3b＝0，所以②不正确．在③中“设a，b∈R，若ab≥2，则a2＋b2>‎4”‎的否命题为“设a，b∈R，若ab<2，则a2＋b2≤‎4”‎正确．‎ 答案①③‎ ‎10．已知命题p“存在a>0，使函数f(x)＝ax2－4x在(－∞，2]上单调递减”，命题q“存在a∈R，使∀x∈R,16x2－16(a－1)x＋1≠‎0”‎．若命题“p∧q”为真命题，求实数a的取值范围．‎ 解若p为真，则对称轴x＝－＝在区间(－∞，2]的右侧，即≥2，∴00)，q实数x满足20，∴A＝(a,‎4a)，‎ 又B＝(2,5]，则a≤2且‎4a>5，解得0}，则S∩T＝(　　)‎ A．[2,3] B．(－∞，2]∪[3，＋∞)‎ C．[3，＋∞) D．(0,2]∪[3，＋∞)‎ 解析选D　由题意知S＝{x|x≤2或x≥3}，则S∩T＝{x|00，则方程x2＋x－m＝0有实根”的逆否命题是(　　)‎ A．若方程x2＋x－m＝0有实根，则m>0‎ B．若方程x2＋x－m＝0有实根，则m≤0‎ C．若方程x2＋x－m＝0没有实根，则m>0‎ D．若方程x2＋x－m＝0没有实根，则m≤0‎ 解析选D　根据逆否命题的定义，命题“若m>0，则方程x2＋x－m＝0有实根”的逆否命题是“若方程x2＋x－m＝0没有实根，则m≤‎0”‎．‎ 命题点四　含有逻辑联结词的命题 命题指数☆☆☆‎ 难度中、低 ‎ 题型选择题 ‎1.(2014·辽宁高考)设a，b，c是非零向量，已知命题p若a·b＝0，b·c＝0，则a·c＝0；命题q若a∥b，b∥c，则a∥c.则下列命题中真命题是(　　)‎ A．p∨q B．p∧q C．(綈p)∧(綈q) D．p∨(綈q)‎ 解析选A　‎ 如图，若a＝A‎1A―→，b＝AB―→，c＝B1B―→，则a·c≠0，命题p为假命题；显然命题q为真命题，所以p∨q为真命题．‎ ‎2．(2013·湖北高考)在一次跳伞训练中，甲、乙两位学员各跳一次．设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为(　　)‎ A．(綈p)∨(綈q) B．p∨(綈q)‎ C．(綈p)∧(綈q) D．p∨q 解析选A　綈p甲没有降落在指定范围；綈q乙没有降落在指定范围，‎ 至少有一位学员没有降落在指定范围，即綈p或綈q发生．即为(綈p)∨(綈q)．‎ 命题点五　全称量词和存在量词 命题指数☆☆☆‎ 难度低 ‎ 题型选择题、填空题 ‎1.(2015·全国卷Ⅰ)设命题p∃n∈N，n2>2n，则綈p为(　　)‎ A．∀n∈N，n2>2n B．∃n∈N，n2≤2n C．∀n∈N，n2≤2n D．∃n∈N，n2＝2n 解析选C　因为“∃x∈M，p(x)”的否定是“∀x∈M，綈p(x)”，所以命题“∃n∈N，n2>2n”的否定是“∀n∈N，n2≤2n”．‎ ‎2．(2016·浙江高考)命题“∀x∈R，∃n∈N*，使得n≥x‎2”‎的否定形式是(　　)‎ A．∀x∈R，∃n∈N*，使得n＜x2‎ B．∀x∈R，∀n∈N*，使得n＜x2‎ C．∃x∈R，∃n∈N*，使得n＜x2‎ D．∃x∈R，∀n∈N*，使得n＜x2‎ 解析选D　由于特称命题的否定形式是全称命题，全称命题的否定形式是特称命题，所以“∀x∈R，∃n∈N*，使得n≥x‎2”‎的否定形式为“∃x∈R，∀n∈N*，使得n＜x‎2”‎．‎ ‎3．(2015·山东高考)若“∀x∈，tan x≤m”是真命题，则实数m的最小值为________．‎ 解析由题意，原命题等价于tan x≤m在区间上恒成立，即y＝tan x在上的最大值小于或等于m，又y＝tan x在上的最大值为1，所以m≥1，即m的最小值为1.‎ 答案1‎