2020-2021学年高一数学单元知识梳理：指数函数与对数函数 10页

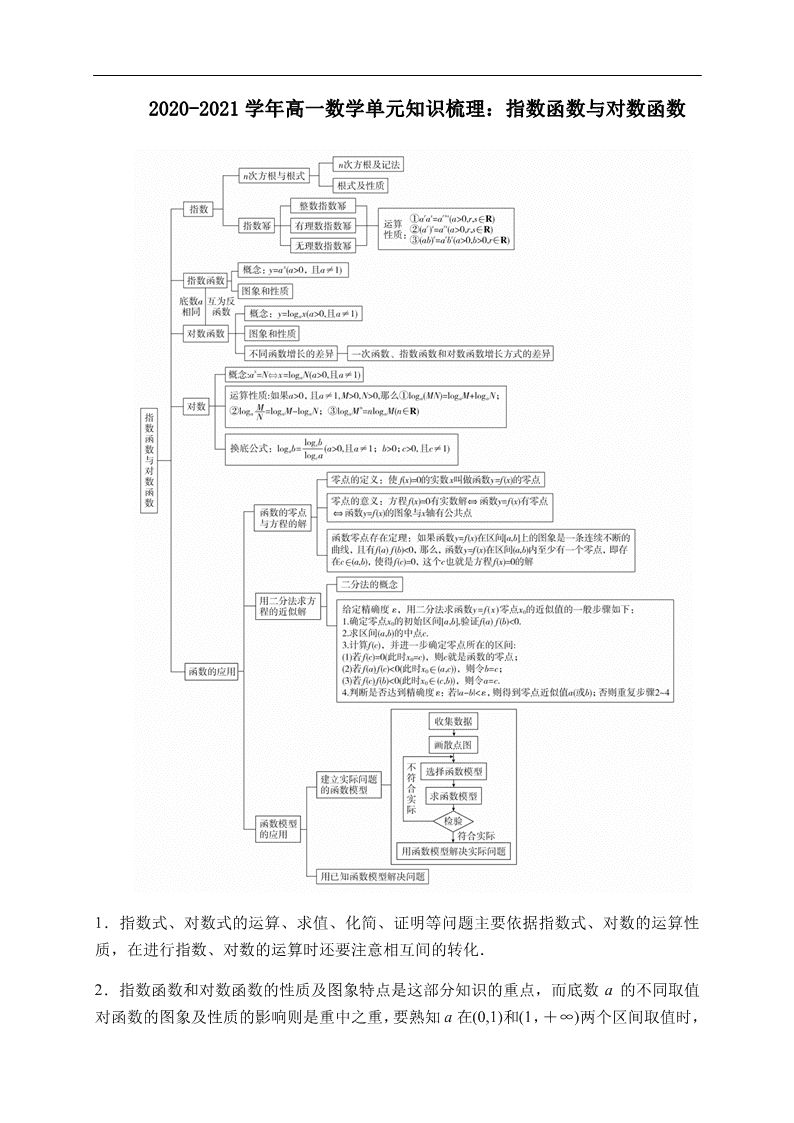
2020-2021 学年高一数学单元知识梳理：指数函数与对数函数 1．指数式、对数式的运算、求值、化简、证明等问题主要依据指数式、对数的运算性 质，在进行指数、对数的运算时还要注意相互间的转化． 2．指数函数和对数函数的性质及图象特点是这部分知识的重点，而底数 a 的不同取值 对函数的图象及性质的影响则是重中之重，要熟知 a 在(0,1)和(1，＋ ∞)两个区间取值时， 函数的单调性及图象特点． 3．比较几个数的大小是指数函数、对数函数性质的应用，在具体比较时，可以首先将 它们与零比较，分出正数、负数；再将正数与 1 比较，分出大于 1 还是小于 1；然后在 各类中两两相比较． 4．求含有指数函数和对数函数的复合函数的最值或单调区间时，首先要考虑指数函数、 对数函数的定义域，再由复合函数的单调性来确定其单调区间，要注意单调区间是函数 定义域的子集．其次要结合函数的图象，观察确定其最值或单调区间． 5．函数图象是高考考查的重点内容，在历年高考中都有涉及．考查形式有知式选图、 知图选式、图象变换以及用图象解题．函数图象形象地显示了函数的性质．在解方程或 不等式时，特别是非常规的方程或不等式，画出图象，利用数形结合能快速解决问题． 6．方程的解与函数的零点：方程 f(x)＝0 有实数解⇔函数 y＝f(x)有零点⇔函数 y＝f(x) 的图象与 x 轴有交点． 7．零点判断法：如果函数 y＝f(x)在区间[a，b]上的图象是一条连续不断的曲线，且有 f(a)f(b)<0，那么，函数 y＝f(x)在区间(a，b)内至少有一个零点，即存在 c∈(a，b)，使得 f(c)＝0，这个 c 也就是方程 f(x)＝0 的解． 注意：由 f(a)f(b)<0 可判定在(a，b)内至少有一个变号零点 c，除此之外，还可能有其他 的变号零点或不变号零点．若 f(a)f(b)>0，则 f(x)在(a，b)内可能有零点，也可能无零点． 8．二分法只能求出其中某一个零点的近似值，另外应注意初始区间的选择． 9．用函数建立数学模型解决实际问题的基本过程如下： 一、指数、对数函数的典型问题及求解策略 指数函数、对数函数的性质主要是指函数的定义域、值域、单调性等，其中单调性是高 考考查的重点，并且经常以复合函数的形式考查，求解此类问题时，要以已学函数的单 调性为主，结合复合函数单调性的判断法则，在函数定义域内进行讨论． 1．求定义域 【典例 1】1．（ 2020·河南高三其模拟）函数 2 34 ln xxy x  的定义域是（ ） A．（0，1）∪（1，4] B．（0，4] C．（0，1） D．（0，1）∪[4，+∞） 【答案】A 【解析】 22 34034 ln ln0,0 xxxxy x xx   14 (0,1)(1,4]0,1 x xxx   故选：A 2．（ 2020·湖南天心长郡中学高一月考）函数 2()2logfxxx  的定义域是（ ） A． (0,2] B．[0,2) C． [0 ,2] D．(0,2) 【答案】A 【解析】由题意可得， 0 20 x x    , 解得 02x.故选：A. 2．比较大小问题 比较几个数的大小是指数、对数函数的又一重要应用，其基本方法是：将两个需要比较 大小的实数看成某类函数的函数值，然后利用该类函数的单调性进行比较；有时也采用 搭桥法、图象法、特殊值法、作图法等方法． 【典例 2】若 0logy3，错误． 对于 C，函数 y＝log4x 在(0，＋∞)上单调递增，故 log4x y，错误． 【典例 3】比较三个数 0.32，log20.3,20.3 的大小． 【解析】解法一：∵0<0.32<12＝1，log20.320＝1，∴log20.3<0.32<20.3. 解法二：作出函数 y＝x2，y＝log2x，y＝2x 的大致图象，如图所示，画出直线 x＝0.3， 根据直线与三个函数图象的交点位置，即可看出 log20.3<0.32<20.3. 3．与指数、对数函数相关的单调性问题 【典例 4】是否存在实数 a，使函数 f（x）＝loga（ax2﹣x）在区间[2，4]上是增函数？若存在，求 出 a 的取值范围；若不存在，说明理由． 【解析】设 u（x）＝ax2﹣x，显然二次函数 u 的对称轴为 x= 1 2푎． ①当 a＞1 时，要使函数 f（x）在[2，4]上为增函数，则 u（x）＝ax2﹣x 在[2，4]上为增函数， 故应有 { 1 2푎 ≤ 2 푢(2) = 4푎 − 2＞0 ，解得 a＞ 1 2．综合可得，a＞1． ②当 0＜a＜1 时，要使函数 f（x）在[2，4]上为增函数， 则 u（x）＝ax2﹣x 在[2，4]上为减函数， 应有 { 1 2푎 ≥ 4 푢(4) = 16푎 − 4＞0 ，解得 a∈∅． 综上，a＞1 时，函数 f（x）＝loga（ax2﹣x）在区间[2，4]上为增函数． 二、函数的图象问题 对于给定的函数图象，要能从函数左右、上下的分布范围、变化趋势、对称性等方面研 究函数的定义域、值域、单调性、奇偶性、周期性等性质．注意图象与函数解析式中参 数的关系，能够通过变换画出函数的图象． 1．图象的变换 【典例 5】为了得到函数 y＝lg 10 3x 的图象，只需把函数 y＝lg x 的图象上所有的点( ) A．向左平移 3 个单位长度，再向上平移 1 个单位长度 B．向右平移 3 个单位长度，再向上平移 1 个单位长度 C．向左平移 3 个单位长度，再向下平移 1 个单位长度 D．向右平移 3 个单位长度，再向下平移 1 个单位长度 【答案】C 【解析】∵y＝lg ＝lg (x＋3)－1，∴只需将 y＝lg x 的图象上所有的点向左平移 3 个单位长度，再向下平移 1 个单位长度，即可得到函数 y＝lg 的图象． 2．根据函数解析式确定图象 【典例 6】已知 f(x)＝ax－2，g(x)＝loga|x|(a>0，且 a≠1)，若 f(4)g(4)<0，则 y＝f(x)，y＝ g(x)在同一平面直角坐标系内的大致图象是( ) 【答案】B 【解析】由 f(4)g(4)<0 知 a2·loga4<0，∴loga4<0，∴0