【数学】2020届一轮复习人教A版第67课平面的基本性质及线线、线面的位置关系学案（江苏专用） 7页

第67课　平面的基本性质及线线、线面之间的位置关系 ‎1. 了解4个公理及公理3的3个推论，等角定理，异面直线的判定定理.‎ ‎2. 理解空间点、线、面的位置关系，会用数学语言规范地表述空间点、线、面的位置关系；引导学生理解反证法，通过“反设”与“归谬”，进而得到正确的结论.‎ ‎1. 阅读：必修2第21～30页.‎ ‎2. 解悟：①4个公理及公理3的3个推论，等角定理的3种语言；②空间两直线的几种位置关系；③异面直线的判定定理.‎ ‎3. 践习：在教材空白处，完成第25页练习第7、8题；第30页练习第6、7题.‎ ‎　基础诊断　‎ ‎1. 已知点A、B，直线l，平面α、β，给出下列命题：①若A∈l，B∈l且A∈α，B∈α，则l⊂α；②若A∈α，A∈β，B∈α，B∈β，则α∩β＝AB；③若l⊄α，A∈l，则A∉α；④若A，B，C∈α，A，B，C∈β，且A，B，C三点不共线，则α与β重合；⑤梯形是平面图形；⑥四边形的两条对角线必相交于一点.其中正确的命题是　①②④⑤　.(填序号)‎ 解析：①由公理1可知，①正确；②因为A∈α，B∈α，所以AB⊂α，同理AB⊂β，所以α∩β＝AB，故②正确；③l⊄α分两种情况，l与α相交或l∥α，当l与α相交，A为交点时，A∈α，故③错误；④由于A，B，C三点不共线，所以A，B，C三点只能确定一个平面，所以α与β重合，故④正确；⑤因为梯形的上、下底平行，经过两条平行直线，有且只有一个平面，所以梯形是平面图形，故⑤正确；⑥空间四边形的两条对角线异面，不相交，故⑥错误，故填①②④⑤.‎ ‎2. 在正方体ABCDA1B1C1D1中，P，Q，R分别是AB，AD，B1C1的中点，那么正方体的过点P，Q，R的截面图形是　六边形　.‎ 解析：如图，作RG∥PQ交C1D1于点G，连结QP并延长与CB的延长线交于点M，连结MR交BB1于点E，连结PE.延长PQ交CD的延长线于点N，连结NG交DD1于点F，连结QF，所以截面为六边形PQFGRE.‎ ‎3. 两两平行的三条直线可确定　1或3　个平面.‎ 解析：若三条平行直线共面时，可确定1个平面；若三条直线，两两平行且不共面时，可确定3个平面，如三棱柱的三条侧棱，故可确定1或3个平面.‎ ‎4. 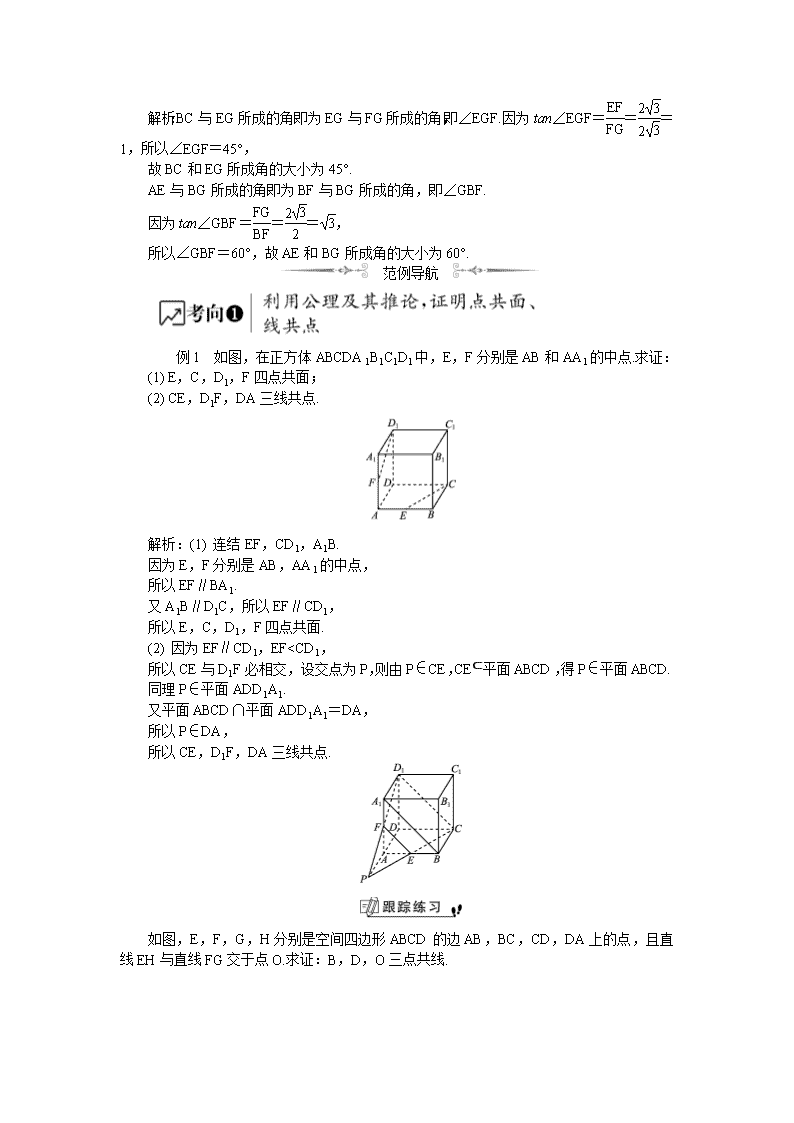如图所示，已知在长方体ABCDEFGH中，AB＝2，AD＝2，AE＝2，则BC和EG所成角的大小是　45°　，AE和BG所成角的大小是　60°　.‎ 解析：BC与EG所成的角即为EG与FG所成的角，即∠EGF.因为tan∠EGF＝＝＝1，所以∠EGF＝45°，‎ 故BC和EG所成角的大小为45°.‎ AE与BG所成的角即为BF与BG所成的角，即∠GBF.‎ 因为tan∠GBF＝＝＝，‎ 所以∠GBF＝60°，故AE和BG所成角的大小为60°.‎ ‎　范例导航　‎ ‎　　例1　如图，在正方体ABCDA1B1C1D1中，E，F分别是AB和AA1的中点.求证：‎ ‎(1) E，C，D1，F四点共面；‎ ‎(2) CE，D1F，DA三线共点.‎ 解析：(1) 连结EF，CD1，A1B.‎ 因为E，F分别是AB，AA1的中点，‎ 所以EF∥BA1.‎ 又A1B∥D1C，所以EF∥CD1，‎ 所以E，C，D1，F四点共面.‎ ‎(2) 因为EF∥CD1，EF