数学理卷·2018届西藏林芝地区二高高三上学期第一次月考（2017 8页

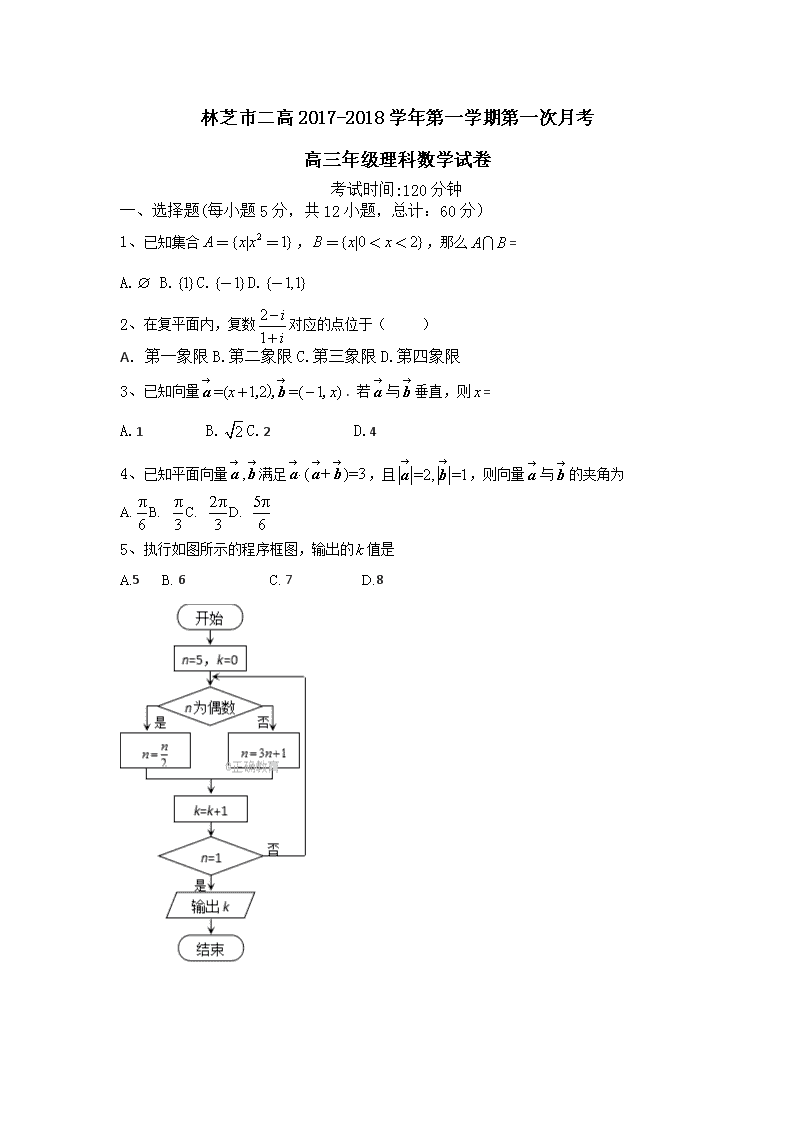
林芝市二高 2017-2018 学年第一学期第一次月考 高三年级理科数学试卷 考试时间:120 分钟 一、选择题(每小题 5 分，共 12 小题，总计：60 分） 1、已知集合 ， ，那么 = A. B. C. D. 2、在复平面内，复数 对应的点位于（　 　） A．第一象限 B.第二象限 C.第三象限 D.第四象限 3、已知向量 . 若 与 垂直，则 = A.1 B. C.2 D.4 4、已知平面向量 满足 ，且 ，则向量 与 的夹角为 A. B. C. D. 5、执行如图所示的程序框图，输出的 值是 A.5 B. 6 C. 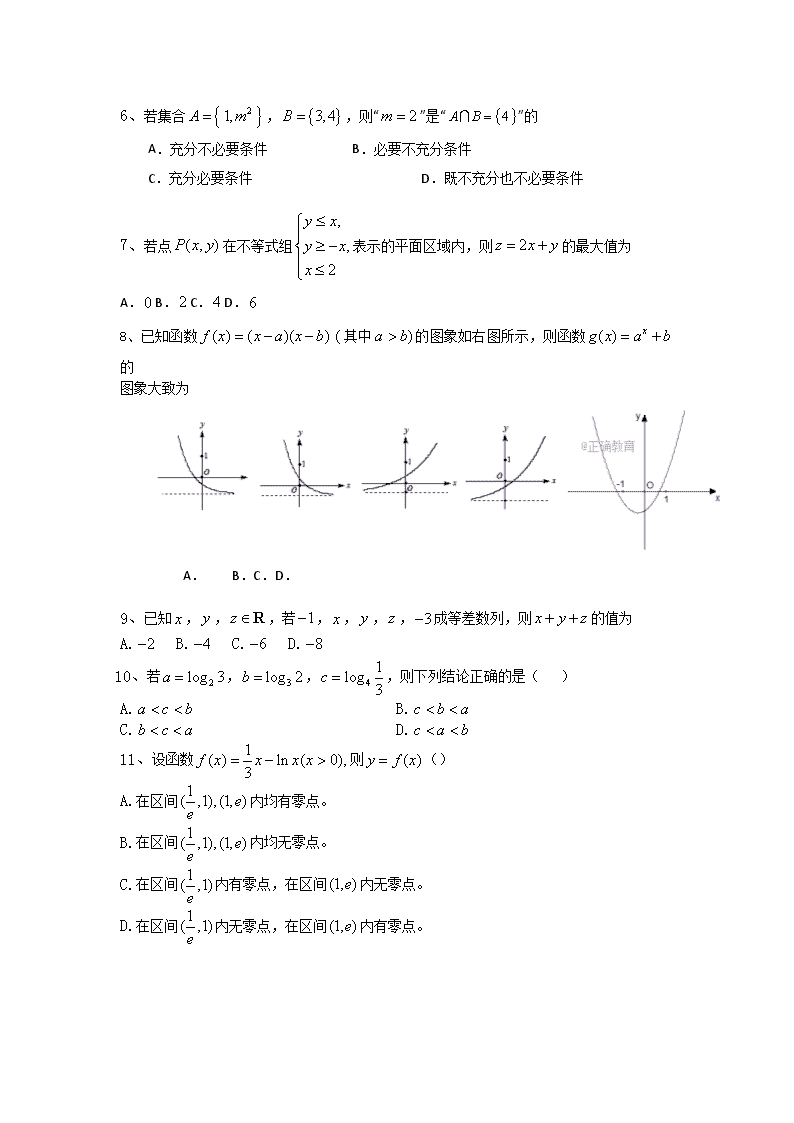7 D.8 2 2{ | 1}A x x= = { |0 2}B x x= < < A B Æ {1} { 1}- { 1,1}- 2 1 i i − + =( 1 2 =( 1 )x x → → + −, , ,a b) → a → b x , → → a b ( )=3 → → → ⋅a a+ b =2, =1 → → a b → a → b 6 π 3 π 3 2π 6 5π k 6、若集合 ， ，则“ ”是“ ”的 A．充分不必要条件 B．必要不充分条件 C．充分必要条件　　　　　　　　　　　　D．既不充分也不必要条件 7、若点 在不等式组 表示的平面区域内，则 的最大值为 A． B． C． D． 8、已知函数 其中 的图象如右图所示，则函数 的 图象大致为 A． B．C．D． 9、已知 ， ， ，若 ， ， ， ， 成等差数列，则 的值为 A. B. C. D. 10、若 ， ， ，则下列结论正确的是（ ） A. B. C. D. 11、设函数 则 （） A.在区间 内均有零点。 B.在区间 内均无零点。 C.在区间 内有零点，在区间 内无零点。 D.在区间 内无零点，在区间 内有零点。 { }21,A m= { }3,4B = 2m = { }4=BA ( , )P x y , , 2 y x y x x ≤  ≥ −  ≤ 2z x y= + 0 2 4 6 ( ) ( )( )f x x a x b= − − ( )a b> ( ) xg x a b= + x y z ∈R 1− x y z 3− x y z+ + 2− 4− 6− 8− 2log 3a = 3log 2b = 4 1log 3c = a c b< < c b a< < b c a< < c a b< < 1( ) ln ( 0),3f x x x x= − > ( )y f x= 1( ,1),(1, )ee 1( ,1),(1, )ee 1( ,1)e (1, )e 1( ,1)e (1, )e 12、已知函数 若 ，则实数 的取值范围是 （） A. B. C. D. 二、填空题（每小题 5 分，共 4 小题，总计：20 分） 13、命题“ ”的否定是 14、已知某几何体的三视图如图所示，则该几何体的体积为 15、已知向量 ， .若 ，则实数 . 16、已知函数 ， .若方程 恰有 4 个互异的实数根， 则实数 的取值范围为________ 三、解答题（共 6 小题，总计：70 分，17-21 题每题 12 分，22 题 10 分） 17、（本小题满分 12 分） 已知各项都为正数的数列 满足 ， . （Ⅰ）求 ；（Ⅱ）求 的通项公式. 18、（本小题满分 12 分） 某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出 的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量 与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最 高气温位于区间 ，需求量为300瓶；如果最高气温低于20，需求量为200瓶，为 了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分 布表： 最高气温 天数 2 16 36 25 7 4    <− ≥+= 0,4 0,4)( 2 2 xxx xxxxf 2(2 ) ( )f a f a− > a ( , 1) (2, )−∞ − ∪ +∞ ( 1,2)− ( 2,1)− ( , 2) (1, )−∞ − ∪ +∞ 0 0 0(0, ),tan sin2x x x π∃ ∈ > (1,2) → =a ( , 2)λ → = −b → → a b λ = ( ) 2 3f x x x= + x R∈ ( ) 1 0f x a x− − = a { }na 1 1a = 2 1 1(2 1) 2 0n n n na a a a+ +− − − = 2 3,a a { }na [20,25) [ )10 15， [ )15 20， [ )20 25， [ )25 30， [ )30 35， [ )35 40， 以最高气温位于各区间的频率代替最高气温位于该区间的概率． （1）求六月份这种酸奶一天的需求量 （单位：瓶）的分布列； （2）设六月份一天销售这种酸奶的利润为 （单位：元）．当六月份这种酸奶一天的 进货量（单位：瓶）为多少时， 的数学期望达到最大值？ 19、（本小题满分 12 分） 已知函数 . （Ⅰ）求 的最小正周期； （Ⅱ）若函数 的图象是由 的图象向右平移 个单位长度得到的，当 [ , ]时，求 的最大值和最小值. 20、（本小题满分 12 分） 已知函数 ，且 。 （Ⅰ）求 ； （Ⅱ）证明： 存在唯一的极大值点 ，且 . 21、（本小题满分 12 分） 已知椭圆 的长轴长为 ，点 （2，1）在椭圆上，平行于 （ 为坐标原点）的直线 交椭圆于 两点， 在 轴上的截距为 . （Ⅰ）求椭圆的方程； （Ⅱ）求 的取值范围； 22、（本小题满分 10 分） 在直角坐标系 xOy 中，圆 C 的方程为 . （Ⅰ）以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，求 C 的极坐标方程； （Ⅱ）直线 l 的参数方程是 （t 为参数），l 与 C 交于 A，B 两点， , 求 l 的斜率. 2 2( + 6) + = 25x y cos sin x t α, y t α, ì =ïïíï =ïî 10AB = X Y Y 2 2( ) (sin2 cos2 ) 2sin 2f x x x x= + − ( )f x ( )y g x= ( )y f x= 8 π x∈ 0 4 π ( )y g x= ( ) 2 lnf x ax ax x x= − − ( ) 0f x ≥ a ( )f x 0x ( )2 2 0 2e f x− −< < 12 2 2 2 =+ b y a x )0( >> ba 24 P OP O l BA, l y m m 2017-2018 学年第一学期第一次月考高三年级理科数学答案 一、选择题(每小题 5 分，共 12 小题，总计：60 分） 1、B 2、D 3、A 4、C 5、A 6、A 7、D 8、A 9、C 10、B 11、D 12、C 三、填空题（每小题 5 分，共 4 小题，总计：20 分） 13、 14、 15、-1 16、 四、解答题（共 6 小题，总计：70 分，17-21 题每题 12 分，22 题 10 分） 17、（Ⅰ）由题意得 . .........5 分 （Ⅱ）由 得 . 因为 的各项都为正数，所以 . 故 是首项为 ，公比为 的等比数列，因此 . ......12 分 18、（1）由题意知， 所有可能取值为200,300,500，由表格数据知 ， ， . 因此 的分布列为： 200 300 500 0.2 0.4 0.4 （2）由题意知，这种酸奶一天的需求量至多为500，至少为200，因此只需考虑200 500 当 时， 若最高气温不低于25，则 ； 若最高气温位于区间[20,25），则 ； 若最高气温低于20，则 因此 当 时， 若最高气温不低于20，则 ； (0, ),tan sin2x x x π∀ ∈ ≤ 3 2 ( ) ( )0,1 9,+∞ 4 1,2 1 32 == aa 02)12( 11 2 =−−− ++ nnnn aaaa )1()1(2 1 +=++ nnnn aaaa { }na 2 11 =+ n n a a { }na 1 2 1 12 1 −= nna X ( ) 2 16200 0.290P X += = = ( ) 36300 0.490P X = = = ( ) 25 7 4500 0.490P X + += = = X X P n≤ ≤ 300 500n≤ ≤ 6 4 2Y n n n= − = 6 300 2( 300) 4 1200 2Y n n n= × + − − = − 6 200 2( 200) 4 800 2Y n n n= × + − − = − 2 0.4 (1200 2 ) 0.4 (800 2 ) 0.2 640 0.4EY n n n n= × + − × + − × = − 200 300n≤ < 6 4 2Y n n n= − = 若最高气温低于20，则 因此 所以 时， 的数学期望达到最大值，最大值为520元。 19、因为 , ........6 分 所以函数 的最小正周期 . ........8 分 （Ⅱ）依题意, [ ] . ........10 分 因为 ，所以 . ........11 分 当 ，即 时， 取最大值 ； 当 ，即 时， 取最小值 .........12 分 20、（1） 的定义域为 设 ，则 等价于 因为 ， 故 ， 而 ， 得 若 ，则 当 时， 单调递减； 6 200 2( 200) 4 800 2Y n n n= × + − − = − 2 (0.4 0.4) (800 2 ) 0.2 160 1.2EY n n n= × + + − × = + 300n = Y 2 2( ) (sin 2 cos2 ) 2sin 2f x x x x= + − sin 4 cos4x x= + 2 sin(4 )4x π= + ( )f x 2 π ( )y g x= = 2 sin 4( )8x π− 4 π+ 2 sin(4 )4x π= − 0 4x π≤ ≤ 344 4 4x π π π− ≤ − ≤ 4 4 2x π π− = 3 16x π= ( )g x 2 4 4 4x π π− = − 0x = ( )g x 1− ( )f x (0, )+∞ ( ) lng x ax a x= − − ( ) ( ), ( ) 0f x xg x f x= ≥ ( ) 0g x ≥ (1) 0, ( ) 0g g x= ≥ (1) 0g′ = 1( ) , (1) 1g x a g ax ′ ′= − = − 1a = 1a = 1( ) 1g x x ′ = − 0 1x< < ( ) 0, ( )g x g x′ < 当 时， 单调递增 所以 是 的极小值点，故 综上， （2）由（1）知 设 ，则 当 时， ；当 时， . 所以 在 单调递减，在 单调递增. 又 ，所以 在 有唯一零点 ，在 有唯 一零点 1，且当 时， ；当 时， ；当 时， . 因为 ，所以 是 的唯一极大值点. 由 得 ，故 . 由 得 . 因为 是 在 的最大值点，由 得 . 所以 21、（I）由已知可知 …………………………………1 分 设椭圆方程为 ，将点 代入解得 …………………………3 分 ∴椭圆方程为 ………………………5 分 （II）∵直线 平行于 ，且在 轴上的截距为 ,又 （ ） …………………………………7 分 128 22 =+ yx mxyl +=∴ 2 1的方程为： 1x > ( ) 0, ( )g x g x′ > 1x = ( )g x ( ) (1) 0g x g≥ = 1a = 2( ) ln , ( ) 2 2 lnf x x x x x f x x x′= − − = − − ( ) 2 2 lnh x x x= − − 1( ) 2h x x ′ = − 1(0, )2x∈ ( ) 0h x′ < 1( , )2x∈ +∞ ( ) 0h x′ > ( )h x 1(0, )2 1( , )2 +∞ 2 1( ) 0, ( ) 0, (1) 02h e h h− > < = ( )h x 1(0, )2 0x 1[ , )2 +∞ 0(0, )x x∈ ( ) 0h x > 0( ,1)x x∈ ( ) 0h x < (1, )x∈ +∞ ( ) 0h x > ( ) ( )f x h x′ = 0x x= ( )f x 0( ) 0f x′ = 0 0ln 2( 1)x x= − 0 0 0( ) (1 )f x x x= − 0 (0,1)x ∈ 0 1( ) 4f x < 0x x= ( )f x (0,1) 1 1(0,1), ( ) 0e f e− −′∈ ≠ 1 2 0( ) ( )f x f e e− −> = 2 2 0( ) 2e f x− −< < 22=a 18 2 22 =+ b yx )1,2(P 22 =b l OP y m 2 1=opk 0≠m 由 ①………………………………8 分 ∵直线 与椭圆交于 A、B 两个不同点， 解得 ，且 ≠ . 所以 的取值范围是 . …………………………………12 分 22、（Ⅰ） ；（Ⅱ） . （I）利用 ， 可得 C 的极坐标方程；（II）先将直线 的参数方程化 为普通方程，再利用弦长公式可得 的斜率． 试题解析：（I）由 可得 的极坐标方程 （II）在（I）中建立的极坐标系中，直线 的极坐标方程为 由 所对应的极径分别为 将 的极坐标方程代入 的极坐标方程得 于是 由 得 ， 所以 的斜率为 或 . 0422 128 2 1 22 22 =−++∴       =+ += mmxx yx mxy l 2 22 ) 4(2 4) 0m m∴∆ = − − >（ 2 2m− < < m 0 m ( ) ( )2,00,2 − 2 12 cos 11 0ρ ρ θ+ + = 15 3 ± 2 2 2x yρ = + cosx ρ θ= l l cos , sinx yρ θ ρ θ= = C 2 12 cos 11 0.ρ ρ θ+ + = l ( )Rθ α ρ= ∈ ,A B 1 2, ,ρ ρ l C 2 12 cos 11 0.ρ ρ α+ + = 1 2 1 212cos , 11,ρ ρ α ρ ρ+ = − = 2 2 1 2 1 2 1 2| | | | ( ) 4 144cos 44,AB ρ ρ ρ ρ ρ ρ α= − = + − = − | | 10AB = 2 3 15cos ,tan8 3 α α= = ± l 15 3 15 3 −