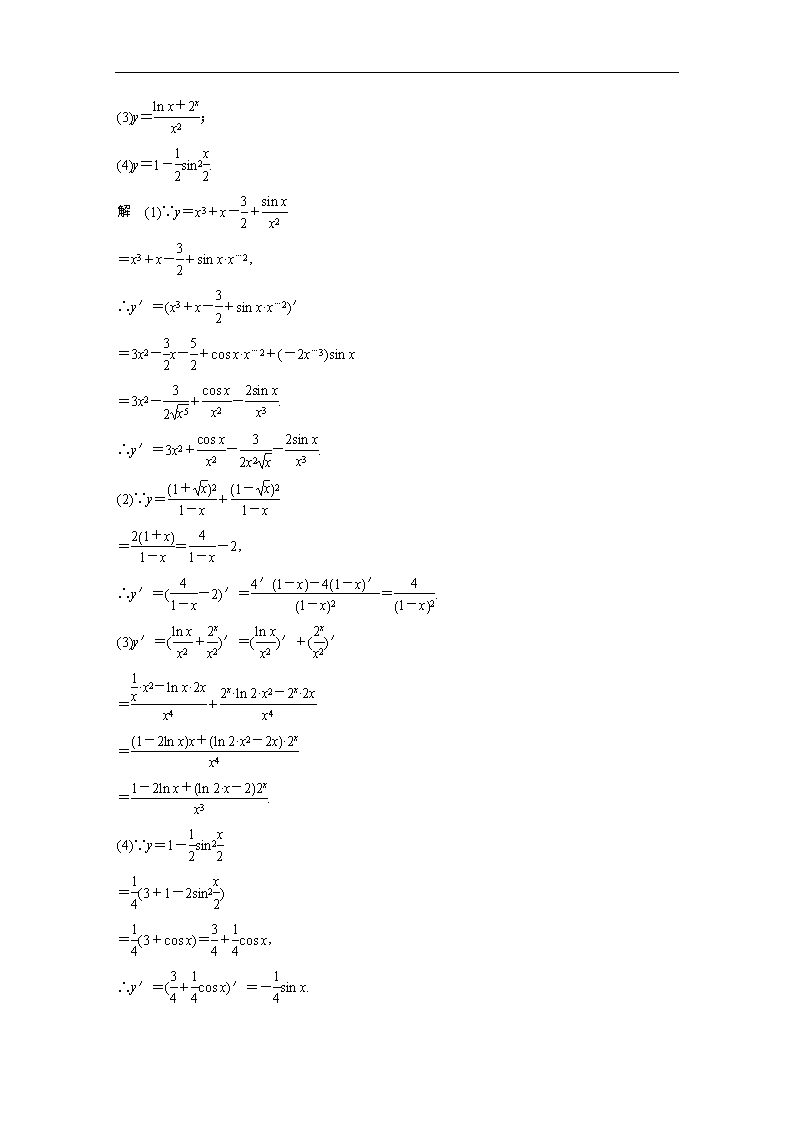高中数学选修2-2教案第二章 4_2 9页

‎4.2　导数的乘法与除法法则 明目标、知重点 ‎1．理解导数的乘法与除法法则．‎ ‎2．将导数公式和导数四则运算相结合，灵活解决一些导数问题．‎ 导数的乘法与除法法则 一般地，若两个函数f(x)和g(x)的导数分别是f′(x)和g′(x)，则[f(x)g(x)]′＝f′(x)g(x)＋f(x)g′(x)；‎ ′＝ (g(x)≠0)．‎ 特别地，当g(x)＝k时，有[kf(x)]′＝kf′(x)．‎ 探究点一　导数的运算法则 思考1　设函数y＝f(x)在x0处的导数为f′(x0)，g(x)＝x2，用导数定义求y＝f(x)g(x)＝x2f(x)在x0处的导数．‎ 答　经计算得：‎ y＝x2f(x)在x0处的导数为xf′(x0)＋2x0f(x0)．‎ 小结　一般地，若f(x)、g(x)的导数分别是f′(x)、g′(x)，‎ 则[f(x)g(x)]′＝f′(x)g(x)＋f(x)g′(x)，‎ ′＝(g(x)≠0)．‎ 思考2　应用导数公式和四则运算法则求导有哪些注意点？‎ 答　(1)要准确判断函数式的结构特点，选择合适的公式和法则；(2)求导前可以先对解析式适当化简变形，以利于求导．‎ 例1　求下列函数的导数：‎ ‎(1)y＝；‎ ‎(2)y＝＋；‎ ‎(3)y＝；‎ ‎(4)y＝1－sin2.‎ 解　(1)∵y＝x3＋x－＋ ‎＝x3＋x－＋sin x·x－2，‎ ‎∴y′＝(x3＋x－＋sin x·x－2)′‎ ‎＝3x2－x－＋cos x·x－2＋(－2x－3)sin x ‎＝3x2－＋－.‎ ‎∴y′＝3x2＋－－.‎ ‎(2)∵y＝＋ ‎＝＝－2，‎ ‎∴y′＝(－2)′＝＝.‎ ‎(3)y′＝(＋)′＝()′＋()′‎ ‎＝＋ ‎＝ ‎＝.‎ ‎(4)∵y＝1－sin2 ‎＝(3＋1－2sin2)‎ ‎＝(3＋cos x)＝＋cos x，‎ ‎∴y′＝(＋cos x)′＝－sin x.‎ 反思与感悟　对较复杂的式子进行化简变形对求导十分必要，否则将增大计算量甚至导致错误．如题中(1)、(2)、(4)变形后求导很方便．‎ 跟踪训练1　求下列函数的导数：‎ ‎(1)y＝x·tan x；‎ ‎(2)y＝；‎ ‎(3)y＝xsin x－.‎ 解　(1)y′＝(x·tan x)′＝()′‎ ‎＝ ‎＝＝.‎ ‎(2)y′＝ ‎＝.‎ ‎(3)y′＝(xsin x)′－()′‎ ‎＝sin x＋xcos x－.‎ 探究点二　导数的应用 例2　(1)曲线y＝xex＋2x＋1在点(0,1)处的切线方程为 ．‎ 答案　3x－y＋1＝0‎ 解析　y′＝ex＋xex＋2，则曲线在点(0,1)处的切线的斜率为k＝e0＋0＋2＝3，所以所求切线方程为y－1＝3x，即3x－y＋1＝0.‎ ‎(2)在平面直角坐标系xOy中，点P在曲线C：f(x)＝x3－10x＋3上，且在第二象限内，已知曲线C在点P处的切线斜率为2，则点P的坐标为 ．‎ 答案　(－2,15)‎ 解析　设P(x0，y0)(x0<0)，‎ 由题意知，f′(x0)＝3x－10＝2，‎ ‎∴x＝4.∴x0＝－2，∴y0＝15.‎ ‎∴P点的坐标为(－2,15)．‎ ‎(3)已知某运动着的物体的运动方程为s(t)＝＋2t2(位移单位：m，时间单位：s)，求t＝3 s时物体的瞬时速度．‎ 解　∵s(t)＝＋2t2＝－＋2t2＝－＋2t2，‎ ‎∴s′(t)＝－＋2·＋4t，‎ ‎∴s′(3)＝－＋＋12＝，‎ 即物体在t＝3 s时的瞬时速度为 m/s.‎ 反思与感悟　本题应用导数的运算法则进一步强化导数的物理意义及几何意义：函数y＝f(x)在点x0处的导数就是曲线y＝f(x)在点P(x0，y0)处的切线的斜率，即k＝f′(x0)；瞬时速度是位移函数s(t)对时间t的导数，即v＝s′(t)．‎ 跟踪训练2　(1)曲线f(x)＝－在点M处的切线的斜率为(　　)‎ A．－ B. C．－ D. 答案　B 解析　∵f′(x)＝ ‎＝，‎ ‎∴f′()＝，‎ ‎∴曲线在点M处的切线的斜率为.‎ ‎(2)设函数f(x)＝x3－x2＋bx＋c，其中a>0，曲线y＝f(x)在点P(0，f(0))处的切线方程为y＝1，确定b、c的值．‎ 解　由题意得，f(0)＝c，f′(x)＝x2－ax＋b，‎ 由切点P(0，f(0))既在曲线f(x)＝x3－x2＋bx＋c上又在切线y＝1上知，‎ 即，故b＝0，c＝1.‎ ‎1．设y＝－2exsin x，则y′等于(　　)‎ A．－2excos x B．－2exsin x C．2exsin x D．－2ex(sin x＋cos x)‎ 答案　D 解析　y′＝－2(exsin x＋excos x)＝－2ex(sin x＋cos x)．‎ ‎2．函数y＝的导数是(　　)‎ A. B. C. D. 答案　C 解析　y′＝′＝ ‎＝.‎ ‎3．曲线f(x)＝在点(－1，－1)处的切线方程为(　　)‎ A．y＝2x＋1 B．y＝2x－1‎ C．y＝－2x－3 D．y＝－2x＋2‎ 答案　A 解析　∵f′(x)＝＝，‎ ‎∴k＝f′(－1)＝＝2，‎ ‎∴切线方程为y＋1＝2(x＋1)，即y＝2x＋1.‎ ‎4．直线y＝x＋b是曲线y＝ln x(x>0)的一条切线，则实数b＝ .‎ 答案　ln 2－1‎ 解析　设切点为(x0，y0)，∵y′＝，∴＝，‎ ‎∴x0＝2，∴y0＝ln 2，ln 2＝×2＋b，‎ ‎∴b＝ln 2－1.‎ ‎[呈重点、现规律]‎ 求函数的导数要准确把函数分割为基本函数的和、差、积、商，再利用运算法则求导数．在求导过程中，要仔细分析出函数解析式的结构特征，根据导数运算法则，联系基本函数的导数公式．对于不具备导数运算法则结构形式的要适当恒等变形，转化为较易求导的结构形式，再求导数，进而解决一些切线斜率、瞬时速度等问题．‎ 一、基础过关 ‎1．设f(x)＝xln x，若f′(x0)＝2，则x0的值为(　　)‎ A．e2 B．e C. D．ln 2‎ 答案　B 解析　由f(x)＝xln x得f′(x)＝ln x＋1.‎ 根据题意知ln x0＋1＝2，所以ln x0＝1，因此x0＝e.‎ ‎2．已知函数f(x)＝x2＋4ln x，若存在满足1≤x0≤3的实数x0，使得曲线y＝f(x)在点(x0，f(x0))处的切线与直线x＋my－10＝0垂直，则实数m的取值范围是(　　)‎ A．[5，＋∞) B．[4,5]‎ C．[4，] D．(－∞，4)‎ 答案　B 解析　f′(x)＝x＋，当1≤x0≤3时，f′(x0)∈[4,5]，‎ 又k＝f′(x0)＝m，所以m∈[4,5]．‎ ‎3．设曲线y＝在点(3,2)处的切线与直线ax＋y＋1＝0垂直，则a等于(　　)‎ A．2 B. C．－ D．－2‎ 答案　D 解析　∵y＝＝1＋，‎ ‎∴y′＝－.∴y′|x＝3＝－.‎ ‎∴－a＝2，即a＝－2.‎ ‎4．已知曲线y＝x3在点P处的切线斜率为k，则当k＝3时P点坐标为(　　)‎ A．(－2，－8) B．(－1，－1)或(1,1)‎ C．(2,8) D．(－，－)‎ 答案　B 解析　y′＝3x2，∵k＝3，‎ ‎∴3x2＝3，∴x＝±1，‎ 则P点坐标为(－1，－1)或(1,1)．‎ ‎5．在平面直角坐标系xOy中，若曲线y＝ax2＋(a，b为常数)过点P(2，－5)，且该曲线在点P处的切线与直线7x＋2y＋3＝0平行，则a＋b的值是 ．‎ 答案　－3‎ 解析　y＝ax2＋的导数为y′＝2ax－，‎ 直线7x＋2y＋3＝0的斜率为－.‎ 由题意得解得 则a＋b＝－3.‎ ‎6．已知f(x)＝x3＋3xf′(0)，则f′(1)＝ .‎ 答案　1‎ 解析　f′(x)＝x2＋3f′(0)，‎ 令x＝0，则f′(0)＝0，‎ ‎∴f′(1)＝12＋3f′(0)＝1.‎ ‎7．求下列函数的导数：‎ ‎(1)y＝(2x2＋3)(3x－1)；(2)y＝(－2)2；‎ ‎(3)y＝x－sin cos .‎ 解　(1)方法一　y′＝(2x2＋3)′(3x－1)＋(2x2＋3)(3x－1)′‎ ‎＝4x(3x－1)＋3(2x2＋3)＝18x2－4x＋9.‎ 方法二　∵y＝(2x2＋3)(3x－1)‎ ‎＝6x3－2x2＋9x－3，‎ ‎∴y′＝(6x3－2x2＋9x－3)′＝18x2－4x＋9.‎ ‎(2)∵y＝(－2)2＝x－4＋4，‎ ‎∴y′＝x′－(4)′＋4′＝1－4·x－＝1－2x－.‎ ‎(3)∵y＝x－sin cos ＝x－sin x，‎ ‎∴y′＝x′－(sin x)′＝1－cos x.‎ 二、能力提升 ‎8．若函数f(x)＝ax4＋bx2＋c满足f′(1)＝2，则f′(－1)等于(　　)‎ A．－1 B．－2 C．2 D．0‎ 答案　B 解析　f′(x)＝4ax3＋2bx，‎ ‎∵f′(x)为奇函数且f′(1)＝2，‎ ‎∴f′(－1)＝－2.‎ ‎9．当函数y＝(a>0)在x＝x0处的导数为0时，那么x0等于(　　)‎ A．a B．±a ‎ C．－a D．a2‎ 答案　B 解析　y′＝′＝＝，‎ 由x－a2＝0得x0＝±a.‎ ‎10．已知函数f(x)的导函数为f′(x)，且满足f(x)＝3x2＋2x·f′(2)，则f′(5)＝ .‎ 答案　6‎ 解析　对f(x)＝3x2＋2xf′(2)求导，‎ 得f′(x)＝6x＋2f′(2)．‎ 令x＝2，得f′(2)＝－12.‎ 再令x＝5，得f′(5)＝6×5＋2f′(2)＝6.‎ ‎11．求过点(2,0)且与曲线y＝x3相切的直线方程．‎ 解　点(2,0)不在曲线y＝x3上，可令切点坐标为(x0，x)．由题意，所求直线方程的斜率k＝＝y′|x＝x0＝3x，即＝3x，解得x0＝0或x0＝3.‎ 当x0＝0时，得切点坐标是(0,0)，斜率k＝0，则所求直线方程是y＝0；‎ 当x0＝3时，得切点坐标是(3,27)，斜率k＝27，‎ 则所求直线方程是y－27＝27(x－3)，‎ 即27x－y－54＝0.‎ 综上，所求的直线方程为y＝0或27x－y－54＝0.‎ ‎12．已知曲线f(x)＝x3－3x，过点A(0,16)作曲线f(x)的切线，求曲线的切线方程．‎ 解　设切点为(x0，y0)，‎ 则由导数定义得切线的斜率k＝f′(x0)＝3x－3，‎ ‎∴切线方程为y＝(3x－3)x＋16，‎ 又切点(x0，y0)在切线上，‎ ‎∴y0＝3(x－1)x0＋16，‎ 即x－3x0＝3(x－1)x0＋16，‎ 解得x0＝－2，‎ ‎∴切线方程为9x－y＋16＝0.‎ 三、探究与拓展 ‎13．设有抛物线C：y＝－x2＋x－4，过原点O作C的切线y＝kx，使切点P在第一象限．‎ ‎(1)求k的值；‎ ‎(2)过点P作切线的垂线，求它与抛物线的另一个交点Q的坐标．‎ 解　(1)设点P的坐标为(x1，y1)，则y1＝kx1，①‎ y1＝－x＋x1－4，②‎ ‎①代入②得x＋(k－)x1＋4＝0.‎ ‎∵P为切点，∴Δ＝(k－)2－16＝0得k＝或k＝.‎ 当k＝时，x1＝－2，y1＝－17.‎ 当k＝时，x1＝2，y1＝1.‎ ‎∵P在第一象限，∴所求的斜率k＝.‎ ‎(2)过P点作切线的垂线，其方程为y＝－2x＋5.③‎ 将③代入抛物线方程得x2－x＋9＝0.‎ 设Q点的坐标为(x2，y2)，即2x2＝9，‎ ‎∴x2＝，y2＝－4.‎ ‎∴Q点的坐标为(，－4)．‎